Blätterung

Die Blätterung (frz. feuilletages, eng. foliations) einer Mannigfaltigkeit ist ein Begriff aus dem mathematischen Teilgebiet der Differentialtopologie. Die topologische Theorie der Blätterungen wurde im Wesentlichen von Georges Reeb begründet.

Eine $2$-dimensionale Blätterung einer $3$-Mannigfaltigkeit kann man sich wie die Schichten von Schiefer vorstellen

Blätterteig hat ebenfalls annähernd eine Blätterungsstruktur.

Eine $k$-dimensionale Blätterung einer Mannigfaltigkeit ist eine Zerlegung $\mathcal{K}=\{K_\theta\}$ von $M$ in disjunkte, wegzusammenhängende Mengen, die lokal um jeden Punkt so aussehen, wie eine Schichtung paralleler $k$-dimensionaler Untermannigfaltigkeiten. Die Elemente $K_\theta$ nennt man die Blätter von $\mathcal{K}$; die Blätter sind nicht notwendigerweise abgeschlossen oder gar kompakt.

Definition

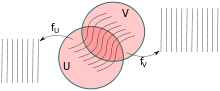
Sei $M$ eine einer glatte Mannigfaltigkeit. Eine Partition $\mathcal{K}=\{K_\theta\}$ von $M$ in disjunkte wegzusammenhängende Mengen heißt Blätterung von $M$, wenn ein Atlas $\mathcal{A} = \{(U_\eta,h_\eta)\}$ existiert (d.h. $\{U_\eta\}$ ist eine offene Überdeckung und die $h_\eta:\,U_\eta \to \R^n$ sind Diffeomorphismen), so dass das Bild jeder nichtleeren Zusammenhangskomponente von $K_\theta \cap U_\eta$ unter $h_\eta$ in eine $k$-Ebene $\R^k\times \{(x_{k+1},\dots,x_n)\} \subset \R^n$ abgebildet wird. Die Elemente $K_\theta$ nennt man die Blätter von $\mathcal{K}$

Beispiele

• Sei $X$ ein nichtverschwindendes Vektorfeld auf $M$, dann bilden die Flusslinien von $X$ eine eindimensionale Blätterung.
• Im Allgemeinen bilden Blätter global keine Untermannigfaltigkeit. Auf dem $2$-Torus $T^2 = \R^2 / \Z^2$ betrachte man das konstante Vektorfeld $(1,\sqrt{2})$. Jede Flusslinie windet sich dicht um den Torus. Somit stimmt die Topologie eines solchen Blattes nicht mit der Topologie von $\R^1$ überein (Dies ist auch ein Beispiel dafür, dass nicht jede Untergruppe einer Lie-Gruppe eine Liesche Untergruppe ist).
• Sei $p \colon M\to B$ ein Faserbündel, dann ist $\{K_b\}:=\{p^{-1}(b): b\in B\}$ eine Blätterung.
• Allgemeiner, sei $p \colon M\to B$ eine Submersion, dann ist $\{K_b\}:=\{p^{-1}(b): b\in B\}$ eine Blätterung. Ein Beispiel einer Submersion, die kein Faserbündel ist, ist $f(x,y)=(x^2-1)e^y$. Dies liefert eine Blätterung von $[-1,1]\times \R$, invariant unter der Translation $(x,y)\to(x,y+1)$, die induzierte Blätterung auf $[-1,1]\times S^1$ ist die 2-dimensionale orientierbare Reeb-Blätterung. Weiterhin ist die Blätterung auch invariant unter $(x,y)\to(-x,y+1)$, in diesem Fall ist die induzierte Blätterung auf dem Möbiusband die 2-dimensionale nicht-orientierbare Reeb-Blätterung.
• Sei $f \colon F\to F$ ein Homöomorphismus einer Mannigfaltigkeit F, dann hat der Abbildungstorus von f eine Blätterung transversal zu den Fasern, die sogenannte Suspensions-Blätterung.
• Die Hopf-Faserung ist eine Blätterung der $S^3$ in Kreise. Aus dem Satz von Vogt folgt, dass auch der $\mathbb R^3$ eine Blätterung in Kreise besitzt.

Satz von Frobenius

In obigen Beispielen wurde nicht direkt eine Partition $\mathcal{K}$ vorgegeben, sondern stattdessen wurde an jedem Punkt nur eine Richtung spezifiziert, und es stellte sich die Frage, ob es eine Blätterung gibt, so dass jedes Blatt an jedem Punkt tangential zur vorgegebenen Richtung ist. Häufig findet man in der Praxis ähnliche Situationen: Auf einer Mannigfaltigkeit $M$ ist eine $k$-dimensionale Distribution gegeben. Dies ist ein $k$-dimensionales Unterbündel des Tangentialraums. Ob es zu dieser Distribution eine Blätterung gibt, die tangential dazu liegt, lässt sich oft durch den Satz von Frobenius beantworten.

Die Lie-Klammer zweier Vektorfelder, die auf einer Mannigfaltigkeit definiert sind, ergibt wieder ein Vektorfeld auf dieser Mannigfaltigkeit. Da jedes Blatt $K_\theta$ einer Blätterung $\mathcal{K}=\{K_\theta\}$ lokal die Gestalt einer Untermannigfaltigkeit besitzt, folgt dann, dass für zwei beliebige Vektorfelder $X,Y$, die tangential zu $K_\theta$ sind (und die nur auf diesem Blatt definiert sein müssen) auch wieder $[X,Y]$ tangential zu $K_\theta$ ist. Der Satz von Frobenius impliziert hingegen auch die Rückrichtung.

Satz von Frobenius (nach Ferdinand Georg Frobenius): Zu einer $k$-dimensionalen Distribution $D$ existiert genau dann eine dazu tangentiale $k$-dimensionale Blätterung, wenn für beliebige Vektorfelder $X,Y$, die in $D$ liegen, deren Lie-Klammer $[X,Y]$ auch wieder einen Schnitt in $D$ bildet.

Eine topologische Obstruktion gegen die Integrabilität von Distributionen liefert der Satz von Bott.

Satz von Bott (nach Raoul Bott): Wenn eine $k$-dimensionale Distribution $D$ eine tangentiale $k$-dimensionale Blätterung besitzt, dann verschwindet der von den Pontrjagin-Klassen von $TM/D$ erzeugte Ring $Pont(TM/D)$ in Dimensionen $d>2(n-k)$.

Existenzsatz

Satz von Thurston (nach William Thurston): Eine geschlossene glatte n-dimensionale Mannigfaltigkeit hat genau dann eine glatte (n-1)-dimensionale Blätterung, wenn ihre Euler-Charakteristik Null ist. Wenn die Euler-Charakteristik Null ist, dann ist jedes (n-1)-dimensionale Hyperebenenfeld homotop zum Tangentialebenenfeld einer glatten Blätterung.

Blätterungen von Flächen

Wenn F eine geblätterte geschlossene Fläche ist, dann ist F entweder ein Torus oder eine Kleinsche Flasche und die Blätterung ist entweder die Suspensions-Blätterung eines Homöomorphismus $f:S^1\to S^1$ oder sie besteht aus mehreren (orientierbaren oder nicht-orientierbaren) Reeb-Blätterungen.

Blätterungen von 3-Mannigfaltigkeiten

Kodimension 1

Satz von Novikov-Zieschang (nach Sergei Nowikow und Heiner Zieschang): Wenn es auf einer geschlossenen, orientierbaren 3-Mannigfaltigkeit $M\not= S^2\times S^1$ eine 2-dimensionale Blätterung ohne Reeb-Komponenten gibt, dann ist $\pi_2(M)=0$ und alle Blätter sind inkompressibel.

Satz von Palmeira: Wenn es auf einer geschlossenen, orientierbaren 3-Mannigfaltigkeit $M\not= S^2\times S^1$ eine 2-dimensionale Blätterung ohne Reeb-Komponenten gibt, dann ist die universelle Uberlagerung diffeomorph zum $R^3$ und die hochgehobene Blätterung ist eine Blätterung des $R^3$ durch Blätter diffeomorph zum $R^2$.

Satz von Gabai (nach David Gabai): Sei M eine geschlossene, irreduzible 3-Mannigfaltigkeit mit $H_2(M)\not=0$, dann gibt es auf M eine 2-dimensionale Blätterung ohne Reeb-Komponenten.

Kodimension 2

Satz von Epstein (nach David Epstein): Jede Blätterung einer kompakten 3-Mannigfaltigkeit durch Kreise ist eine Seifert-Faserung.

Satz von Vogt (nach Elmar Vogt): Wenn eine 3-Mannigfaltigkeit $M$ eine Blätterung durch Kreise besitzt, dann trägt auch jede durch Entfernen endlich vieler Punkte aus $M$ entstandene Mannigfaltigkeit eine (nicht notwendig differenzierbare) Blätterung durch Kreise.

Literatur

• R. Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, Tensor Analysis and Applications., Springer-Verlag, Berlin 2003, ISBN 0-201-10168-8, Kap. 4.4