Dreiteilung des Winkels

Unter dem Problem der Dreiteilung des Winkels (auch: Trisektion des Winkels) versteht man in der Geometrie die Frage, ob man einen beliebigen Winkel mit Hilfe von Zirkel und Lineal (mit den euklidischen Werkzeugen) in drei gleich große Winkel unterteilen kann. Die Dreiteilung des Winkels gehört zu den drei klassischen Problemen der antiken Mathematik und ist nur für bestimmte Winkel durchführbar. Obwohl die Problemstellung der Winkeldreiteilung bis in die Antike zurückreicht, konnte erst im 19. Jahrhundert mit Methoden der Algebra gezeigt werden, dass sie mit Zirkel und Lineal im Allgemeinen nicht zu lösen ist.

Der erste Beweis dieser Negativaussage stammt von Pierre Wantzel aus dem Jahr 1837. In ihm wird das Problem auf eine algebraische Gleichung dritten Grades reduziert und argumentiert, dass deren Lösungen keine konstruierbaren Zahlen sind, sie sich also nicht in endlich vielen Schritten mit Zirkel und Lineal aus der Länge 1 konstruieren lassen. Um zu zeigen, dass es keine allgemeine Konstruktion für die Winkeldreiteilung gibt, reicht die Angabe eines einzigen Gegenbeispiels: Beispielsweise ist es nicht möglich, den konstruierbaren Winkel 60° zu dritteln, da 20° nicht konstruierbar ist. Es gibt jedoch auch Winkel, die mit Zirkel und Lineal nicht konstruiert, aber mit diesen Mitteln gedrittelt werden können (Näheres in Abzählbarkeit der Menge der drittelbaren Winkel), wenn sie zu Beginn gegeben sind.

Obwohl eine klassische Konstruktion nicht möglich ist, kann die Dreiteilung eines Winkels unter Zuhilfenahme von Hilfsmaterialien, wie eines markierten Lineals, als sogenannte Neusis-Konstruktion vollzogen werden. Einige dieser Techniken waren bereits in der Antike bekannt. In auffälligem Gegensatz zum Problem der Winkeldreiteilung steht die unter Verwendung der Winkelhalbierenden sehr leicht machbare Winkelhalbierung mit Zirkel und Lineal.

Klassisches Problem

Beispiele für drittelbare Winkel:
Für ein Drittel des Winkels 9° bedarf es z. B. zuerst der Winkel 30° und 18° um schließlich 3° zu erhalten (regelmäßiges Fünfeck).

Nach der klassischen Vorgabe zählt eine Lösung nur, wenn der gegebene Winkel allein mit Hilfe eines Zirkels und eines nichtskalierten Lineals in drei gleich große Teile aufgeteilt wird. Dies ist, wie bereits erwähnt, im Allgemeinen nicht möglich. Bei speziellen Winkeln ist eine Dreiteilung des Winkels mit den euklidischen Werkzeugen aber möglich, etwa bei jedem ganzzahligen Vielfachen von 9°.

Schon die alten Griechen versuchten vergeblich, eine allgemeine Lösung für beliebige Winkel zu finden. Um das Jahr 1830 schuf der französische Mathematiker Évariste Galois die Grundlagen des späteren Beweises dafür, dass dies nicht allgemein möglich ist. Warum dies unmöglich ist, wird im Abschnitt Beweis der Unmöglichkeit verdeutlicht.

Eine allgemeine Dreiteilung ist daher nur möglich, wenn neben Zirkel und Lineal auch zusätzliche Hilfsmittel Verwendung finden, etwa eine Trisektrix, oder wenn auf dem Lineal Markierungen angebracht werden. Andererseits sind mit Zirkel und Lineal beliebig gute Näherungslösungen darstellbar (siehe Abschnitt Näherungsverfahren).

Geschichte

Antike

Die Griechen waren es, die im 5. Jahrhundert v. Chr. das Problem, einen beliebigen Winkel in drei gleich große Winkel zu unterteilen, erkannten. Vermutlich trat dieses Problem in den Vordergrund mathematischen Interesses, als sie versuchten, für astronomische Zwecke eine Sehnentafel aufzustellen. Sie strebten nach einer Lösung, die allein mit Zirkel und einem unmarkierten Lineal – eine auf Oinopides von Chios (~ 440 v. Chr.) zurückgehende Beschränkung – zu bewältigen sei, aber sie fanden keine, die dieser Vorgabe gerecht wurde. Beispielsweise bei der Sehnentafel des Ptolemaios stößt man auf die elementargeometrisch nicht mehr zu bewältigende Aufgabe, aus der Sehne für $3^{\circ }$ die Sehne für $1^{\circ }$ zu gewinnen. Die für die Sehnengeometrie erforderliche Trigonometrie wurde viele Jahrhunderte bis Nikolaus Kopernikus (1473–1543) lediglich als Bestandteil der Astronomie aufgefasst und dementsprechend in astronomischen Werken behandelt. Das erste selbständige Lehrbuch der Trigonometrie verfasste Regiomontanus um 1464, doch erschien es erst posthum, fast 70 Jahre später, im Jahr 1533.

Hippias von Elis (um 460 bis um 400 v. Chr.) fand als Erster um 422 v. Chr. eine Lösung mithilfe eines sogenannten zusätzlichen Hilfsmittels. Es war eine Hilfskurve, sie wurde bekannt als die Trisektrix des Hippias oder Quadratrix des Hippias. Diese ist sogar für die Teilung eines Winkels in $n$ gleiche Teile erdacht. Der Name Quadratrix rührt daher, dass sie auch das Problem der Kreisquadratur beantwortet. Daraus kann gefolgert werden, dass es sich um eine transzendente Kurve handelt. Dennoch ist sie leicht beschreibbar, da sie durch zwei einfache Bewegungen erzeugt wird.

Archimedes von Syrakus (287 bis 212 v. Chr.) fand eine pragmatische Lösung. Obgleich die Zuweisung an Archimedes nicht gesichert ist, existiert eine nur auf Arabisch überlieferte Konstruktion des regelmäßigen Siebenecks. Während die regelmäßigen Drei-, Vier-, Fünf- und Sechsecke sich bekanntlich mit Zirkel und Lineal in einem gegebenen Kreis beschreiben lassen, geht das beim Siebeneck nicht mehr. Algebraisch führt die Teilung des Kreises in sieben gleiche Teile auf eine kubische Gleichung und gehört daher der gleichen Problemklasse an wie die Würfelverdoppelung und die Winkeldreiteilung. Die angeblich von Archimedes gefundene Konstruktion arbeitet zwar auch nur mit diesen beiden Geräten, verwendet das Lineal allerdings in einer in der euklidischen Geometrie nicht erlaubten Weise: Es wird so lange um einen festen Punkt gedreht, bis zwei Dreiecke, von denen eines bei der Drehung anwächst, während das andere abnimmt, flächengleich sind. Es ist dies ein besonderer Typus einer Einschiebekonstruktion oder sog. Neusis. Das angewandte Verfahren ist zwar von theoretischem Interesse, aber nicht praktisch verwendbar. Heute wird es als Neusis-Konstruktion bezeichnet. Später schuf Archimedes eine spezielle Kurve, nannte sie Spirale (archimedische Spirale) und untersuchte damit die Winkelteilung und die Quadratur des Kreises.

Im 2. Jh. v. Chr. ersann Nikomedes ein Instrument, das die Forderung der von Pappos überlieferten Neusis-Konstruktion mechanisch zu erfüllen gestattet. Die damit konstruierbaren Kurven erhielten wegen ihrer Gestalt den Namen Konchoide, auf Deutsch Muschelkurven. Das Instrument besteht aus zwei T-förmig fest miteinander verbundenen Linealen, auf denen sich ein drittes in bestimmter Weise bewegen kann. Es diente ihm damit als zusätzliches Hilfsmittel für die Dreiteilung des Winkels.

Pappos von Alexandria (im 4. Jh. n. Chr.) gehörte dem Kreis der alexandrinischen Neuplatoniker an. Seine Collectiones sind ein Sammelwerk in acht Büchern; bis auf das erste und den Anfang des zweiten sind sie allesamt erhalten geblieben. In der frühen Neuzeit entnahmen die europäischen Mathematiker den Collectiones viele Anregungen, enthalten sie doch wichtige Auszüge aus den Schriften von Euklid, Apollonios, Archimedes und anderen Mathematikern. Pappos erweiterte diese Auszüge um kritische Kommentare und teils eigene Ergänzungen. Er zeigte u. a. zwei unterschiedliche Varianten für die Lösung der Winkeldreiteilung mit Hilfsmitteln – eine pragmatische mit einem markierten Lineal als zusätzlichem Hilfsmittel, sprich eine Neusis-Konstruktion (siehe hierzu den Abschnitt Die Methode des Pappos) und eine zweite, in der er die Hyperbel als Trisektrix nutzte.

Früh- bis Spätmittelalter

Ahmad ibn Mûsâ lebte Mitte des 9. Jahrhunderts in Bagdad und war einer der drei Brüder, die sich Banū Mūsā nannten. Er war Astronom und Mathematiker. Seine Lösung zeigt zwei vorbestimmte Asymptoten einer Hyperbel, die durch einen gegebenen Punkt verläuft. Für die Drittelung des Winkels bedarf es eines markierten Lineals und somit einer Neusis-Konstruktion. Seine Lösung war der von Pappos’ Papierstreifenkonstruktion sehr ähnlich (siehe hierzu den Abschnitt Die Methode des Pappos).

Thabit ibn Qurra (826–901) aus Bagdad war anfangs Geldwechsler, fand Interesse an der Wissenschaft, wurde in Mathematik geschult und befasste sich auch mit Philosophie und Astronomie. Für seine Neusis-Konstruktion nutze er ebenfalls die Hyperbel. Seine Konstruktion war aber, im Gegensatz zu der von Ahmad ibn Mûsâ, exakter bezeichnet und ausführlicher begründet. Auch seine Lösung hatte große Ähnlichkeit mit Pappos Papierstreifenkonstruktion.

Ihren Höhepunkt erreichte die muslimische Astronomie und Trigonometrie im 15. Jahrhundert an der Sternwarte des Ulug Beg in Samarkand. Dort war al-Kaschi tätig, der sich eines geschickten Iterationsverfahrens bediente, um mit großer Genauigkeit aus der Winkeldreiteilungsgleichung den Sinus von $1^{\circ }$ zu berechnen. Im Prinzip ging er folgendermaßen vor. Da sich $\sin(3^{\circ })$ beliebig exakt bestimmen ließ (man konnte ihn z. B. aus der Differenz von $36^{\circ }$ am Fünfeck und $30^{\circ }$ am Sechseck mit Zirkel und Lineal konstruieren), verwendete er die Winkeldreiteilungsgleichung

$\sin(3\alpha )=3\sin(\alpha )-4\sin(\alpha )^{3}$.

In dieser trigonometrischen Schreibweise findet sie sich erstmals am Ende des 16. Jahrhunderts bei Vieta. Sie ist vom Typus $x^{3}+q=px$ (in der damaligen Klassifikation wurden die Koeffizienten – hier $p={\tfrac {3}{4}}$, $q={\tfrac {1}{4}}\sin(3^{\circ })$ – als positiv vorausgesetzt). Al-Kaschi berechnete die erste Näherung aus $x={\tfrac {q+x^{3}}{p}}\approx {\tfrac {q}{p}}$ zu $x_{1}={\tfrac {q}{p}}$. Die zweite Näherung folgt dann analog aus $x_{2}={\tfrac {q+x_{1}^{3}}{p}}$ usw., wobei sich als Besonderheit ergibt, dass sich mit jedem Schritt eine weitere Sexagesimalstelle exakt ermitteln lässt. Das Ergebnis al-Kaschis, in Dezimalschreibweise umgerechnet, liefert 18 Stellen:

$\sin(1^{\circ })=0{,}\,017\,452\,406\,437\,283\,571\,\dots$

Eine große Anzahl arabischer Handschriften befindet sich noch ungesichtet in orientalischen Bibliotheken, so dass die Forschung bisher kein vollständiges Bild der Entwicklung und des erreichten Wissens erarbeiten konnte.

Renaissance bis Neuzeit

Albrecht Dürer steuerte als Mathematiker ebenfalls zur Theorie der Winkeldreiteilung bei. Neben guten Näherungskonstruktionen für das reguläre 7-, 9-, 11- und 13-Eck finden sich im 2. Buch seiner Underweysung auch die näherungsweise Winkeldreiteilung. Sie wurde 1931 mit mehreren anderen Näherungslösungen der gleichen Aufgabe verglichen und dabei wurde gezeigt, dass sie nirgends um mehr als etwa 20 Bogensekunden vom genauen Wert abweicht und damit alle anderen späteren Lösungsvorschläge übertrifft. Dürers Konstruktionsidee lässt sich zudem leicht iterieren und liefert nach einigen Schritten eine sehr hohe Genauigkeit. Bei allem ist sich Dürer des grundlegenden Unterschiedes zwischen exakten, er nennt sie demonstrative, und Näherungslösungen, er nennt sie mechanice, jederzeit bewusst und hebt sich damit sogar von den meisten professionellen Mathematikern seiner Zeit ab.

Die erste Person, die den Nachweis der Unlösbarkeit des Problems – allein mit Zirkel und Lineal – erbrachte, war Pierre-Laurent Wantzel im Jahr 1837. Es wird von Historikern jedoch bezweifelt, dass Wantzel als Erster um einen Beweis wusste, da schon der junge Carl Friedrich Gauß sehr wahrscheinlich über einen solchen verfügt hat. Ein großer Teil seines 1801 erschienenen Werkes Disquisitiones arithmeticae ist der Frage gewidmet, welche Bedingungen eine Polynomgleichung erfüllen muss, um durch quadratische Radikale lösbar zu sein. Dort finden sich auch die nach Gauß benannten Sätze, mit deren Hilfe für die meisten klassischen Aufgaben die Unlösbarkeit mit Zirkel und Lineal nachgewiesen werden kann. Mit den von ihm entwickelten Techniken bewies Gauß zum Beispiel, dass sich das 17-Eck mit Zirkel und Lineal konstruieren lässt. Die Tatsache, dass Wantzel trotzdem von vielen Autoren als Urheber der Sätze genannt und zitiert wird, führen die Mathematikhistoriker Christoph Scriba und Peter Schreiber auf die „Kommunikationsschwierigkeiten“ der Wissenschaft des 19. Jahrhunderts zurück.

Beweis der Unmöglichkeit

Geschichte des Beweises

Es ist im Allgemeinen nicht möglich, die Dreiteilung des Winkels allein mit Zirkel und Lineal zu vollziehen

Pierre Wantzel veröffentlichte 1837 einen Beweis, dass es im Allgemeinen unmöglich ist, einen Winkel mit Zirkel und Lineal in drei gleiche Teile zu zerlegen. Sein Beweis benutzt, wenn man es in moderner Terminologie ausdrückt, Körpererweiterungen, wie sie in der abstrakten Algebra und insbesondere in der Galoistheorie behandelt werden. Wantzel veröffentlichte diese Ergebnisse früher als Galois (dessen Werk 1846 herauskam) und benötigte dabei nicht den Zusammenhang zwischen Körpererweiterungen und Gruppen, mit dem sich die Galoistheorie befasst. Sein Beweis beruhte auf folgenden algebraischen Überlegungen:

1. Im ersten Teil des Beweises argumentiert er, dass, wenn ein Konstruktionsproblem mit Lineal und Zirkel gelöst werden kann, „die Unbekannte des Problems durch die Lösung einer Reihe von quadratischen Gleichungen erhalten werden kann, deren Koeffizienten rationale Funktionen der Parameter $p,q,r,\dots$ des Problems und der Wurzeln der vorherigen Gleichungen sind“.

Mit der „Unbekannten des Problems“ ist dabei zum Beispiel die gesuchte Strecke $x=\cos(\alpha )$ gemeint.

2. Danach zeigte er, dass jede algebraische Zahl $x_{n}^{0}$, die Lösung der letzten Gleichung $x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0$ eines Systems

${\begin{aligned}&x_{1}^{2}+Ax_{1}+B=0\\&x_{2}^{2}+A_{1}x_{2}+B_{1}=0\\&\vdots \\&x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0\end{aligned}}$

ist, wobei die Koeffizienten $A_{m},B_{m}$ stets durch sukzessive Adjunktion im Körper $\mathbb {Q} (p,q,r,\dots ,x_{1}^{0},\dots ,x_{m}^{0})$ liegen, eine Polynomgleichung des Grades $2^{n}$ mit Koeffizienten in $\mathbb {Q} (p,q,r,\dots )$ löst. Dabei löst $x_{j}^{0}$ die Gleichung $x_{j}^{2}+A_{j-1}x_{j}+B_{j-1}=0$ und $p,q,r,\dots$ sind die gegebenen Parameter des Problems.

3. Wantzel wusste, dass jede algebraische Zahl Nullstelle eines Polynoms mit Grad einer Zweierpotenz ist, wenn diese hinreichend groß gewählt würde. Daher war sein Hauptresultat, zu zeigen, dass, wenn die Anzahl an benötigten Gleichungen zu einem Minimum reduziert würde, das resultierende Polynom irreduzibel über $\mathbb {Q} (p,q,r,\dots )$ ist.

Die Unmöglichkeit der Konstruktion folgt nun als Korollar aus den Sätzen 1 bis 3: Wäre, beginnend mit den Strecken 0, 1 und $\cos(3\alpha )$, die Dreiteilung eines Winkels $3\alpha$ mit Zirkel und Lineal möglich, so müsste $\cos(\alpha )$ Nullstelle eines irreduziblen Polynoms über $\mathbb {Q} (\cos(3\alpha ))$ sein, das als Grad eine Zweierpotenz hat. Das Polynom $4x^{3}-3x-\cos(3\alpha )$ ist im Allgemeinen irreduzibel über $\mathbb {Q} (\cos(3\alpha ))$, hat aber den Grad 3. Dies ist ein Widerspruch.

Es ist zu beachten, dass Wantzels Originalpublikation von dem Mathematikhistoriker Jesper Lützen als lückenhaft und schwer zu verstehen angesehen wird – dies betrifft vor allen Dingen den „Beweis“ des Hauptsatzes 3. Von Lützen wurden die Lücken im Nachhinein geschlossen und die Resultate, wie oben beschrieben, in moderner Fachsprache formuliert. Wantzels Beweis für die Unmöglichkeit, die Dreiteilung des Winkels und die Verdoppelung des Würfels mit Lineal und Zirkel zu konstruieren, war nach seiner Veröffentlichung im Jahr 1837 fast ein Jahrhundert lang vergessen. Laut Lützen waren dabei die „mangelnde Berühmtheit des Autors“, die „Tatsache, dass einige seiner Zeitgenossen das Ergebnis als bekannt oder sogar als bewiesen ansahen“, und dass „das Ergebnis zum Zeitpunkt seiner Veröffentlichung nicht als wichtiges mathematisches Ergebnis angesehen wurde“, die treibenden Gründe.

Algebraischer Beweis

Kennt man $\cos(\theta )$, $\sin(\theta )$ oder $e^{i\theta }$, so kann der Winkel $\theta$ konstruiert werden. Die Frage ist also, ob man zum Beispiel aus der Information $e^{3i\theta }$ mit Zirkel und Lineal die Zahl $e^{i\theta }$ konstruieren kann.

Dreiteilung des Winkels $360^{\circ }$ mittels der dritten Einheitswurzeln in der komplexen Zahlenebene

Das Problem der Konstruktion eines Winkels von gegebener Größe $\alpha$ ist äquivalent zur Konstruktion zweier Strecken, deren Längen im Verhältnis $\cos(\alpha )$ stehen. Die Lösung eines dieser beiden Probleme mit Zirkel und Lineal ergibt die Lösung des anderen. Mithilfe der Formel zum Kosinus des dreifachen Winkels

$\cos(3\alpha )=4\cos ^{3}(\alpha )-3\cos(\alpha )$

lässt sich eine algebraische Gleichung aufstellen, die die Werte $\cos(3\alpha )$ und $\cos(\alpha )$ in Verbindung bringt. Daraus folgt, dass das Problem der Winkeldreiteilung äquivalent dazu ist, eine bestimmte Strecke zu konstruieren, bei der das Verhältnis zwischen Streckenlänge und Längeneinheit gleich einer Lösung einer bestimmten kubischen Gleichung ist. Damit ist das ursprünglich geometrische Problem auf ein rein algebraisches Problem zurückgeführt. Zu beachten ist hierbei, dass neben den zu Beginn einer Konstruktion mit Zirkel und Lineal zur Verfügung stehenden Strecken 0 und 1 noch auf die Strecke $\cos(3\alpha )$ zugegriffen werden kann, da auch der Startwinkel $3\alpha$ bekannt ist. Dabei ist es insbesondere für die Fragestellung, ob $3\alpha$ zu $\alpha$ gedrittelt werden kann, unerheblich, ob $3\alpha$ selbst aus 0 und 1 mit Zirkel und Lineal hätte konstruiert werden können.

Die kubische Gleichung kann einfach aus der Formel von De Moivre für die komplexe Exponentialfunktion gefolgert werden. Nach der Eulerschen Formel gilt

$e^{i\alpha }=\cos(\alpha )+i\sin(\alpha )$

und durch beidseitiges Potenzieren mit 3 kann die Gleichung über einen Vergleich der Realteile und $(e^{i\alpha })^{3}=e^{3i\alpha }$ abgelesen werden. Dabei bezeichnet $i$ die imaginäre Einheit der komplexen Zahlen.

Im Detail kann der Beweis der Unmöglichkeit der Winkeldreiteilung über folgende Ideen aus der Algebra vollzogen werden. Es seien eine Menge $M$ von Punkten (komplexen Zahlen), die mindestens 0 und 1 enthält, und ein beliebiger Punkt $z$ gegeben. Es ist für diese Überlegungen von Wichtigkeit, dass die komplexen Zahlen als Ebene aufgefasst werden können – im Gegensatz dazu werden die reellen Zahlen schlicht als Gerade aufgefasst. Dann gilt, dass der Punkt $z$ genau dann mit Zirkel und Lineal aus den Punkten $M$ konstruierbar ist, wenn er in einem Körper $E\subset \mathbb {C}$ (dabei ist $\mathbb {C}$ der Körper der komplexen Zahlen) liegt, der durch Adjunktion einer Quadratwurzel aus dem Körper

$K:=\mathbb {Q} (M\cup {\overline {M}})\subset \mathbb {C}$

hervorgeht. Dabei ist grob gesprochen $\mathbb {Q} (M\cup {\overline {M}})$ die Menge, die durch Bilden aller Summen, Differenzen, Produkte und Quotienten aus rationalen Zahlen mit $M\cup {\overline {M}}$ entsteht. Hier ist ${\overline {M}}=\{{\overline {m}}\mid m\in M\}$ die Menge der komplex Konjugierten aller Elemente von $M$ und das Symbol $\cup$ steht für die Vereinigung zweier Mengen. Adjunktion einer Quadratwurzel bedeutet, dass es ein $w^{2}\in K$ geben muss, so dass $E=K(w)$. Zum Beispiel geht $\mathbb {Q} ({\sqrt {2}})$ durch die Adjunktion einer Quadratwurzel aus den rationalen Zahlen hervor, da $({\sqrt {2}})^{2}=2$ eine rationale Zahl ist – entsprechend ist $\mathbb {Q} ({\sqrt {2}})$ die Menge aller Summen, Differenzen, Produkte und Quotienten rationaler Zahlen mit der Zahl ${\sqrt {2}}$. Bei $E\mid K$ handelt es sich um eine sogenannte Körpererweiterung. Das Problem der Winkeldreiteilung mittels Zirkel und Lineal lässt sich also auf die Frage reduzieren, ob die Zahl $\cos(\alpha )$ in einem Teilkörper von $\mathbb {C}$ liegt, der aus $\mathbb {Q} (\cos(3\alpha ))$ durch sukzessive Adjunktion von Quadratwurzeln gewonnen werden kann. Das bedeutet jedoch, dass der Erweiterungsgrad von $E$ aus $\mathbb {Q}$ eine Potenz von 2 sein muss. Es ist aber im Allgemeinen

$[\mathbb {Q} (\cos(\alpha ),\cos(3\alpha )):\mathbb {Q} (\cos(3\alpha ))]=3\not =2^{n}\qquad {\text{für alle}}\,n\in \mathbb {N} ,$

womit es unmöglich ist, die Winkeldreiteilung mittels Zirkel und Lineal vorzunehmen. Dass die Körpererweiterung $\mathbb {Q} (\cos(\alpha ),\cos(3\alpha ))\mid \mathbb {Q} (\cos(3\alpha ))$ im Allgemeinen vom Grad 3 ist, kann wie folgt gesehen werden: Wäre das Polynom $p(x)=4x^{3}-3x-\cos(3\alpha )$ für $3\alpha ={\tfrac {\pi }{3}}$ reduzibel über den rationalen Zahlen, müsste es eine rationale Nullstelle besitzen. Wegen $\cos({\tfrac {\pi }{3}})={\tfrac {1}{2}}$ kann äquivalenterweise $8x^{3}-6x-1=0$ studiert werden. Nach dem Satz über rationale Nullstellen kommen nur die Werte $\pm 1$, $\pm {\tfrac {1}{2}}$, $\pm {\tfrac {1}{4}}$ und $\pm {\tfrac {1}{8}}$ als rationale Nullstellen dieser Gleichung in Frage. Alle diese Werte können durch Einsetzen als Nullstelle ausgeschlossen werden. Somit muss $p(x)$ irreduzibel über $\mathbb {Q} (\cos({\tfrac {\pi }{3}}))=\mathbb {Q} ({\tfrac {1}{2}})=\mathbb {Q}$ sein, und das Minimalpolynom von $\cos({\tfrac {\pi }{9}})$ über $\mathbb {Q}$ hat den Grad 3.

Es kann gezeigt werden, dass sich der Winkel $\vartheta$ nicht mit Zirkel und Lineal dreiteilen lässt, falls $e^{i\vartheta }$ eine transzendente Zahl ist.

Winkel, für die die Dreiteilung mit Zirkel und Lineal möglich ist, werden als drittelbare Winkel bezeichnet.

Abzählbarkeit der Menge der drittelbaren Winkel

Es sei im Einheitskreis der Winkel $3\alpha$ mit $\cos(3\alpha )=1-{\tfrac {3}{2}}{\sqrt[{3}]{2}}$ gegeben, dann gilt $\cos(\alpha )=-\left({\tfrac {1}{3}}\left(1-{\tfrac {3}{2}}{\sqrt[{3}]{2}}\right)-{\tfrac {1}{3}}\right)={\tfrac {1}{2}}{\sqrt[{3}]{2}}$

Wie oben gesehen, ist der Winkel ${\tfrac {\pi }{3}}$, also 60°, zwar konstruierbar, aber nicht drittelbar. Allgemein können die zueinander unabhängigen Eigenschaften konstruierbar und drittelbar auf vier verschiedene Weisen kombiniert werden, und es stellt sich die Frage, wie häufig jeder Fall auftritt. Es wird damit nach der Wahrscheinlichkeit gefragt, mit der diese vier Fälle für zufällig gewählte Winkel eintreffen.

1. Der Winkel $3\alpha$ ist konstruierbar und drittelbar. Dann ist der Winkel $\alpha$ ebenfalls konstruierbar (und zwar auch ohne $3\alpha$ zu verwenden). Beispiele: Vielfache von 9° (siehe Grafik in Klassisches Problem).
2. Der Winkel $3\alpha$ ist konstruierbar, aber nicht drittelbar (der Winkel $\alpha$ ist dann nicht konstruierbar). Beispiel: 60° (wie gerade gezeigt).
3. Der Winkel $3\alpha$ ist nicht konstruierbar, aber drittelbar (der Winkel $\alpha$ ist dann ohne Verwendung von $3\alpha$ nicht konstruierbar, mit aber schon). Beispiel (siehe Grafik rechts): Winkel $3\alpha$ mit $\cos(3\alpha )=1-{\tfrac {3}{2}}{\sqrt[{3}]{2}}$.
4. Der Winkel $3\alpha$ ist weder konstruierbar, noch drittelbar (der Winkel $\alpha$ ist dann nicht konstruierbar, auch nicht unter Verwendung von $3\alpha$). Beispiele: Jeder Winkel $3\alpha$, für den $\cos(3\alpha )$ transzendent ist (siehe Algebraischer Beweis).

Um abzuschätzen, wie häufig die jeweiligen Fälle auftreten, kann die Mächtigkeit der vier Winkelklassen untersucht werden. Die ersten drei Klassen liefern nur abzählbar viele Winkel. Für die ersten beiden Klassen folgt dies unmittelbar: Jede konstruierbare Zahl ist algebraisch und daher gibt es nur abzählbar viele konstruierbare Zahlen. Es ist jedoch im dritten Fall nicht sofort klar, dass für jeden drittelbaren Winkel $3\alpha$ die Zahl $\cos(3\alpha )$ immer algebraisch ist. Da aber Winkel $3\alpha$ mit transzendentem $\cos(3\alpha )$ nicht drittelbar sind (4. Fall), folgt die Algebraizität von $\cos(3\alpha )$ im Umkehrschluss.

Der Kosinus jedes drittelbaren Winkels ist also algebraisch und daher gibt es nur abzählbar viele drittelbare Winkel. Im Gegensatz dazu enthält die vierte Klasse überabzählbar viele Winkel (da es überabzählbar viele transzendente Zahlen im Intervall $[-1,1]$ gibt). Ein zufällig gewählter Winkel kann also fast sicher mit Zirkel und Lineal nicht gedrittelt werden. Dennoch liegen sowohl drittelbare, als auch nicht drittelbare Winkel in $[0,2\pi ]$ dicht. Es gibt also in beliebig kleinen Umgebungen eines jeden Winkels sowohl drittelbare, als auch nicht drittelbare Winkel. Um das zu zeigen, reichen bereits Winkel der Form $n\pi /2^{k}$ für natürliche Zahlen $k$ und $n$ (für drittelbare Winkel) und Winkel der Form $n\pi /2^{k}+\pi /3$ (für nicht drittelbare Winkel).

Verallgemeinerung

Es sei der Zentriwinkel eines Vierzehnecks als $3\alpha ={\tfrac {\pi }{7}}$ gegeben, dann gilt $\alpha ={\tfrac {\pi }{7\cdot 3}}={\tfrac {\pi }{21}}={\tfrac {\pi }{3}}-2{\tfrac {\pi }{7}}$

Die allgemeinere Frage, für welche natürliche Zahlen $n>1$ die $n$-Teilung beliebiger Winkel möglich ist, hat keine überraschende Antwort: Es gibt nur die fortgesetzte Winkelhalbierung als allgemeines $n$-Teilungsverfahren und daher muss $n$ eine Zweierpotenz sein (Beispiel: dreimaliges Halbieren eines Winkels ergibt die Achtelung des Winkels). Das kann man wie folgt einsehen: Wenn es ein allgemeines Verfahren für ein $n$ gibt, das einen Primfaktor > 2 hat, dann könnte man den Vollkreis durch zweimaliges Anwenden des Verfahrens in $n^{2}$ gleiche Winkel aufteilen und so ein regelmäßiges Polygon mit $n^{2}$ Ecken konstruieren. Das widerspricht aber der Bedingung für konstruierbare regelmäßige Polygone (die Primteiler > 2 dürfen jeweils nur einmal vorkommen). Daher hat $n$ keinen Primfaktor > 2 und muss eine Zweierpotenz sein.

Für Winkel dieser Art gibt es auch ein allgemeines Ergebnis: ${\tfrac {2\pi }{N}}$ ($N$ für Eckenanzahl eines Vielecks) lässt sich genau dann in $n$ gleich große Winkel teilen, wenn $n$ das Produkt einer Zweierpotenz und paarweise verschiedener Fermatscher Primzahlen ist, die $N$ nicht teilen. Man kann also beispielsweise (siehe Grafik rechts) den zu Beginn gegebenen Zentriwinkel ${\tfrac {\pi }{7}}$ eines regelmäßigen Vierzehnecks mit Zirkel und Lineal in $3$, in $5$ und auch in $17$ gleich große Winkel teilen.

Lösungsversuche durch Amateure

Obwohl also die Unmöglichkeit der Dreiteilung eines beliebigen Winkels allein mit Zirkel und Lineal schon lange bekannt ist, werden bis in die Gegenwart mathematische Zeitschriften und Fakultäten mit Beweisversuchen von Amateuren überhäuft. Underwood Dudley, der das Phänomen analysierte, beschreibt den typischen Trisektor als älteren Mann, der in seiner Jugend von dem Problem hörte (es ist von den drei klassischen Problemen wahrscheinlich das für Laien zugänglichste) und im Ruhestand daran tüftelte. Dudley, der hunderte ihrer Beweisversuche sammelte, fand nur zwei Frauen unter den Winkeldreiteilern.

Ein weiteres Kennzeichen sei, so Dudley, dass Laien die Bedeutung von „unmöglich“ in der Mathematik nicht verstünden und dies stattdessen eher als Herausforderung sähen. Typischerweise hätten sie nur geringe Mathematikkenntnisse, dies müsse aber nicht unbedingt heißen, dass die Fehler in ihren Konstruktionen einfach zu finden sind. Charakteristischerweise seien ihre Diagramme sehr komplex, könnten aber mit geometrischen Kenntnissen häufig drastisch vereinfacht werden. Des Weiteren seien sie von der Wichtigkeit ihrer Lösungen für technische Anwendungen überzeugt, was wiederum für viele Patent- und Geheimhaltungsfragen nicht unwichtig ist.

Nachdem Dudley viele Methoden im Umgang mit hartnäckigen Winkeldreiteilern ausprobiert hatte, empfahl er, deren Arbeit als Beitrag zu einer besseren Näherungslösung an das Problem zu loben (wahlweise für deren Einfachheit oder Eleganz). Darüber hinaus soll man ihnen einen Computerausdruck, der den Fehler des Versuchs für verschiedene Winkel aufzeigt, zukommen lassen sowie Beispiele von „Näherungslösungen“ anderer Winkeldreiteiler.

Nichtklassische Verfahren

Beschränkt man sich nicht auf die klassischen Konstruktionvorschriften für Zirkel und Lineal, sondern lässt darüber hinaus die Verwendung anderer Konstruktionswerkzeuge und mathematischer Hilfsobjekte zu oder begnügt sich auch mit Näherungslösungen, so ergibt sich eine Vielzahl von möglichen Verfahren, einen beliebigen Winkel dreizuteilen. In den folgenden Abschnitten werden einige von ihnen beispielhaft vorgestellt.

Die Methode des Archimedes

Erforderlicher Anlegevorgang der Konstruktion

Archimedes war ein Pragmatiker, er gab zwar eine Lösung in seinem Liber Assumptorum an, aber er und ebenso die nachfolgenden Autoren ließen in den Überlieferungen seiner Werke die Vorgehensweise der sogenannten Einschiebung (Neusis) offen.

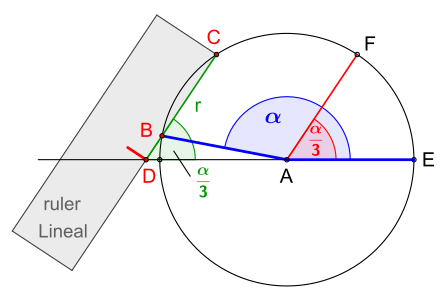
Es sei $\alpha$ der dreizuteilende Winkel wie in nebenstehender Zeichnung. Gehe dann wie folgt vor:

1. Schlage einen Halbkreis um $A$ mit beliebigem Radius $r$.
2. Am Lineal bringe zwei Markierungen im Abstand $r$ an.
3. Lege das Lineal so an $B$, dass eine der beiden Markierungen auf der Geraden $AD$ im Punkt $D$ und die andere auf der Kreislinie im Punkt $C$ liegt, und zeichne die Strecke ${\overline {BD}}$ bzw. ${\overline {CD}}$.
4. Der Winkel $\beta$ bei $D$ ist der gesuchte Drittelwinkel.

• 
  Anlegen des Lineals für Winkelweiten
  $135^{\circ }<\alpha <180^{\circ }$, ${\overline {AF}}$ ist parallel zu ${\overline {CD}}$
• 
  Anlegen des Lineals für
  $180^{\circ }<\alpha <270^{\circ }$, ${\overline {AF}}$ ist parallel zu ${\overline {CD}}$
• 
  Anlegen des Lineals für
  $\alpha >270^{\circ }$, ${\overline {AF}}$ ist parallel zu ${\overline {CD}}$
• 
  Beweisführung für die Winkeldreiteilung nach Archimedes: $\alpha =3\beta$

Zur Begründung beachte man, dass wegen der speziellen Positionierung des Lineals die Länge der Strecke ${\overline {CD}}$ gleich dem Abstand $r$ der Markierungen ist, also gleich dem Radius des Kreises, der sich auch als ${\overline {AC}}$ und ${\overline {AB}}$ wiederfindet. Insbesondere ist das Dreieck $ACD$ gleichschenklig, weshalb der Winkel $\beta$ auch bei $A$ auftritt. Der Winkel des Dreiecks $ACD$ bei $C$ ist einerseits gleich $180^{\circ }-2\beta$ (Winkelsumme im Dreieck), andererseits der Nebenwinkel von $\gamma$, also ist $\gamma =2\beta$. Da das Dreieck $ABC$ ebenfalls gleichschenklig ist, taucht der Winkel $\gamma$ auch bei $B$ auf, und der Winkel dieses Dreiecks bei $A$ ist gleich $180^{\circ }-2\gamma$. Beachtet man nun, dass sich die Winkel bei $A$ zu $180^{\circ }$ addieren, ergibt sich $\alpha =180^{\circ }-(180^{\circ }-2\gamma )-\beta =2\gamma -\beta =4\beta -\beta =3\beta$.

Dass mit dieser Methode jeder Winkel wie bewiesen dreigeteilt werden kann, steht nicht in Widerspruch zur Unlösbarkeit des klassischen Problems, denn die obige Konstruktion wurde nicht nach den klassisch geforderten Regeln durchgeführt. Eine Markierung am Lineal und ein geschicktes Anlegen des Lineals entsprechen keinen klassischen Konstruktionsmethoden. Es wurde also ein abweichender Instrumentensatz verwendet und die möglichen Konstruktionen sind vom Instrumentensatz abhängig.

Die Methode des Pappos

Methode des Pappos, Neusis-Konstruktion

Aus dem späten Altertum stammt die im Folgenden beschriebene Neusis-Konstruktion des Pappos zur Dreiteilung spitzer Winkel.

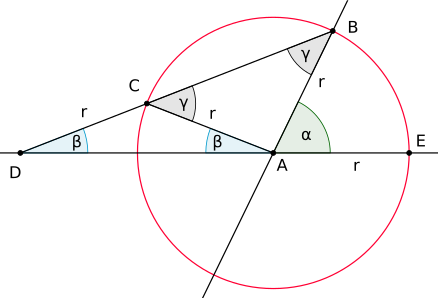
Zu teilen sei der Winkel $\angle {BAD}=3\alpha$, vgl. die rechte Abbildung:

Nach dem Zeichnen der beiden Winkelschenkel ${\overline {AB}}$ und ${\overline {AD}}$ wird eine beliebige Länge $a$ als Strecke ${\overline {AC}}$ auf dem Schenkel ${\overline {AD}}$ bestimmt. Eine Parallele zu ${\overline {AB}}$ ab $C$ sowie das Lot ab $C$ mit Fußpunkt $E$ auf ${\overline {AB}}$ schließen sich an. Nun wird das Lineal, auf dem die Länge gleich $2a$ markiert ist, so lange verschoben, bis der Eckpunkt $G$ auf der Parallelen zu ${\overline {AB}}$ liegt, die Länge $2a$ die Strecke ${\overline {CE}}$ in $F$ schneidet und dabei die Kante des Lineals durch den Scheitel $A$ verläuft. Der so gefundene Winkel $\angle {BAG}$ ist der gesuchte Winkel $\alpha .$

Denn dieser Winkel $\angle BAG=:\beta$ ist als Wechselwinkel gleich $\angle AGC=\angle FGC,$ dem Umfangswinkel der Kreissehne ${\overline {CF}},$ und nach dem Kreiswinkelsatz ist der zugehörige Mittelpunktswinkel $\angle FMC$ gleich $2\beta .$ Weil das Dreieck $\triangle AMC$ gleichschenklig ist, gilt auch $\angle FAC=2\beta .$ Dieser Winkel ist aber gleich der Differenz $\angle BAD-\angle BAG=3\alpha -\beta ,$ also gilt $2\beta =3\alpha -\beta$ und daraus folgt $\beta =\alpha .$

Die gestrichelten Linien und der Mittelpunkt $M$ sind für die Konstruktion nicht erforderlich, sie dienen lediglich der Beweisführung.

Teilung mit Tomahawk

Der Tomahawk ist eine Figur, die aus mathematischer Sicht aus zwei aufeinander senkrecht stehenden Strecken und einem an einer der Geraden anliegenden Halbkreis besteht; das hintere Ende ist dabei so lang wie der Radius des Halbkreises (siehe Zeichnung). Die Bezeichnung Tomahawk rührt daher, dass die Figur vage an einen Tomahawk (eine indianische Streitaxt) erinnert. Um einen Winkel mit Hilfe des Tomahawks dreizuteilen, muss man ihn so positionieren (siehe Bild 1), dass sein „Stiel“ (Griff des Tomahawks) durch den Winkelscheitel geht, während der Halbkreis (die Klinge des Tomahawks) und der „Haken“ (die hintere Spitze des Tomahawks) jeweils die Schenkel des Winkels berühren. In dieser Position bildet der Stiel mit einem der Schenkel einen Winkel, der genau ein Drittel des Ausgangswinkels beträgt. Die Verbindung des Mittelpunktes des Halbkreises mit der Winkelspitze teilt das zweite und dritte Drittel des Ausgangswinkels. Da der Tomahawk eine Figur ist, die angelegt werden muss, ist diese Methode nicht mit den klassischen Konstruktionsregeln (Lineal und Zirkel) konform.

Ist eine direkte Dreiteilung eines Winkels mithilfe eines Tomahawks nicht möglich, weil der gegebene Winkel zu klein ist, um den Tomahawk positionieren zu können, so lässt sich die Dreiteilung des kleinen Winkels aus der Dreiteilung des zugehörigen großen Nebenwinkels konstruieren. Betrachtet man einen Winkel $\alpha$ mit seinem Nebenwinkel an einem Halbkreis mit Radius $r$, so erhält man wegen ${\tfrac {2}{3}}(180^{\circ }-\alpha )+{\tfrac {2}{3}}\alpha =120^{\circ }$ einen konstanten Winkel, der nicht von der Größe des Winkels $\alpha$ abhängt (siehe Bild 3). Dieser $120^{\circ }$-Winkel ist Bestandteil eines gleichschenkligen Dreiecks, dessen Höhe ${\tfrac {r}{2}}$ beträgt. Damit ergibt sich dann die im nächsten Absatz beschriebene Konstruktion.

Es beginnt (siehe Bild 4) mit dem Einzeichnen des Durchmessers ${\overline {AB}}$, dessen Halbierung in $O$ und dem Ziehen des Halbkreises über ${\overline {AB}}$. Es folgt das Eintragen des gegebenen Winkels $\angle BOC$ mit seinen beiden Winkelschenkeln. Nun wird der Tomahawk folgendermaßen positioniert: der „Haken“ liegt auf der Strecke ${\overline {AO}},$ der Halbkreis berührt den oberen Winkelschenkel und der „Stiel“ verläuft durch den Mittelpunkt $O.$ Mit dem Einzeichnen der beiden Strecken ${\overline {DO}}$ und ${\overline {EO}}$ erhält man die Dreiteilung des Supplementwinkels $\angle {COA}$. Um eine Dreiteilung des Winkels $\angle BOC$ zu erzielen, wird nun der Punkt $E$ auf den Kreisbogen $OBC$ gespiegelt. Hierzu wird der Radius ${\overline {AO}}$ in $F$ halbiert und ein Halbkreis um $O$ ab $F$ gezogen, daraus ergibt sich der Schnittpunkt $G$. Abschließend bedarf es noch eines Halbkreises um $G$ mit Radius ${\overline {GO}}$, des Schnittpunktes $H$ und der geraden Linie ab $E$ durch $H$ bis zum Kreisbogen $OBC$. Der so erzeugte Schnittpunkt $E'$ ist eine Spiegelung des Punktes $E$ an der virtuellen Strecke ${\overline {HO}}$. Somit ist der konstruierte Winkel $\angle {BOE'}$ exakt ein Drittel des gegebenen Winkels $\angle {BOC}$.

• 
  Bild 1
  Tomahawk, die Dreiecke gleicher Größe sind in Rot/Gelb/Grün hervor gehoben
• 
  Bild 2
  Schablone (schematische Darstellung) zur Dreiteilung von Winkeln von 90° (rot) bis 180° (blau)
    
• 
  Bild 3
  Gleichschenkliges Dreieck $\triangle EOE^{\prime }$ mit Höhe $|OH|={\tfrac {r}{2}}$
• 
  Bild 4
  Position des Tomahawks (hellblau) für kleine Winkel

Teilung mit einem rechtwinkligen dreieckigen Lineal

Dreiteilung des Winkels mittels des Rechtwinkelhakens nach Ludwig Bieberbach, Animation, am Ende 60 s Pause

Im Jahr 1932 veröffentlichte Ludwig Bieberbach seine Arbeit Zur Lehre von den kubischen Konstruktionen. Er führt darin aus:

„Im folgenden soll gezeigt werden, daß man alle kubischen Konstruktionen lösen kann, wenn man neben üblichem Gebrauch von Zirkel und Lineal noch folgende Verwendung des Rechtwinkelhakens gestattet: Er ist so hinzulegen, daß sein einer Schenkel durch einen gegebenen Punkt geht, daß sein anderer Schenkel einen gegebenen Kreis berührt, sein Scheitel aber auf einer gegebenen Gerade liegt, wo er den neu zu konstruierenden Punkt markiert.“

– Ludwig Bieberbach: Journal für die reine und angewandte Mathematik, DigiZeitschriften

Der Winkel $\delta$ soll gedrittelt werden. Setzt man

$\alpha =\cos(\delta )$  und  $z=\cos \left({\frac {\delta }{3}}\right),$

führt dies zur Gleichung

$z^{3}-{\frac {3}{4}}z-{\frac {\alpha }{4}}=0.$

Die folgende Beschreibung der nebenstehenden animierten Konstruktion – angelehnt an die von Bieberbach – enthält deren Weiterführung bis zur vollständigen Dreiteilung des Winkels.

Es beginnt mit dem ersten Einheitskreis (Basis für Bieberbachs Beweisführung, prinzipiell ist auch ein Kreis mit beliebigem Radius zielführend) um seinen Mittelpunkt $A$, dem ersten Winkelschenkel ${\overline {BP}}$ und dem daran anschließenden zweiten Einheitskreis um $P$. Nun wird der Durchmesser ${\overline {BP}}$ ab $P$ bis zur Kreislinie des zweiten Einheitskreises verlängert, dabei ergibt sich der Schnittpunkt $O$. Es folgen der Kreisbogen um $P$ mit dem Radius ${\overline {PB}}$ und das Einzeichnen des zweiten Winkelschenkels des zu drittelnden Winkels $\delta$, dabei ergibt sich der Punkt $C$.

Jetzt kommt das so genannte zusätzliche Konstruktionsmittel zum Einsatz, im dargestellten Beispiel ist es das Geodreieck. Dieses legt man jetzt auf folgende Art und Weise auf die Zeichnung: Der Scheitel des Winkels $90^{\circ }$ bestimmt auf dem Winkelschenkel ${\overline {PC}}$ den Punkt $S$, eine Kathete des Dreiecks verläuft durch den Punkt $O$ und die andere tangiert den Einheitskreis um $A$. Nach dem Verbinden des Punktes $O$ mit $S$ und dem Einzeichnen der Tangente ab $S$ an den Einheitskreis um $A$ zeigt sich der oben genannte Rechtwinkelhaken. Der von den Strecken ${\overline {OS}}$ und ${\overline {PS}}$ eingeschlossene Winkel ist somit exakt ${\tfrac {\delta }{3}}$. Es geht weiter mit der Parallelen zu ${\overline {OS}}$ ab $P$, dabei ergeben sich der Wechselwinkel oder Z-Winkel ${\tfrac {\delta }{3}}$ und der Punkt $D$ auf dem Kreisbogen um $P$. Eine weitere Parallele zu ${\overline {OS}}$ ab $A$ bestimmt den Berührungspunkt $E$ der Tangente an den Einheitskreis um $A$. Abschließend noch eine gerade Linie von $P$ durch $E$ ziehen, bis sie den Kreisbogen um $P$ in $F$ schneidet.

Somit ist der Winkel $\delta$ wegen ${\overline {PS}}=2\cdot \cos \left({\tfrac {\delta }{3}}\right)$ exakt gedrittelt.

Kurven

→ Hauptartikel: Trisektrix

Als Trisektrix bezeichnet man eine Kurve, die das exakte Dritteln eines Winkels mit Zirkel und Lineal ermöglicht. Die Existenz beziehungsweise Konstruierbarkeit der Kurve mit anderen Mitteln als Zirkel und Lineal ist hierbei gegeben und unter Zuhilfenahme dieser Kurve als einziges zusätzliches Hilfsmittel ist es dann möglich, einen Winkel zu dritteln. Im Gegensatz zur reinen Konstruktion mit Zirkel und Lineal können Punkte so nicht nur durch den Schnitt von Geraden und Kreisen konstruiert werden, sondern auch durch den Schnitt von Geraden und Kreisen mit der gegebenen Kurve. Die Gesamtheit der Kurvenpunkte selbst ist dabei aber nicht mit Zirkel und Lineal konstruierbar, weshalb die Verwendung einer solchen Kurve eine Verletzung der klassischen Regeln zur Winkeldreiteilung darstellt.

Dreiteilung unterschiedlicher Winkel mithilfe der Sinuskurve

Dreiteilung des Winkels mittels der Sinuskurve

→ Hauptartikel: Sinus und Kosinus

Hung Tao Sheng veröffentlichte im Jahr 1969 im Mathematics Magazine den Artikel A Method of Trisection of an Angle and X-Section of an Angle. Darin beschreibt u. a. eine Methode die zur Dreiteilung eines beliebigen Winkels die Sinuskurve verwendet.

Vorgehensweise

Es beginnt mit dem Viertelkreis um $A$ mit Radius gleich $1\;[LE]$ und der Verlängerung der Strecke ${\overline {AB}}$ über $B$ hinaus. Beim Eintragen der Sinuskurve mittels Schablone oder einer sogenannten Dynamische-Geometrie-Software (DGS) ergibt sich auf der Verlängerung die Kreiszahl $\pi$ als Schnittpunkt. Der zu drittelnde Winkel $3\alpha$ wird mit den Winkelschenkeln ${\overline {AB}}$ und ${\overline {AD}}$ bestimmt.

Es folgt eine Parallele zu ${\overline {AB}}$ ab $D$ bis sie die Sinuskurve im 2. Quadranten im Punkt $D_{1}$ schneidet. Das anschließend gefällte Lot ab $D_{1}$ hat den Fußpunkt $D_{2}$. Die darauffolgende Dreiteilung des Abstandes $|D_{2}\pi |$ erzeugt, unter Verwendung des ersten Strahlensatzes, die Teilungspunkte $E$ und $F$. Die Übertragung dieser Punkte auf die Sinuskurve ergeben die Schnittpunkte $E_{1}$ und $F_{1}$. Schließlich liefern die zwei Parallelen zu ${\overline {DD_{1}}}$ ab $E_{1}$ und $F_{1}$ mit den Schnittpunkten $E_{2}$ und $F_{2}$ die Dreiteilung des gegebenen Winkels $3\alpha$.

Dreiteilung unterschiedlicher Winkel mithilfe einer einzigen Hyperbel

Dreiteilung des Winkels mithilfe einer einzigen Hyperbel
Hyperbelgleichung $y^{2}=3x^{2}-2sx,$
die Kreissehne ${\overline {S_{2}F_{1}}}$ (grün) ist konstant

→ Hauptartikel: Hyperbel, Hyperbel als Trisektrix

Im Jahr 1902 veröffentlichte K. Matter den Aufsatz Zur Trisektion des Winkels. Darin zeigt er eine Methode, die es ermöglicht, mit nur einer Hyperbel unterschiedliche Winkel zu dritteln.

„Eine von der […] allgemeinen Methode etwas abweichende, hübsche und einfache geometrische Lösung unseres Problems der Dreiteilung des Winkels ist die folgende, bei welcher die Konstruktion einer einzigen Hyperbel in Verbindung mit einem Kreis nötig wird.“

– K. Matter: Zur Trisektion des Winkels

Auswahl der bekanntesten Trisektrizes

• Trisektrix des Hippias (5. Jahrhundert v. Chr.) sowie die
• Spirale des Archimedes (3. Jahrhundert v. Chr.) gehören zu den ältesten Beispielen für solche Kurven.
• Hyperbel als Trisektrix, diese Kurve nutzte Pappos im 4. Jahrhundert n. Chr. zur Lösung dieses Problems.
• Parabel als Trisektrix, beschrieben von René Descartes in seinem Werk La Geometria aus dem Jahr 1637.
• Pascalschnecke als Trisektrix, gefunden vom französischen Juristen Étienne Pascal um das Jahr 1637.
• Zykloide von Ceva, entdeckt vom italienischen Jesuiten Tommaso Ceva (1648–1736), ermöglicht ebenfalls, einen beliebigen Winkel zu dritteln.
• Maclaurin-Trisektrix, wurde von Colin Maclaurin im Jahr 1742 untersucht.
• Trisektrix von Longchamps, stammt vom französischen Mathematiker Gohierre de Longchamps (1842–1906).

Dreiteilung des Winkels mit Origami

Während die Dreiteilung des Winkels mit den klassischen Instrumenten der Geometrie nicht möglich ist, kann die Aufgabe mit der Papierfalttechnik Origami – so wie die Würfelverdoppelung – gelöst werden. Verwendet wird hierfür ein rechteckiges oder quadratisches Blatt Papier. Für die Dreiteilung eines Winkels $0^{\circ }<3\alpha <90^{\circ }$ bedarf es sechs Faltungen des Blattes.

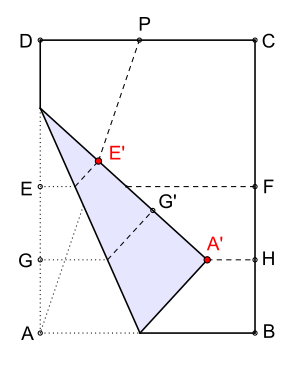
Zuerst wird das Blatt in der Mitte gefaltet (siehe Bild 1), dabei ergeben sich an den beiden Blattkanten die Punkte $E$ und $F.$ Alternativ kann ${\overline {EF}}$ auch mit einer frei wählbaren Länge der Strecke ${\overline {AE}}$ festgelegt werden. Es folgt die Falte ${\overline {GH}},$ sie halbiert die Strecke ${\overline {AE}}.$ Punkt $P$ wird nun nach Belieben (siehe Bild 2) auf der Strecke ${\overline {CD}}$ bestimmt und im Anschluss das Blatt von $A$ bis $P$ gefaltet. Damit ergibt sich der Winkel $3\alpha$ am Scheitel $A.$

Jetzt folgt die maßgebende vierte Faltung (siehe Bild 3) zur Dreiteilung des Winkels $3\alpha$, indem man zuerst die Ecke $A$ auf die Falte ${\overline {GH}}$ und den Punkt $E$ auf die Falte ${\overline {AP}}$ legt. Nach dem Markieren des Punktes $A'$ auf das Blatt, wird die Ecke $A$ zurückgebogen und der Schnittpunkt $I$ markiert – entstanden durch die vierte Falte mit ${\overline {GH}}$ – das Blatt hat so wieder seine rechteckige Form.

Abschließend (siehe Bild 4) noch die Falte von $A$ durch $I$ sowie die von $A$ durch $A'$ knicken. Die Faltlinien ${\overline {AG'}}$ und ${\overline {AA'}}$ teilen den Winkel $3\alpha$ in drei (exakt) gleiche Teile.

• 
  Bild 1
  Falten der ersten beiden Faltlinien, ${\overline {EF}}$ muss nicht die Mitte des Blattes sein
• 
  Bild 2
  Die dritte Falte liefert den Winkel $3\alpha$
• 
  Bild 3
  Die entscheidende vierte Falte, Ecke $A$ auf ${\overline {GH}}$ und $E$ auf ${\overline {AP}}$
• 
  Bild 4
  Die Faltlinien ${\overline {AG'}}$ und ${\overline {AA'}}$ teilen den Winkel $3\alpha$ in drei gleiche Teile

Dreiteilung des Winkels mithilfe eines flexiblen Lineals

In dieser Methode wird auf einer zylindrischen Mantelfläche eine Schraubenlinie (Helix) aufgetragen, die von einer dreidimensionalen Linie an vier Stellen geschnitten wird. Die beiden inneren Schnittpunkte dritteln den Winkel, der durch die beiden äußeren vorgegeben ist. Bei genauer Betrachtung sieht man die Ähnlichkeit der Konstruktion mit der Methode Quadratrix des Hippias. Anstatt der euklidischen Werkzeuge – Zirkel und Lineal – werden hierfür ein zylindrischer Körper mit gegebenem Kreismittelpunkt $M$ des Zylinders, ein flexibles Lineal (z. B. Rollbandmaß) und z. B. ein Anschlagwinkel verwendet.

Vorgehensweise

Zuerst wird vom Kreismittelpunkt $M$ der Winkelschenkel ${\overline {MA}}$ eingezeichnet (siehe Bild 1) und der zu drittelnde Winkel $3\alpha$ mittels des Winkelschenkels ${\overline {MB}}$ bestimmt. Es folgt das Einzeichnen der beiden (roten) Strecken ${\overline {AC}}$ und ${\overline {BD}}$ auf die Mantelfläche mithilfe des flexiblen Lineals oder alternativ z. B. mithilfe eines (rechtwinkligen) Anschlagwinkels.

Es geht weiter mit dem Auftragen der Schraubenlinie (grün) auf die zylindrische Mantelfläche (siehe Bild 2). Das flexible Lineal wird an die Zylinderkante gelegt und fixiert. Es folgen fünf Wicklungen mit gleicher Ganghöhe $h,$ sie entspricht der Breite des Lineals. Das Einzeichnen der Schraubenlinie geschieht bei schrittweisem Abwickeln, jeweils an der freien Kante des Lineals. Nun werden die Schnittpunkte $E$ mit der ersten Wicklung der Schraubenlinie und $F$ mit der vierten Wicklung markiert.

Das flexible Lineal wird nun so auf die zylindrische Mantelfläche (siehe Bild 3) gesetzt, dass die Kante des Lineals durch die Punkte $E$ und $F$ verläuft. Nach dem Einzeichnen der Kurvenlinie (hellblau) durch $E$ und $F$ folgt das Markieren der Schnittpunkte $G$ und $I$ auf der Schraubenlinie. In diesem Fall ist diese Linie – ebenfalls eine Schraubenlinie mit einer sehr großen Ganghöhe – die kürzeste Verbindung der beiden Punkte $E$ und $F.$ Abschließend werden mithilfe des flexiblen Lineals, oder alternativ z. B. mithilfe eines Anschlagwinkels, die Strecken ${\overline {IJ}}$ und ${\overline {JM}}$ sowie ${\overline {GH}}$ und ${\overline {HM}}$ eingetragen.

Wegen $|AJ|=|JH|=|HB|$ ist somit der Winkel $3\alpha$ exakt dreigeteilt.

• 
  Bild 1
  Einzeichnen des Winkels $3\alpha$ und der beiden (roten) Strecken ${\overline {AC}}$ und ${\overline {BD}}$ mit dem flexiblen Lineal oder alternativ mithilfe eines (rechtwinkligen) Anschlagwinkels
• 
  Bild 2
  Schraubenlinie (grün) auf die Mantelfläche mithilfe des flexiblen Lineals auftragen
• 
  Bild 3
  Kurvenlinie (hellblau) durch $E$ und $F$ mithilfe des flexiblen Lineals einzeichnen, Schnittpunkte $G$ und $I$ auf die Kreisfläche projizieren

Näherungsverfahren

Albrecht Dürers Näherung der Dreiteilung

Dreiteilung des Winkels, eine Näherungskonstruktion nach Dürer

Karl Hunrath veröffentlichte 1906 eine Untersuchung zu Dürers Näherungslösung der Winkeldreiteilung aus dem Jahr 1525 in der Zeitschrift Heidelberger Texte zur Mathematikgeschichte.

Konstruktionsbeschreibung

In einem gegebenen Kreissektor mit Mittelpunkt $O$ und einem Mittelpunktswinkel $\angle {AOB}$ größer $90^{\circ }$ wird die Sehne ${\overline {AB}}$ in $C$ und $D$ gedrittelt. Es folgt das Errichten der beiden Senkrechten auf ${\overline {AB}}$ in $C$ und $D$, dabei ergeben sich die Schnittpunkte $E$ bzw. $F$ mit dem Kreisbogen. Nun wird ein Kreisbogen mit dem Radius ${\overline {AE}}$ ab $E$ und ein zweiter mit dem Radius ${\overline {BF}}$ ab $F$ gezogen, bis sie die Sehne ${\overline {AB}}$ in $E_{1}$ bzw. in $F_{1}$ schneiden. Nach dem Dritteln der Strecke ${\overline {CE_{1}}}$ nahe dem Punkt $E_{1}$ und der Strecke ${\overline {DF_{1}}}$ nahe dem Punkt $F_{1}$ ergeben sich die Schnittpunkte $G_{1}$ bzw. $H_{1}.$ Die Projektion der Punkte $G_{1}$ und $H_{1}$ auf den Kreisbogen liefert die gesuchten Punkte $G$ und $H.$ Die Verbindungslinien (rot) $G$ mit $O$ sowie $H$ und $O$ teilen den Mittelpunktswinkel $\angle AOB$ in annähernd drei gleiche Teile.

Dieses Ergebnis wird mit zwei Iterationsschritten erreicht. Nach der ersten Iteration ergeben sich die Winkel $\angle {EOA},$ $\angle {FOE}$ und $\angle {BOF}.$

Die eingezeichneten Punkte $K,L(\neq G),M(\neq H),N$ und $Q$ sowie die mittige Strecke ${\overline {OI}}$ werden für die Konstruktion nicht benötigt, sie dienen ausschließlich dem von Hunrath ausführlich erörterten Beweis.

Fehlerbetrachtung

Dürers Näherungslösung zeigt bei Winkeln $0^{\circ }<2\alpha \leq 180^{\circ }$ nur sehr geringe absolute Fehler $F_{a}.$

Dreiteilung des Winkels $2\alpha$ nach Dürer absoluter Fehler $F_{a}$ des Winkels $\beta =\angle GOA=\angle BOH,$ $1''=0{,}0002{\overline {7}}\mathrm {^{\circ }}$
Winkel $2\alpha$	Winkel $2\alpha /3$	Winkel $\beta$	$F_{a}$	$F_{a}$
0$30^{\circ }$	$10^{\circ }$	0$9^{\circ }\;59'\;59{,}992''$	$-0{,}007''$	$-0{,}0000019{\overline {4}}\mathrm {^{\circ }}$
0$45^{\circ }$	$15^{\circ }$	$14^{\circ }\;59'\;59{,}879''$	$-0{,}12''$	$-0{,}0000{\overline {3}}\mathrm {^{\circ }}$
0$60^{\circ }$	$20^{\circ }$	$19^{\circ }\;59'\;59{,}093''$	$-0{,}906''$	$-0{,}000251{\overline {6}}\mathrm {^{\circ }}$
0$90^{\circ }$	$30^{\circ }$	$29^{\circ }\;59'\;44{,}504''$	$-15{,}495''$	$-0{,}0043041{\overline {6}}\mathrm {^{\circ }}$
$120^{\circ }$	$40^{\circ }$	$39^{\circ }\;58'\;4{,}427''$	$-1'\;55{,}572''$	$-0{,}03210{\overline {3}}\mathrm {^{\circ }}$
$150^{\circ }$	$50^{\circ }$	$49^{\circ }\;50'\;56{,}209''$	$-9'\;3{,}79''$	$-0{,}151052{\overline {7}}\mathrm {^{\circ }}$
$180^{\circ }$	$60^{\circ }$	$59^{\circ }\;28'\;22{,}498''$	$-31'\;37{,}501''$	$-0{,}5270836{\overline {1}}\mathrm {^{\circ }}$

Näherung durch iterative Winkelhalbierung

Dieses weniger effiziente, aber viel einfachere Verfahren verwendet die geometrische Reihe

${\frac {\alpha }{3}}=\alpha \cdot \left({\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+{\frac {1}{32}}-{\frac {1}{64}}+\dots \right)$

Beispiel Winkel $60^{\circ }$ nach neun Iterationen

$60^{\circ }\cdot \left({\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+{\frac {1}{32}}-{\frac {1}{64}}+{\frac {1}{128}}-{\frac {1}{256}}+{\frac {1}{512}}\right)=60^{\circ }\cdot {\frac {171}{512}}=20{,}0390625^{\circ }$

Es ist zu beachten, dass die folgende Formel gilt:

$\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{2^{k}}}={\frac {1}{3}}-{\frac {(-1)^{n}}{3\cdot 2^{n}}}.$

Es gibt damit auch einen indirekten Zusammenhang mit der Darstellung ${\frac {1}{3}}=[0{,}010101\dots ]_{2}=[0{,}{\overline {01}}]_{2}$ im Binärsystem.

Näherung für Winkelweiten größer 0° bis 90°

Im Jahr 2011 sandte Chris Alberts eine außerordentlich gute Näherung einer Winkeldreiteilung an Rouben Rostamian (University of Maryland, Baltimore County).

Rostamian hat die Konstruktion von Alberts umformuliert und neu geordnet, aber die Unterschiede zum Original sind, so sagt er, nur kosmetisch. Zu Beginn der Konstruktionsbeschreibung verweist er auf eine Erläuterung („Explanation here“), in der er auch die Gründe aufzeigt, weshalb von dieser Konstruktion keine Bilder zu sehen sind. Nichtsdestotrotz ist die im Folgenden dargestellte Konstruktion allein mithilfe Rostamians Beschreibung machbar.

Näherungskonstruktion für Winkel größer 0° bis 90° nach Chris Alberts

Animation mit Schrittgrößen ca. 3°, aus Gründen der Übersichtlichkeit sind die Punkte ohne Beschriftung

Konstruktion

(Übersetzung)

Betrachte den Kreisbogen $AB$ auf dem Kreis $C$, der in $O$ zentriert ist (siehe Bild). Angenommen, der Winkel $\angle {AOB}$ liegt zwischen $0$ und $90$ Grad, dann gehe folgendermaßen vor, um $\angle {AOB}$ zu teilen:

1. Zeichne den Kreis ${C'}$ um $O$ mit einem Radius ${\tfrac {1}{3}}{\overline {OA}};$ die Schnittpunkte mit den Strecken ${\overline {OA}}$ bzw. ${\overline {OB}}$ sind ${A'}$ bzw. ${B'}.$
2. Ziehe den Kreis ${C''}$ (grün dargestellt) um ${B'}$ durch den Punkt $O.$
3. Es sei $E$ der Mittelpunkt der Strecke ${\overline {OB'}}.$ Zeichne eine Linie ab $E$ parallel zu ${\overline {OA}}$ durch die Kreislinie von ${C''}$ bis zum Kreis ${C'};$ die Schnittpunkte sind $P$ bzw. $R.$
4. Es sei $M$ der Mittelpunkt der Strecke ${\overline {PR}}.$ Ziehe eine Linie ab ${B'}$ durch $M,$ bis sie den Kreis ${C'}$ in $N$ schneidet.
5. Zeichne eine Linie ab ${B'}$ parallel zu ${\overline {OA}}$ und wähle den Punkt $F$ darauf so, dass ${\overline {NB'}}={\overline {NF}}$ ist.
6. Verlängere die Strecke ${\overline {NF}},$ bis sie den Kreis $C$ in $G$ schneidet.
7. Ziehe die Linie ab $G$ durch $O$ bis sie den Kreis ${C'}$ in ${H}$ schneidet.

Hinweis: Sieht man sich die Zeichnung genau an, ist zu erkennen, dass sich die Strecken ${\overline {GO}}$ und ${\overline {GN}}$ nicht überdecken, d. h. nicht kollinear sind.

8. Es sei $D$ diametral gegenüber dem Punkt ${B'}$ im Kreis ${C'}.$ Ziehe eine Linie ab $D$ parallel zu ${\overline {OA}}$ und wähle den Punkt $J$ darauf so, dass der Abstand $|HD|={\overline {HJ}}$ ist.

Hinweis: Die Strecke ${\overline {HJ}}$ ist keine Verlängerung der Strecke ${\overline {GH}}.$

9. Verlängere die Strecke ${\overline {HJ}},$ bis sie den Kreis $C$ in $K$ schneidet.
10. Spiegle $K$ an der Strecke ${\overline {OA}},$ um den Punkt $T$ zu erhalten.

Der Winkel $\angle {AOT}$ ist nahezu gleich einem Drittel des Winkels $\angle {AOB}.$

Fehleranalyse

Rostamian führte eine Fehleranalyse durch, u. a. mit folgenden Ergebnissen: Die obigen Konstruktionsschritte (1.–10.) beinhalten drei Stufen der Näherungsgrade, d. h. drei unterschiedliche Fehlergrößen im Bereich zwischen $0^{\circ }$ und $90^{\circ }$:

• Stufe 1: Nach dem 5. Schritt ist die Differenz des Winkels $\angle {F{B'}N}$ zu einem exakt gedrittelten Winkel max. $0{,}7^{\circ }.$
• Stufe 2: Nach dem 7. Schritt ist die Differenz des Winkels $\angle {{A'}OH}$ zu einem exakt gedrittelten Winkel nur noch max. $0{,}00013791^{\circ }.$
• Stufe 3: Nach dem 10. Schritt hat der Winkel $\angle {AOT}$ zu einem exakt gedrittelten Winkel den hervorragenden kleinen Differenzwert von max. $\left(1{,}33\cdot 10^{-16}\right)^{\circ }.$

Die dargestellte Konstruktion wurde mit der Dynamische-Geometrie-Software (DGS) GeoGebra angefertigt; darin werden in diesem Fall die Winkelgrade mit signifikanten dreizehn Nachkommastellen angezeigt. Die sehr kleinen Fehler des Winkels $\angle {AOT},$ sprich, die Differenzen ${\tfrac {\alpha }{3}}-\beta ,$ werden deshalb von GeoGebra stets mit $0^{\circ }$ angezeigt.

Verdeutlichung des absoluten Fehlers

Zwischen den Winkeln $0^{\circ }$ und $90^{\circ }$ ist nahe $70^{\circ }$, mit einem Differenzwert max. $\left(1{,}33\cdot 10^{-16}\right)^{\circ }$, der Fehler am größten. Dies entspricht einem absoluten Fehler $F_{a}$ der – nicht eingezeichneten – Sehne ${\overline {AT}}$:

$F_{a}=2\cdot \sin \left({\frac {\left(1{,}33\cdot 10^{-16}\right)^{\circ }}{2}}\right)=0{,}00000000000000000232\ldots =2{,}32\ldots \cdot 10^{-18}\;[\mathrm {LE} ]$

Anschaulich: Hätten die Winkelschenkel die Länge gleich 1 Billion km (das Licht bräuchte für diese Strecke fast 39 Tage), wäre der absolute Fehler der Sehne ${\overline {AT}}$ ca. 2,32 mm.

Anwendungen

Lösung kubischer Gleichungen

Eine kubische Gleichung mit reellen Koeffizienten kann genau dann geometrisch mit Zirkel, Lineal und einem Winkeldreiteiler gelöst (d. h. deren Lösungen konstruiert) werden, wenn sie drei reelle Lösungen hat. Dabei werden die Koeffizienten des Polynoms als gegeben gesehen und bei der Konstruktion verwendet. Insbesondere kann die Kubikwurzel aus 2, die bei der Verdopplung des Würfels benötigt wird, nicht über diese Werkzeuge konstruiert werden, da die Gleichung $x^{3}-2=0$ nicht ausschließlich reelle Lösungen besitzt.

Ein regelmäßiges Vieleck mit $n$ Seiten lässt sich genau dann mit Lineal, Zirkel und Winkeldreiteiler konstruieren, wenn $n=2^{r}3^{s}p_{1}\cdots p_{k}$ mit paarweise verschiedenen Fermatschen Primzahlen $p_{j}$ größer als 3 der Form $p_{j}=2^{t}3^{u}+1$, vgl. dazu auch Pierpont-Primzahl.

Mithilfe der kubischen Gleichung des Siebenecks wird im Folgenden exemplarisch erläutert, wie damit der Kosinus des Winkels gefunden wird, der mithilfe eines sogenannten zusätzlichen Hilfsmittels (z. B. Tomahawk) gedrittelt werden kann.

Das Siebeneck hat die kubische Gleichung

$(1)\;\;X^{3}+X^{2}-2X-1=0.$

Setzt man $X={\tfrac {\left(Y-1\right)}{3}},$ ergibt sich $1+6\cdot \cos({\tfrac {2\pi }{7}})$ $(=1+3\eta )$ als eine Lösung von

$(2)\;\;Y^{3}-21Y-7=0.$

Durch Einsetzen von

$Y={\sqrt {28}}\cdot \cos(\theta )$

vereinfacht es sich zu

$7\cdot {\sqrt {28}}\left(4\cdot \cos ^{3}(\theta )-3\cdot \cos(\theta )\right)=7;$

schließlich erhält man den Kosinus des Winkels, der gedrittelt werden kann:

$\cos(3\theta )={\frac {1}{\sqrt {28}}}$.

Im Folgenden wird am Beispiel Siebeneck beschrieben, wie die kubische Gleichung

$(1)\;\;X^{3}+X^{2}-2X-1=0$

ermittelt wird. Es beginnt mit dem Zeichnen eines regelmäßigen Siebenecks.

Konstruktionsbeschreibung

Siebeneck nach Andrew M. Gleason, Konstruktionsskizze für die Ermittlung des Winkels $3\theta ,$ der mit einem zusätzlichen Hilfsmittel gedrittelt werden kann.

1. Umkreis des Siebenecks mit dem Radius $r=6$ um den Nullpunkt $O$ eines kartesischen Koordinatensystems.
2. Markieren der Punkte $A(6|0),P(-1|0),Q(-3|0)$ und $R(3|0).$
3. Ein Kreisbogen mit Radius ${\overline {RQ}}$ schneidet die $y$-Achse in $K(0|{\sqrt {27}})$ und $L(0|-{\sqrt {27}});$ die Strecke ${\overline {KL}}$ ist die Seite eines gleichseitigen Dreiecks mit Umkreisradius ${\overline {RQ}}.$
4. Verbindung der Punkte $P$ mit $K$ und $P$ mit $L;$ der Winkel $\angle {APK}$ entspricht $3\theta .$
5. Bogen um $P$ mit Radius ${\overline {PK}}.$
6. Dreiteilung des Winkels $3\theta ,$ z. B. mithilfe eines Tomahawks, ergibt den Schnittpunkt $S.$
7. Parallele zu ${\overline {KL}}$ durch $S$ ergibt die Schnittpunkte $B,T$ und $G;$ $B$ und $G$ sind Eckpunkte des – nicht eingezeichneten – regelmäßigen Siebenecks $ABCDEFG.$

Nachweis der Konstruktion

Sei $U$ der Schnittpunkt der Strecke ${\overline {ST}}$ mit der $x$-Achse. Aus der Konstruktion geht hervor, dass

${\overline {PK}}={\sqrt {28}},\;\;\cos \left(\angle {APK}\right)={\frac {1}{\sqrt {28}}},\;\;{\overline {PU}}={\sqrt {28}}\cdot \cos \left(\angle {APS}\right)={\sqrt {28}}\cdot \cos \left({\frac {1}{3}}\angle {APK}\right).$

Die Konstruktion ist korrekt, wenn

${\overline {OU}}=6\cdot \cos \left({\frac {2\pi }{7}}\right);$  oder gleichwertig, wenn  ${\overline {PU}}=1+6\cdot \cos \left({\frac {2\pi }{7}}\right),$

wobei die Normierung des Kosinus um den Faktor $6$ von der Wahl des Radius $r=6$ herrührt. Man muss also nur folgende Identität feststellen:

${\sqrt {28}}\cdot \cos \left({\frac {1}{3}}\arccos \left({\frac {1}{\sqrt {28}}}\right)\right)=1+6\cdot \cos \left({\frac {2\pi }{7}}\right).$

Um dies zu tun, sei

$\xi =\cos \left({\frac {2\pi }{7}}\right)+i\cdot \sin \left({\frac {2\pi }{7}}\right)$

eine primitive siebte Einheitswurzel in $\mathbb {C}$. Setze

$\eta =\xi +\xi ^{-1}=2\cdot \cos \left({\frac {2\pi }{7}}\right),$

dann ist

$\eta ^{3}+\eta ^{2}-2\eta -1=\xi ^{3}+\xi ^{2}+\xi +1+\xi ^{-1}+\xi ^{-2}+\xi ^{-3}=0.$

Somit ist $\eta$ eine Wurzel der kubischen Gleichung

$(1)\;\;X^{3}+X^{2}-2X-1=0.$

Wie oben beschrieben, erhält man daraus den Kosinus des Winkels $3\theta$:

$\cos(3\theta )={\frac {1}{\sqrt {28}}}.$

Dreiteilung des Zentriwinkels eines regelmäßigen Polygons

Bei regelmäßigen Polygonen mit der Definition $N=6K\pm 1$ ($K$ für eine ganze positive Zahl) ist eine Dreiteilung des Zentriwinkels ${\tfrac {2\pi }{N}}$ ($N$ für Eckenanzahl) möglich. Erreicht wird dies – wie im Folgenden exemplarisch anhand des Siebzehnecks erläutert – indem man ein gleichseitiges Dreieck so um das Polygon legt, dass zwei Ecken und eine Seite des Polygons das Dreieck berühren.

Die Konstruktion des Polygons wird als gegeben betrachtet, unabhängig davon mit welchen zusätzlichen Hilfsmitteln es eventuell erstellt wurde. Von da an ist nur noch eine Konstruktion mit Zirkel und Lineal erlaubt, um das gleichseitige Dreieck zu konstruieren.

Beispiel Zentriwinkel des Siebzehnecks

• Gegeben sei die Konstruktion eines regelmäßigen Siebzehnecks ($N=6\cdot 3-1$) und dessen Mittelpunkt $O$.

Es beginnt mit dem Einzeichnen des Zentriwinkels $\mu =3\alpha ={\tfrac {2\pi }{17}}$ und Benennen der Eckpunkte des Siebenecks $A,B$ und $C$ diametral gegenüber. Ausgehend vom Eckpunkt $C$ werden mit einem Abstand von jeweils drei Eckpunkten die betreffenden Ecken mit $E$ bzw. $D$ bezeichnet. Nach der Verbindung $E$ mit $D$ zieht man ab dem Mittelpunkt $O$ eine Halbgerade durch $C$, Schnittpunkt $F$ halbiert ${\overline {ED}}$. Es folgt ein Kreisbogen um $D$ mit Radius ${\overline {DF}}$ und ein zweiter mit gleichem Radius um $F$; dabei ergibt sich der Schnittpunkt $G$. Die darauffolgende Sekante des Umkreises durch $D$ und $G$ schneidet in $H$ die Halberade von $O$ durch $C$. Dadurch ergibt sich der Winkel $HDF=60^{\circ }$. Eine zweite Sekante durch die Punkte $H$ und $E$ sowie eine weitere durch $A$ und $B$ generieren das gleichseitige Dreieck $HIJ$. Die beiden Verbindungen $H$ mit $A$ und $H$ mit $B$ schließen am Scheitel $H$ den gesuchten Winkel $\alpha ={\tfrac {2\pi }{51}}$ ein.

• 
  Dreiteilung des Zentriwinkels eines Siebzehnecks mithilfe eines gleichseitigen Dreiecks, dessen Seiten Sekanten des Umkreises sind
• 
  Beweisskizze zur Dreiteilung des Zentriwinkels eines regelmäßigen Polygons

Beweis

Ein möglicher Beweis für Polygone mit der Definition $N=6K\pm 1$ ist, wenn nachgewiesen kann, dass ein derart konstruiertes gleichseitiges Dreieck am Scheitel $H$ den gedrittelten Winkel $\alpha ={\tfrac {2\pi }{51}}$ erzeugt. Die folgende Beweisführung benötigt zu Beginn den Zentriwinkel sowie dessen gedrittelten Winkel eines beliebigen regelmäßiges Polygons das $N=6K\pm 1$ erfüllt. Hierzu ist es vorteilhaft, wenn die benötigten Winkelweiten einfach zu konstruieren sind, wie dies beim kleinstmöglichen Polygon, dem regelmäßigen Fünfeck ($N=6\cdot 1-1$) mit dem Zentriwinkel $3\alpha =72^{\circ }$ und dem gedrittelten Winkel $\alpha =24^{\circ }$ zutrifft.

Vorgehensweise

Zuerst wird der Umkreis mit beliebigem Radius um den Mittelpunkt $O$ gezogen und die Mittelachse ab der Kreislinie durch $O$ eingezeichnet. Der Zentriwinkel $3\alpha$ ($\angle {AOB}$) und dessen gedrittelter Winkel $\alpha$ ($\angle {COD}$) eines Fünfecks werden so eingetragen, dass die Mittelachse sie halbiert. Zieht man nun eine Halbgerade von $A$ durch $D$ bis sie die Mittelachse in $H$ schneidet, sieht es so aus, als sei $3\alpha$ nach der Methode des Archimedes geteilt worden.

Nach dem Verbinden des Punktes $C$ mit $D$, ergibt Schnittpunkt $E$, dreht man den Winkel $\alpha$ um $60^{\circ }$ gegen den Uhrzeigersinn und erhält somit den Winkel $C'OD'$. Da das rechtwinklige Dreieck $C'OE'$ kongruent ist mit dem rechtwinkligen Dreieck $COE$, schneidet eine Sekante des Umkreises durch $D',E'$ und $C'$ die Mittelachse im Schnittpunkt $H'$ gleich $H$.

Sprich das rechtwinklige Dreieck $OH'E'$ mit dem Winkel $30^{\circ }$ am Scheitel $H'$ gleich $H$ ist der sechste Teil eines gleichseitigen Dreiecks, das am Scheitel $H$ den gedrittelten Winkel $\alpha$ liefert.

Was zu beweisen war.

Satz von Morley

Satz von Morley, Konstruktionsskizze

Auch wenn es im ersten Moment den Anschein hat, der Satz von Morley wäre für die Dreiteilung eines beliebigen Winkels geeignet, dem ist nicht so.

In einem vorgegebenen Dreieck $ABC$ werden zuerst die Winkel an den Scheitelpunkten $A,B$ und $C$ gedrittelt. Dazu bedarf es eines zusätzlichen Hilfsmittels, z. B. einer Dynamische-Geometrie-Software (DGS). Die damit exakt erzeugten Winkeldreiteilenden (rot) liefern die Eckpunkte $D$, $E$ und $F$ des Morley-Dreiecks.

Satz von Morley:

„Die drei Schnittpunkte der drei anliegenden Winkeldreiteilenden eines beliebigen Dreiecks bilden ein gleichseitiges Dreieck.“

– Horst Hischer: Das Morley-Dreieck zwischen Anwendung und Spiel

Literatur

• Ernst-Erich Doberkat: Die Dreiteilung des Winkels. In: Die Drei (S. 59–85), Springer Verlag, 2019.
• Underwood Dudley: The Trisectors. Mathematical Association of America, 1996.
• Underwood Dudley: A budget of trisections. Springer Verlag, 1987.
• Christoph Scriba, Peter Schreiber: 5000 Jahre Geometrie. Springer Verlag, 2010.

Weblinks

Wikiversity: Ein Unmöglichkeitsbeweis für die Winkeldreiteilung – Kursmaterialien

Commons: Dreiteilung des Winkels – Sammlung von Bildern

• Eric W. Weisstein: Angle Trisection. In: MathWorld (englisch).
• Jim Loy: Trisection of an Angle (Memento vom 1. Januar 2014 im Internet Archive)
• Matroids Matheplanet: Winkeldreiteilung und der Satz von Haga.
• Schweizer Fernsehen: Origami löst unlösbare Probleme. Einstein, 9. April 2009.
• Sarah Kuchar: Die Dreiteilung des Winkles – eine Zeitreise. 10. Januar 2016.