Einheitswurzel (Zeitreihenanalyse)
Von einer Einheitswurzel spricht man in der Ökonometrie, speziell in der Zeitreihenanalyse, wenn 1 eine Nullstelle des charakteristischen Polynoms ist. Ein stochastischer Prozess, der eine solche Einheitswurzel besitzt, ist nichtstationär, man spricht auch von einem stochastischen Trend. Das ist insbesondere deswegen wichtig, weil viele statistische Schätzverfahren, wie beispielsweise die Methode der kleinsten Quadrate, stationäre Daten voraussetzen und falsche Ergebnisse liefern, wenn die zugrunde liegenden Reihen nicht stationär sind, wie zum Beispiel im Fall der spurious regression.
Beispiel AR(p)-Prozess[Bearbeiten | Quelltext bearbeiten]
Man betrachte als Beispiel einen zeitdiskreten stochastischen Prozess {}. Man nehme zusätzlich an, dass sich dieser Prozess als autoregressiver Prozess der Ordnung p darstellen lässt :
In dem Fall ist {} ein nicht autokorrelierter stochastischer Prozess mit dem Mittelwert Null und der konstanten Varianz . Der Einfachheit halber nehme man an, dass . Wenn eine Nullstelle des charakteristischen Polynoms
ist, dann hat der stochastische Prozess eine Einheitswurzel oder, anders ausgedrückt, er ist integriert mit Ordnung 1, geschrieben . Wenn eine mehrfache Nullstelle der Ordnung ist, dann ist der stochastische Prozess integriert mit Integrationsordnung .
Beispiel AR(1)-Prozess[Bearbeiten | Quelltext bearbeiten]
Ein spezifischeres Beispiel ist das autoregressive Modell erster Ordnung : . Dieses hat eine Einheitswurzel, wenn . In diesem Fall ist das charakteristische Polynom . Die Lösung der Gleichung ist . Wenn der Prozess eine Einheitswurzel hat, dann ist die Zeitreihe nichtstationär. Das bedeutet die Momente des stochastischen Prozesses hängen von ab. Das ergibt sich wie folgt. In dem Falle einer Einheitswurzel ist der Prozess also
sodass mehrfaches Substituieren ergibt. Folglich ist die Varianz von
Weil aber , hängt die Varianz von ab.
Differenziert man eine mit -ter Ordnung integrierte Zeitreihe mal, erhält man einen stationären Prozess. Gegebenenfalls kann Kointegration vorliegen.
Wahrnehmung von Prozessen mit Einheitswurzel[Bearbeiten | Quelltext bearbeiten]
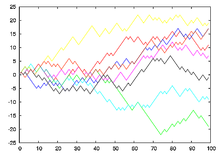
William Feller gibt Wahrscheinlichkeiten dafür an, welche Zeitanteile ein Random Walk, der in Null startet, in den positiven oder in den negativen Zahlen verbringt und weist anhand dieses Beispiels auf eine mögliche Fehleinschätzung hin. Die Wahrscheinlichkeit, dass überwiegend positive oder überwiegend negative Zahlen angenommen werden, ist deutlich größer als die Wahrscheinlichkeit für ein ausgewogenes Verhältnis: Wird beispielsweise beim zwanzigfach wiederholten Wurf einer Münze die Anzahl der Wappen und die Anzahl der Zahlen notiert, ist die Wahrscheinlichkeit, dass im Zeitverlauf entweder Wappen oder Zahl mindestens 16 Mal in Führung liegt, etwa 68,5 %. Dagegen ist die Wahrscheinlichkeit, dass am Schluss Wappen und Zahl gleich oft in Führung gelegen haben, lediglich etwa 6 %. Die intuitive Annahme, dass eine Verdopplung des betrachteten Zeitintervalls eine Verdopplung der Durchgänge durch Null mit sich bringt, ist falsch.[1]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ William Feller: An introduction to probability theory and its applications, zweite Ausgabe, Wiley, 1968, ISBN 0471257087, S. 68. Hans Pécseli: Fluctuations in physical systems, Cambridge University Press, Cambridge 2000, ISBN 0521651921, S. 87.


![{\displaystyle y_{t}=\varepsilon _{t}+\sum _{j\in [1,p]}a_{j}y_{t-j}=a_{1}y_{t-1}+a_{2}y_{t-2}+\cdots +a_{p}y_{t-p}+\varepsilon _{t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c9c5a4d524c1c3e101f5c50df71e005fe639d07)




















