Fehlerfortpflanzung

Dieser Artikel wurde aufgrund von Mängeln auf der Qualitätssicherung Naturwissenschaften eingetragen. Dies geschieht, um die Qualität der Artikel aus den übergreifenden Themengebieten der Naturwissenschaften auf ein akzeptables Niveau zu bringen. Dabei können Artikel gelöscht werden, die nicht signifikant verbessert werden können. Hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.

Bei vielen Messaufgaben ist eine Größe nicht direkt messbar, sondern sie ist indirekt aus mehreren messbaren Größen nach einer festgelegten mathematischen Beziehung zu bestimmen. Da jeder Messwert der einzelnen Größen von seinem richtigen Wert abweicht (siehe Messabweichung, älterer Begriff Messfehler), wird auch das Ergebnis der Rechnung von seinem richtigen Wert abweichen. Die Einzelfehler werden mit der Formel übertragen. Man nennt dieses Fehlerfortpflanzung. Für die Fehlerfortpflanzung existieren Rechenregeln, mit denen die Abweichung des Ergebnisses bestimmt oder abgeschätzt werden kann.

Aufgabe

• Häufig will man ein Ergebnis $y$ aus einer Größe $x$ oder im allgemeinen Fall aus mehreren Größen $x_1$ , $x_2$ , $\cdots$  berechnen. Mit fehlerbehafteter Bestimmung der Eingangsgröße(n) wird auch die Ergebnisgröße falsch berechnet. Nach groben Fehlern muss man neu rechnen. Sonst ist es eher angebracht, nur die Auswirkung des Fehlers bzw. der Fehler auf das Ergebnis zu bestimmen.
• Mathematisch gesagt: Hat man eine Funktion $y= y(x_1 \,,\ x_2 \,,\ \cdots\ )$ mit mehreren unabhängigen Variablen $x_i$ , die um ein kleines $\Delta x_i$ falsch sind, so wird auch das Ergebnis $y$ falsch um ein kleines $\Delta y$. Dieses $\Delta y$ sollte man berechnen können.
• Messtechnisch gesagt: Hat man ein Messergebnis aus Messwerten verschiedener Größen auszurechnen, wobei diese Messwerte von ihren richtigen Werten abweichen, so wird man ein Ergebnis berechnen, das entsprechend auch vom richtigen Ergebnis abweicht. Die Größe der Abweichung des Messergebnisses sollte man ebenfalls ausrechnen können (im Rahmen des quantitativ Sinnvollen, siehe Fehlergrenze).

Möglichkeiten, Einschränkungen

Systematischer Fehler

Systematische Fehler sind im Prinzip bestimmbar, sie haben einen Betrag und ein Vorzeichen.

Beispiel: Man will die in einem Verbraucher umgesetzte elektrische Leistung berechnen und dazu den Strom durch den Verbraucher messen. Dazu schaltet man einen Strommesser in die Leitung. An dem Messgerät fällt aber eine Spannung ab; dadurch wird die Spannung am Verbraucher kleiner als die Speisespannung; dadurch wird bei einem ohmschen Verbraucher der Strom auch kleiner; man misst etwas zu wenig (negativer Schaltungseinfluss-Fehler, der sich bei bekannter Speisespannung und bei bekanntem Messgeräte-Innenwiderstand ausrechnen lässt). Die aus Speisespannung und gemessenem Strom berechnete Leistung wird damit auch zu niedrig angegeben.

Bei systematischen Fehlern der Eingangsgrößen lässt sich mittels der Fehlerfortpflanzungs-Regeln der systematische Fehler der Ausgangsgröße berechnen.

Messgerätefehler

Ferner kann man nicht davon ausgehen, dass die vom Messgerät erfasste Größe richtig angezeigt wird. In seltenen Fällen kennt man anhand einer Fehlerkurve zu dem Messwert den zugehörigen systematischen Fehler. Im Allgemeinen kennt man von einem Messgerätefehler nur dessen Grenzwert, die Fehlergrenze.

Beispiel: Kann man den Strom im obigen Beispiel nur mit einer Fehlergrenze von 4 % bestimmen, kann die Fehlergrenze der Leistung nicht niedriger sein.

Bei Fehlergrenzen der Eingangsgrößen lässt sich mittels der Fehlerfortpflanzungs-Regeln die Fehlergrenze der Ausgangsgröße berechnen.

Zufälliger Fehler

Soweit bisher behandelt, hat man mehrere Eingangsgrößen (unabhängige Variable, Messgrößen) und davon jeweils nur einen Wert. Anders ist es bei zufälligen Fehlern, die man erkennt, wenn von einer Eingangsgröße mehrere Werte vorliegen – gewonnen durch wiederholte Bestimmung (Messung) unter konstanten Bedingungen. Die Abschätzung zufälliger Fehler führt auf eine Komponente der Messunsicherheit. Ihre Bestimmung ist ein Ziel der Fehlerrechnung.

Bei Unsicherheiten der Eingangsgrößen lässt sich mittels der Fehlerfortpflanzungs-Regeln die Unsicherheit der Ausgangsgröße berechnen.

Bei Messgerätefehlern kann man gemäß davon ausgehen, dass der Betrag des zufälligen Fehlers wesentlich kleiner ist als die Fehlergrenze (anderenfalls ist auch der zufällige Fehler bei der Festlegung der Fehlergrenze zu berücksichtigen). Bei voneinander unabhängigen Messwerten, deren Qualität von den Fehlergrenzen der Messgeräte bestimmt wird, ist die Untersuchung zufälliger Fehler dann aber nicht sinnvoll.

Fehler des mathematischen Modells

Die zu berechnende Größe muss durch die Formel korrekt beschrieben werden. Um leichter rechnen zu können oder mangels vollständiger Kenntnis weicht man aber oft auf Näherungen aus.

Beispiel: Die Speisespannung im obigen Beispiel wird als bekannt angenommen, wie das bei Bezug aus einer Konstantspannungsquelle zulässig ist. Falls die Quelle aber belastungsabhängig ist, ist ihre Kenngröße „Leerlaufspannung“ nicht mehr die Speisespannung; es entsteht ein weiterer Fehler.

Ein Fehler der Ausgangsgröße, welcher aufgrund fehlerhafter mathematischer Beschreibung des Zusammenhangs mit den Eingangsgrößen entsteht, lässt sich mit Fehlerfortpflanzungs-Regeln nicht berechnen.

Regeln zur Fehlerfortpflanzung

Fehler

Eine fehlerbehaftete Größe

Der Einfluss einer fehlerbehafteten Eingangsgröße $x$ auf das Ergebnis $y$ kann mittels der Taylorreihe abgeschätzt werden:

$y = y(x)\quad \Rightarrow \quad y(x+ \Delta x)= y(x) + \frac{1}{1!}\ \frac{d y(x)}{d x} \cdot \Delta x + \frac{1}{2!}\ \frac{d^2 y(x)}{d x^2}\cdot (\Delta x)^2 + \cdots\$ .

Bei genügend kleinem $|\Delta x|$ kann man die Reihenentwicklung nach dem linearen Glied abbrechen, und man erhält dann die Näherungslösung

$y(x+ \Delta x)- y(x) = \Delta y = \frac{d y}{d x} \cdot \Delta x \; .$

Dieses liefert eine Regel zur Fehlerfortpflanzung, wenn man die $\Delta$-Werte als absolute Fehler ansieht.

• Anwendung bei Proportionalität

$y = c \cdot x \quad \ \Rightarrow \quad \Delta y=c \cdot \Delta x \quad ; \quad \frac{\Delta y}{y} = \frac{\Delta x}{x}$

Für die Ausgangsgröße $y$ enthält deren absoluter Fehler $\Delta y$ die spezielle Proportionalitätskonstante $c$. Besser rechnet man mit dem relativen Fehler $\Delta y/y$, der unabhängig von $c$ ist und stets genauso groß wie der relative Fehler $\Delta x/x$ der Eingangsgröße $x$.

• Anwendung bei umgekehrter Proportionalität (Kehrwertbildung)

$y = \frac cx \quad \quad \Rightarrow \quad \frac{\Delta y}y = -\;\frac{\Delta x}x$

Die Ausgangsgröße hat denselben Betrag des relativen Fehlers wie die Eingangsgröße, aber entgegengesetztes Vorzeichen.

Mehrere fehlerbehaftete Größen

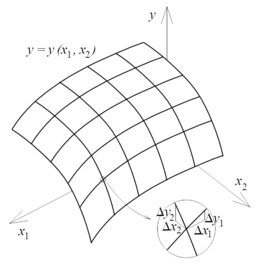
Bei mehreren voneinander unabhängigen Eingangsgrößen verwendet man die entsprechende Reihenentwicklung bis zum linearen Glied als Näherungslösung für kleine $\left|\Delta x_i\right|$ :

$y = y(x_1\,,\ x_2\,,\ \dots \ )\quad \Rightarrow \quad \Delta y = \frac{\partial y}{\partial x_1} \cdot \Delta x_1 + \frac{\partial y}{\partial x_2} \cdot \Delta x_2 +\cdots \$

$\Delta y\$ : Gesamtfehler $F_y$ des Ergebnisses $y$

$\Delta x_i\$ : Fehler $F_i$ der Eingangsgröße $x_i$

$\frac{\Delta x_i}{x_i}$: relativer Fehler $f_i$ der Eingangsgröße $x_i$

$\frac{\Delta y}{y}$ : relativer Fehler $f_y$ des Ergebnisses $y$

Die allgemeine Lösung vereinfacht sich für die vier Grundrechenarten:

* Bei Addition	$y=x_1 +x_2 \quad \quad F_y = F_1 +F_2$
* Bei Subtraktion	$y=x_1 -x_2 \quad \quad F_y = F_1 -F_2$
* Bei Multiplikation	$y=x_1 \cdot x_2 \quad \quad \ \ f_y = f_1 +f_2$
* Bei Division	$y=x_1:x_2 \quad \quad \ \ f_y = f_1 -f_2$

Ausdrücklicher Hinweis: Angaben mit ungewissem Vorzeichen (±) sind keine Angaben von Fehlern; Unterschied zwischen Fehler und Fehlergrenze beachten! Bei Fehlergrenzen und Messunsicherheiten gelten andere Sachverhalte, siehe dazu die nächsten Abschnitte.
Die Formeln gelten nur, wenn die tatsächlichen Werte der Fehler mit Vorzeichen bekannt sind. Bei Fehlerfortpflanzung können sich die Fehler ergänzen oder mehr oder weniger aufheben.

Beispiel: Wenn $x_1$ um 2 % zu groß und $x_2$ um 3 % zu groß sind:

Dann wird bei der Multiplikation $y$ um 5 % zu groß.

Dann wird bei der Division $y$ um 1 % zu klein.

Zur Verdeutlichung eine Primitiv-Anwendung: Wer $\tfrac{1{,}00}{1{,}00}$ ausrechnen will, aber im Zähler eine um 2 % zu große Zahl einsetzt und im Nenner eine um 3 % zu große Zahl, berechnet $\tfrac{1{,}02}{1{,}03}$ und erhält 0,99. Dieses Ergebnis weicht vom richtigen Wert 1,00 um –1 % ab. Diese Feststellung zum Fehler kann man mit der Formel
$f_y =f_1 -f_2$ = 2 % - 3 %     einfacher bekommen. Und das Minuszeichen vor $f_2$ ist offensichtlich richtig!

Fehlergrenzen

Kennt man nicht die Fehler selber, sondern nur ihre Grenzen, so lässt sich derselbe mathematische Ansatz verwenden, wenn man die $\Delta$-Werte als Fehlergrenzen ansieht. Diese sind vorzeichenlos bzw. als Betrag definiert. Für das Ergebnis lässt sich so auch nur die Fehlergrenze ausrechnen; dazu muss man mit der ungünstigsten Vorzeichenkombination rechnen und Beträge addieren.

$\Delta y = \left| \frac{\partial y}{\partial x_1} \right| \cdot \Delta x_1+ \left|\frac{\partial y}{\partial x_2} \right| \cdot \Delta x_2 + \cdots \$

$\Delta y\$ : Gesamtfehlergrenze $G_y$ des Ergebnisses $y$

$\Delta x_i\$ : Fehlergrenze $G_i$ der Eingangsgröße $x_i$

$\frac{\Delta x_i}{\left|x_i \right|}$: relative Fehlergrenze $g_i$ der Eingangsgröße $x_i$

$\frac{\Delta y}{\left|y\right|}$ : relative Fehlergrenze $g_y$ des Ergebnisses $y$

Die allgemeine Lösung vereinfacht sich bei den vier Grundrechenarten:

* Bei Addition und Subtraktion	$G_y = G_1 +G_2$
* Bei Multiplikation und Division	$g_y\ =g_1 +g_2$

Beispiel: Wenn $x_1$ um bis 2 % zu groß oder zu klein und $x_2$ um bis 3 % zu groß oder zu klein sein können:

Dann kann bei der Multiplikation wie bei der Division $y$ um bis 5 % zu groß oder zu klein sein.

Messunsicherheiten

Eine fehlerbehaftete Größe

Hat man von der Größe $x$ mehrere mit zufälligen Fehlern behaftete Werte $v_j$ mit $j=1 \cdots N$, so bekommt man nach den Regeln der Fehlerrechnung für Normalverteilung gegenüber dem Einzelwert zu einer verbesserten Aussage durch Bildung des arithmetischen Mittelwertes $\overline {v_x}$:

$\overline{v_x}=\frac1N \sum_{j=1}^N v_j$

Jeder neu hinzukommende Wert verändert mit seinem individuellen zufälligen Fehler den Mittelwert und macht ihn somit unsicher. Die Unsicherheit $u_x$ , die dem berechneten Mittelwert anhaftet, ist gegeben durch:

$u_x = \sqrt {\frac1{N(N-1)} \sum_{j=1}^N (v_j-\overline{v_x})^2}$

Anschaulich sind hier näherungsweise die quadrierten zufälligen Fehler addiert worden. Für große $N$ strebt die Unsicherheit gegen null, und bei Abwesenheit systematischer Fehler strebt der Mittelwert gegen den richtigen Wert.

Verwendet man in einer Rechnung zur Fehlerfortpflanzung als Eingangsgröße $x$ den Mittelwert $\overline {v_x}$ , so wirkt sich dessen Unsicherheit $u_x$ auf die Unsicherheit $u_y$ des Ergebnisses $y$ aus. Bei genügend kleinem $u_x$ kann dieser Wert für die Fehlerfortpflanzung als $\Delta x$ in die lineare Näherung der Taylorreihe eingesetzt werden. Dabei muss man beachten, dass Unsicherheiten als Beträge definiert sind:

$\Delta y = \frac{dy}{dx} \cdot \Delta x \qquad \qquad \Rightarrow \qquad \qquad u_y =\left| \frac{dy}{dx} \right| \cdot u_x$

Mehrere fehlerbehaftete Größen

Voneinander unabhängige fehlerbehaftete Größen

Bei mehreren voneinander unabhängigen Eingangsgrößen $x_1 \,,\ x_2 \,,\ \cdots\$ seien die Mittelwerte jeweils mit einer Unsicherheit $u_1 \,,\ u_2 \,,\ \cdots\$ bestimmt worden. Das Ergebnis $y$ wird aus den Mittelwerten berechnet. Zur Berechnung seiner Unsicherheit $u_y$ beginnt man wieder mit der linearen Näherung bei mehreren unabhängigen Variablen; allerdings muss man – wie bei der Berechnung der Unsicherheit – die quadrierten Beiträge der Einzel-Unsicherheiten addieren.

$\Delta y = \frac{\partial y}{\partial x_1} \cdot \Delta x_1 + \frac{\partial y}{\partial x_2} \cdot \Delta x_2 +\cdots \ \Rightarrow \ {u_y}=\sqrt {\left (\frac{\partial y}{\partial x_1} \cdot u_1 \right)^2 +\left (\frac{\partial y}{\partial x_2} \cdot u_2 \right)^2 +\cdots }$

Diese Gleichung „wurde früher "Fehlerfortpflanzungsgesetz" genannt“ (Gauß'sches Fehlerfortpflanzungsgesetz). „Sie betrifft jedoch nicht die Fortpflanzung von Messabweichungen (früher "Fehler"), sondern die von Unsicherheiten.“

Die Gleichung vereinfacht sich für die vier Grundrechenarten:

* Bei Addition und Subtraktion	$y=x_1 +x_2-x_3 \qquad \quad {u_y}^2= {u_1}^2 +{u_2}^2+{u_3}^2$
* Bei Multiplikation und Division	$y=x_1 \cdot x_2:x_3 \qquad \left(\frac{u_y}y\right)^2 =\left(\frac{u_1}{x_1}\right)^2 +\left(\frac{u_2}{x_2}\right)^2 +\left(\frac{u_3}{x_3}\right)^2$

Das Gesetz ist nur anwendbar, wenn sich die Modellfunktion $y= y(x_1 \,,\ x_2 \,,\ \cdots)$ bei Änderungen der Einflussgrößen $x_i$ im Bereich ihrer Standardunsicherheiten $u_i$ hinreichend linear verhält. Ist dies nicht der Fall, ist das Rechenverfahren erheblich aufwändiger. Die Norm DIN 1319 und der „Leitfaden zur Angabe der Unsicherheit beim Messen“ geben Hinweise, wie eine unzulässige Nichtlinearität zu erkennen und zu umgehen ist. Außerdem ist Varianzhomogenität vorausgesetzt.

Voneinander abhängige fehlerbehaftete Größen

Bei einer Abhängigkeit (Korrelation) zwischen $m$ fehlerbehafteten Größen muss das Gauß'sche Fehlerfortpflanzungsgesetz unter Einbeziehung der Kovarianzen oder der Korrelationskoeffizienten zwischen jeweils zwei Größen zum verallgemeinerten (generalisierten) Gauß'schen Fehlerfortpflanzungsgesetz erweitert werden:

$u_y=\sqrt{\underbrace{\sum_{i=1}^m\left(\frac{\partial y}{\partial x_i}\cdot u_i\right)^2}_{\mathrm{wie~oben}}+ 2\underbrace{\sum_{i=1}^{m-1}\sum_{k=i+1}^m\left(\frac{\partial y}{\partial x_i}\right)\left(\frac{\partial y}{\partial x_k}\right)\cdot u(x_i, x_k)}_{\mathrm{Korrelationsterme}}}$

mit der Kovarianz $u (x_i, x_k)$ . Für unabhängige Größen fallen die Korrelationsterme weg und es ergibt sich die Formel aus dem Abschnitt für unabhängige Größen.

Die relative Unsicherheit einer Größe, die sich aus zwei vollkommen korrelierten Größen ableitet, kann dabei kleiner (besser) werden als die beiden relativen Unsicherheiten der Eingangsgrößen.