Korrelationskoeffizient nach Bravais-Pearson
Der Korrelationskoeffizient nach Bravais-Pearson, auch Produkt-Moment-Korrelation,[1] ist ein Maß für den Grad des linearen Zusammenhangs zwischen zwei mindestens intervallskalierten Merkmalen, das nicht von den Maßeinheiten der Messung abhängt und somit dimensionslos ist. Er kann Werte zwischen und annehmen. Bei einem Wert von (bzw. ) besteht ein vollständig positiver (bzw. negativer) linearer Zusammenhang zwischen den betrachteten Merkmalen. Wenn der Korrelationskoeffizient den Wert 0 aufweist, hängen die beiden Merkmale überhaupt nicht linear voneinander ab. Allerdings können diese ungeachtet dessen in nichtlinearer Weise voneinander abhängen. Damit ist der Korrelationskoeffizient kein geeignetes Maß für die (reine) stochastische Abhängigkeit von Merkmalen. Das Quadrat des Korrelationskoeffizienten stellt das Bestimmtheitsmaß dar. Der Korrelationskoeffizient wurde erstmals vom britischen Naturforscher Sir Francis Galton (1822–1911) in den 1870er Jahren verwendet. Karl Pearson lieferte schließlich eine formal-mathematische Begründung für den Korrelationskoeffizienten.[2] Da er von Auguste Bravais und Pearson populär gemacht wurde, wird der Korrelationskoeffizient auch Pearson-Korrelation oder Bravais-Pearson-Korrelation genannt.
Je nachdem, ob der lineare Zusammenhang zwischen zeitgleichen Messwerten zweier verschiedener Merkmale oder derjenige zwischen zeitlich verschiedenen Messwerten eines einzigen Merkmals betrachtet wird, spricht man entweder von der Kreuzkorrelation oder von der Kreuzautokorrelation (siehe auch Zeitreihenanalyse).
Korrelationskoeffizienten wurden mehrfach – so schon von Ferdinand Tönnies – entwickelt, heute wird allgemein jener von Pearson verwendet.
Definitionen[Bearbeiten | Quelltext bearbeiten]
Korrelationskoeffizient für Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Konstruktion[Bearbeiten | Quelltext bearbeiten]
Als Ausgangspunkt für die Konstruktion des Korrelationskoeffizienten für zwei Zufallsvariablen und betrachtet man die beiden standardisierten (auf die Standardabweichung bezogenen) Zufallsvariablen und . Die Kovarianz dieser standardisierten Zufallsvariablen ergibt sich aus dem Satz für lineare Transformationen von Kovarianzen zu
- .
Der Korrelationskoeffizient lässt sich als die Kovarianz der standardisierten Zufallsvariablen und auffassen.[3]
Definition[Bearbeiten | Quelltext bearbeiten]
Für zwei quadratisch integrierbare Zufallsvariablen und mit jeweils positiver Standardabweichung bzw. und Kovarianz ist der Korrelationskoeffizient (Pearsonscher Maßkorrelationskoeffizient) definiert durch:
- .
Dieser Korrelationskoeffizient wird auch Korrelationskoeffizient der Grundgesamtheit genannt. Durch die Definitionen der stochastischen Varianz und Kovarianz lässt sich der Korrelationskoeffizient für Zufallsvariablen auch wie folgt darstellen:[4]
wobei den Erwartungswert darstellt.
Ferner heißen unkorreliert, falls gilt. Für positive und ist das genau dann der Fall, wenn ist. Sind unabhängig, so sind sie auch unkorreliert, die Umkehrung gilt im Allgemeinen nicht.
Schätzung[Bearbeiten | Quelltext bearbeiten]
Im Rahmen der induktiven Statistik ist man an einer erwartungstreuen Schätzung des Korrelationskoeffizienten der Grundgesamtheit interessiert. Daher werden in die Formel des Korrelationskoeffizienten der Grundgesamtheit erwartungstreue Schätzer der Varianzen und der Kovarianz eingesetzt. Dies führt zum Stichprobenkorrelationskoeffizienten:
Empirischer Korrelationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Sei eine zweidimensionale Stichprobe zweier kardinalskalierter Merkmale mit den empirischen Mitteln und der Teilstichproben und . Weiterhin gelte für die empirischen Varianzen und der Teilstichproben . Dann ist der empirische Korrelationskoeffizient – analog zum Korrelationskoeffizienten für Zufallsvariablen, nur dass man statt der theoretischen Momente nun die empirische Kovarianz und die empirischen Varianzen verwendet – definiert durch:[5]

Hierbei ist die Summe der Abweichungsquadrate und die Summe der Abweichungsprodukte.
Mithilfe der empirischen Kovarianz und den empirischen Standardabweichungen
- und
der Teilstichproben und ergibt sich die folgende Darstellung:
Sind diese Messreihenwerte z-transformiert, das heißt, , wobei die erwartungstreue Schätzung der Varianz bezeichnet, gilt auch:
Da man in der deskriptiven Statistik nur den Zusammenhang zwischen zwei Variablen als normierte mittlere gemeinsame Streuung in der Stichprobe beschreiben will, wird die Korrelation auch berechnet als
- .
Da sich die Faktoren bzw. aus den Formeln herauskürzen, ergibt sich in beiden Fällen der gleiche Wert des Koeffizienten.
Eine „Vereinfachung“ der obigen Formel zur leichteren Berechnung einer Korrelation lautet wie folgt:[6]
Diese Transformation der Formel ist aber numerisch instabil und sollte daher nicht mit Gleitkommazahlen verwendet werden, wenn die Mittelwerte nicht nahe null sind.[7]
Beispiel[Bearbeiten | Quelltext bearbeiten]

Für die elf Beobachtungspaare sind die Werte in der unten stehenden Tabelle in der zweiten und dritten Spalte gegeben. Die Mittelwerte ergeben sich zu und und damit können die vierte und fünfte Spalte der Tabelle berechnet werden. Die sechste Spalte enthält das Produkt der vierten mit der fünften Spalte und damit ergibt sich . Die beiden letzten Spalten enthalten jeweils die Quadrate der vierten und fünften Spalte und es ergibt sich und .
Damit ergibt sich für die Korrelation .
| 1 | 10,00 | 8,04 | 1,00 | 0,54 | 0,54 | 1,00 | 0,29 |
| 2 | 8,00 | 6,95 | −1,00 | −0,55 | 0,55 | 1,00 | 0,30 |
| 3 | 13,00 | 7,58 | 4,00 | 0,08 | 0,32 | 16,00 | 0,01 |
| 4 | 9,00 | 8,81 | 0,00 | 1,31 | 0,00 | 0,00 | 1,71 |
| 5 | 11,00 | 8,33 | 2,00 | 0,83 | 1,66 | 4,00 | 0,69 |
| 6 | 14,00 | 9,96 | 5,00 | 2,46 | 12,30 | 25,00 | 6,05 |
| 7 | 6,00 | 7,24 | −3,00 | −0,26 | 0,78 | 9,00 | 0,07 |
| 8 | 4,00 | 4,26 | −5,00 | −3,24 | 16,20 | 25,00 | 10,50 |
| 9 | 12,00 | 10,84 | 3,00 | 3,34 | 10,02 | 9,00 | 11,15 |
| 10 | 7,00 | 4,82 | −2,00 | −2,68 | 5,36 | 4,00 | 7,19 |
| 11 | 5,00 | 5,68 | −4,00 | −1,82 | 7,28 | 16,00 | 3,32 |
| 99,00 | 82,51 | 55,01 | 110,00 | 41,27 | |||
| Alle Werte in der Tabelle sind auf zwei Stellen nach dem Komma gerundet! | |||||||
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Mit der Definition des Korrelationskoeffizienten gilt unmittelbar
- bzw.
Dabei sind und reelle Zahlen (mit wegen der definitorisch vorausgesetzten Positivität der Varianz von ) und ist die Signumfunktion.[8]
Aus der Cauchy-Schwarzschen Ungleichung folgt
- .
Man erkennt:
- fast sicher genau dann, wenn
Das lässt sich zum Beispiel durch Lösen der Gleichung einsehen. In dem Fall ist und .
Sind die Zufallsgrößen und stochastisch voneinander unabhängig, dann gilt:
Der Umkehrschluss ist allerdings nicht zulässig, denn es können Abhängigkeitsstrukturen vorliegen, die der Korrelationskoeffizient nicht erfasst. Für die multivariate Normalverteilung gilt jedoch: Die Zufallsvariablen und sind genau dann stochastisch unabhängig, wenn sie unkorreliert sind. Wichtig ist hierbei die Voraussetzung, dass und gemeinsam normalverteilt sind. Es reicht nicht aus, dass sowohl als auch normalverteilt sind.
Voraussetzungen für die Pearson-Korrelation[Bearbeiten | Quelltext bearbeiten]
Der Korrelationskoeffizient nach Pearson erlaubt Aussagen über statistische Zusammenhänge unter folgenden Bedingungen:
Skalierung[Bearbeiten | Quelltext bearbeiten]
Der Pearsonsche Korrelationskoeffizient liefert korrekte Ergebnisse bei intervallskalierten und bei dichotomen Daten. Für niedrigere Skalierungen existieren andere Korrelationskonzepte (z. B. Rangkorrelationskoeffizienten).
Normalverteilung[Bearbeiten | Quelltext bearbeiten]
Für die Durchführung von standardisierten Signifikanztests über den Korrelationskoeffizienten in der Grundgesamtheit müssen beide Variablen annähernd normalverteilt sein. Bei zu starken Abweichungen von der Normalverteilung muss auf den Rangkorrelationskoeffizienten zurückgegriffen werden. (Alternativ kann man auch, falls die Verteilung bekannt ist, angepasste (nichtstandardisierte) Signifikanztests verwenden.)
Linearitätsbedingung[Bearbeiten | Quelltext bearbeiten]
Zwischen den Variablen und wird ein linearer Zusammenhang vorausgesetzt. Diese Bedingung wird in der Praxis häufig ignoriert; daraus erklären sich mitunter enttäuschend niedrige Korrelationen, obwohl der Zusammenhang zwischen und bisweilen trotzdem hoch ist. Ein einfaches Beispiel für einen hohen Zusammenhang trotz eines niedrigen Korrelationskoeffizienten ist die Fibonacci-Folge. Alle Zahlen der Fibonacci-Folge sind durch ihre Position in der Reihe durch eine mathematische Formel exakt determiniert (siehe die Formel von Binet). Der Zusammenhang zwischen der Positionsnummer einer Fibonacci-Zahl und der Größe der Zahl ist vollkommen determiniert. Dennoch beträgt der Korrelationskoeffizient zwischen den Ordnungsnummern der ersten 360 Fibonacci-Zahlen und den betreffenden Zahlen nur 0,20; das bedeutet, dass in erster Näherung nicht viel mehr als der Varianz durch den Korrelationskoeffizienten erklärt werden und 96 % der Varianz „unerklärt“ bleiben. Der Grund ist die Vernachlässigung der Linearitätsbedingung, denn die Fibonacci-Zahlen wachsen progressiv an: In solchen Fällen ist der Korrelationskoeffizient nicht korrekt interpretierbar. Eine mögliche Alternative, die ohne die Voraussetzung der Linearität des Zusammenhangs auskommt, ist die Transinformation.
Signifikanzbedingung[Bearbeiten | Quelltext bearbeiten]
Ein Korrelationskoeffizient > 0 bei positiver Korrelation bzw. < 0 bei negativer Korrelation zwischen und berechtigt nicht a priori zur Aussage, es bestehe ein statistischer Zusammenhang zwischen und . Eine solche Aussage ist nur gültig, wenn der ermittelte Korrelationskoeffizient signifikant ist. Der Begriff „signifikant“ bedeutet hier „signifikant von Null verschieden“. Je höher die Anzahl der Wertepaare und das Signifikanzniveau sind, desto niedriger darf der Absolutbetrag eines Korrelationskoeffizienten sein, um zur Aussage zu berechtigen, zwischen und gebe es einen linearen Zusammenhang. Ein t-Test zeigt, ob die Abweichung des ermittelten Korrelationskoeffizienten von Null auch signifikant ist.
Bildliche Darstellung und Interpretation[Bearbeiten | Quelltext bearbeiten]
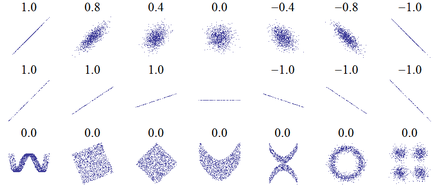
Sind zwei Merkmale vollständig miteinander korreliert (d. h. ), so liegen alle Messwerte in einem 2-dimensionalen Koordinatensystem auf einer Geraden. Bei einer perfekten positiven Korrelation () steigt die Gerade. Wenn die Merkmale perfekt negativ miteinander korreliert sind (), sinkt die Gerade. Besteht zwischen zwei Merkmalen eine sehr hohe Korrelation, sagt man oft auch, sie erklären dasselbe.
Je näher der Betrag von bei 0 liegt, desto kleiner der lineare Zusammenhang. Für kann der statistische Zusammenhang zwischen den Messwerten nicht mehr durch eine eindeutig steigende oder sinkende Gerade dargestellt werden. Dies ist z. B. der Fall, wenn die Messwerte rotationssymmetrisch um den Mittelpunkt verteilt sind. Dennoch kann dann ein nichtlinearer statistischer Zusammenhang zwischen den Merkmalen gegeben sein. Umgekehrt gilt jedoch: Wenn die Merkmale statistisch unabhängig sind, nimmt der Korrelationskoeffizient stets den Wert 0 an.
Korrelation: Koinzidenz oder Kausalzusammenhang
In der Monographie „Kontrazeption mit Hormonen“ von Hans-Dieter Taubert und Herbert Kuhl (Abteilung für gynäkologische Endokrinologie, Zentrum der Frauenheilkunde und Geburtshilfe der J.W. Goethe-Universität), die 1981 im Georg Thieme Verlag Stuttgart erschien, wurde das Problem der Bedeutung von Korrelationen bei medizinischen Studien angesprochen. Es ist bekannt, dass Korrelationen (z. B. zwischen Hormondosierungen oder -serumkonzentrationen und dem Auftreten bestimmter Erkrankungen), die bei solchen Untersuchungen ermittelt werden, häufig als Beleg für einen Kausalzusammenhang interpretiert werden. Unabhängig von den zahlreichen methodischen Problemen solcher Studien werden selbst offensichtlich fragwürdige Ergebnisse gerne von den Medien kolportiert.
In dem Abschnitt „Aussagekraft verschiedener Untersuchungskonzepte“ wurde auf den Seiten 207–208 (in der 2. Auflage von 1995 auf den Seiten 239–240) als Beispiel die Bedeutung einer extrem engen Korrelation zwischen der Zahl der Storchenpaare und der Geburtenzahl in der Bevölkerung in Baden-Württemberg in dem Zeitraum zwischen 1966 und 1975 diskutiert. Aus den Daten über die kontinuierliche Abnahme der Storchenpopulation, die dem Journal für Ornithologie von 1979 entnommen wurden und dem Rückgang der Geburtenrate, der sich aus den Zahlen des Statistischen Jahrbuchs der Bundesrepublik Deutschland ergab, wurden
- die Regressionsgerade mit und
- der Korrelationskoeffizient mit berechnet ().
Das Ergebnis ist in Abb. 46 auf S. 208 (bzw. in Abb. 60 auf S. 240 der 2. Auflage 1995) dargestellt. In dem begleitenden Text ist u. a. zu lesen: „Grundsätzlich sollten alle Aussagen über vermutete Zusammenhänge zwischen der Anwendung hormonaler Kontrazeptiva und dem Auftreten bestimmter Erkrankungen aus dem Blickwinkel erfolgen, dass die Wahrscheinlichkeit einer zufälligen Koinzidenz mit der Häufigkeit der Vergleiche steigt. So konnte mit Hilfe kontrollierter prospektiver Untersuchungen in vielen Fällen nachgewiesen werden, dass sich die Häufigkeit bestimmter Erkrankungen bei Einnahme von Ovulationshemmern nicht von der in der Gesamtbevölkerung unterscheidet. Andererseits bedeutet selbst eine hoch signifikante Korrelation zwischen zwei Parametern noch keinen Kausalzusammenhang, auch wenn dieser plausibel erscheint. Dies sei anhand der Beobachtung demonstriert, dass die Zahl der Storchenpaare in Baden-Württemberg von 67 im Jahre 1965 auf 15 im Jahre 1975 abnahm und gleichzeitig die Geburtenzahl in diesem Bundesland von 159.000 auf 97.000 zurück ging (s. Abb.). Zwischen beiden Parametern wurde eine Korrelation ermittelt, die hoch signifikant () ist. Trotzdem wäre es voreilig, daraus zu schließen, dass für den Geburtenrückgang die Abnahme der Storchenpopulation kausal verantwortlich ist.“ Übrigens ist zur Frage der Plausibilität anzumerken, dass diese grundsätzlich vom aktuellen Kenntnisstand abhängig ist.

Der Korrelationskoeffizient ist kein Indiz eines ursächlichen (d. h. kausalen) Zusammenhangs zwischen den beiden Merkmalen: Die Besiedlung durch Störche im Südburgenland korreliert zwar positiv mit der Geburtenzahl der dortigen Einwohner, doch das bedeutet noch keinen „kausalen Zusammenhang“, trotzdem ist ein „statistischer Zusammenhang“ gegeben. Dieser leitet sich aber aus einem anderen, weiteren Faktor ab, wie dies im Beispiel durch Industrialisierung oder der Wohlstandssteigerung begründet sein kann, die einerseits den Lebensraum der Störche einschränkten und andererseits zu einer Verringerung der Geburtenzahlen führten. Korrelationen dieser Art werden Scheinkorrelationen genannt.
Der Korrelationskoeffizient kann kein Indiz über die Richtung eines Zusammenhanges sein: Steigen die Niederschläge durch die höhere Verdunstung oder steigt die Verdunstung an, weil die Niederschläge mehr Wasser liefern? Oder bedingen sich beide gegenseitig, also möglicherweise in beiderlei Richtung?
Ob ein gemessener Korrelationskoeffizient als groß oder klein interpretiert wird, hängt stark von der Art der untersuchten Daten ab. Bei psychologischen Untersuchungen gelten Werte ab als kleine, als mittlere und als große Effekte.[9][10]
Das Quadrat des Korrelationskoeffizienten nennt man Bestimmtheitsmaß. Es gibt in erster Näherung an, wie viel Prozent der Varianz (d. h. des Streuungsquadrats), der einen Variable durch die Varianz der anderen Variable erklärt werden können. Beispiel: Bei werden 9 % () der gesamten auftretenden Varianz im Hinblick auf einen statistischen Zusammenhang erklärt.
Allgemeiner empirischer Korrelationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Der empirische Pearson-Korrelationskoeffizient bedingt, wie oben erwähnt, einen linearen Zusammenhang, um brauchbare Werte zu liefern. Es existiert jedoch auch ein allgemeiner empirischer Korrelationskoeffizient, der für jede beliebige Funktion brauchbare Werte liefert:
Der Bruch unter der Wurzel entspricht dem empirischen Bestimmtheitsmaß . Für den Spezialfall einer linearen Funktion geht der allgemeine empirische Korrelationskoeffizient wieder in den empirischen Pearson-Korrelationskoeffizienten über.
Fisher-Transformation[Bearbeiten | Quelltext bearbeiten]
Empirische Korrelationskoeffizienten sind nicht normalverteilt. Vor der Berechnung von Konfidenzintervallen muss daher erst eine Korrektur der Verteilung mit Hilfe der Fisher-Transformation vorgenommen werden. Wenn die Daten und aus einer zumindest annähernd bivariat normalverteilten Grundgesamtheit stammen, dann ist der empirische Korrelationskoeffizient rechtssteil unimodal verteilt.
Die Fisher-Transformation des Korrelationskoeffizienten lautet dann
ist annähernd normalverteilt mit der Standardabweichung und Mittelwert
wobei hier für den Korrelationskoeffizienten der Grundgesamtheit steht. Die auf Basis dieser Normalverteilung errechnete Wahrscheinlichkeit, dass der Mittelwert von den beiden Grenzen und umschlossen wird beträgt
und wird sodann retransformiert zu
Das -Konfidenzintervall für die Korrelation lautet sodann
- .
Konfidenzintervalle von Korrelationen liegen in aller Regel unsymmetrisch bezüglich ihres Mittelwerts.
Test des Korrelationskoeffizienten / Steigers Z-Test[Bearbeiten | Quelltext bearbeiten]
Folgende Tests (Steigers Z-Test)[11] können durchgeführt werden, wenn die Variablen und annähernd bivariat normalverteilt sind:
| vs. | (zweiseitige Hypothese) |
| vs. | (rechtsseitige Hypothese) |
| vs. | (linksseitige Hypothese) |
Die Teststatistik
ist standardnormalverteilt ( ist die Fisher-Transformation, siehe vorherigen Abschnitt).
Im Spezialfall der Hypothese vs. ergibt sich die Teststatistik als t-verteilt mit Freiheitsgraden:
Matthews Korrelationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Betrachtet man zwei binäre Variablen X und Y, so ist der Pearson-Korrelationskoeffizient dieser Variablen
und kann direkt aus der Konfusionsmatrix berechnet werden, wobei in der 2×2 Konfusionsmatrix
| y = 1 | y = 0 | total | |
| x = 1 | |||
| x = 0 | |||
| total |
n11, n10, n01, n00, die nicht negativen absoluten Häufigkeiten der Beobachtungen sind (deren Summe die Zahl der Beobachtungen n ist). Dieser Wert ist auch als Mathews Korrelationskoeffizient (MCC) bekannt und kann unter Umständen numerisch schneller berechenbar sein.
Partieller Korrelationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Die partielle Korrelation kontrolliert den Einfluss von Störvariablen.
Robuste Korrelationskoeffizienten[Bearbeiten | Quelltext bearbeiten]
Der Korrelationskoeffizient nach Pearson ist empfindlich gegenüber Ausreißern. Deswegen wurden verschiedene robuste Korrelationskoeffizienten entwickelt, z. B.
- Rangkorrelationskoeffizienten, die Ränge statt der Beobachtungswerte nutzen (wie der Spearman’sche Rangkorrelationskoeffizient (Spearman’sches Rho) und der Kendall’sche Rangkorrelationskoeffizient (Kendall’sches Tau)) oder
- die Quadrantenkorrelation.
Quadrantenkorrelation[Bearbeiten | Quelltext bearbeiten]
Die Quadrantenkorrelation ergibt sich aus der Anzahl der Beobachtungen in den vier vom Medianenpaar bestimmten Quadranten. Dazu zählt man, wie viele der Beobachtungen in den Quadranten I und III liegen () bzw. wie viele sich in den Quadranten II und IV befinden (). Die Beobachtungen in den Quadranten I und III liefern jeweils einen Beitrag von und die Beobachtungen in den Quadranten II und IV von :
mit der Signumfunktion , der Zahl der Beobachtungen sowie den Medianen und der Beobachtungen. Da jeder Wert von entweder , oder ist, spielt es keine Rolle, wie weit eine Beobachtung von den Medianen entfernt ist.
Über die Quadrantenkorrelation kann mit Hilfe des Median-Tests die Hypothesen vs. überprüft werden. Ist die Zahl der Beobachtungen mit , die Zahl der Beobachtungen mit und , dann ist folgende Teststatistik Chi-Quadrat-verteilt mit einem Freiheitsgrad von
- .
Schätzung der Korrelation zwischen nicht-metrischen Variablen[Bearbeiten | Quelltext bearbeiten]
Die Schätzung der Korrelation mit dem Korrelationskoeffizienten nach Pearson setzt voraus, dass beide Variablen intervallskaliert und normalverteilt sind. Dagegen können die Rangkorrelationskoeffizienten immer dann zur Schätzung der Korrelation verwendet werden, wenn beide Variablen mindestens ordinalskaliert sind. Die Korrelation zwischen einer dichotomen und einer intervallskalierten und normalverteilten Variablen kann mit der punktbiserialen Korrelation geschätzt werden. Die Korrelation zwischen zwei dichotomen Variablen kann mit dem Vierfelderkorrelationskoeffizienten geschätzt werden. Hier kann man die Unterscheidung treffen, dass bei zwei natürlich dichotomen Variablen die Korrelation sowohl durch das Chancenverhältnis als auch durch den Phi-Koeffizient berechnet werden kann. Eine Korrelation aus zwei ordinal- oder einer intervall- und einer ordinal-gemessenen Variablen ist mit dem Spearman’schen Rho oder dem Kendall’schen Tau berechenbar.
Multipler Korrelationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Der multiple Korrelationskoeffizient ist eine multivariate Verallgemeinerung des Korrelationskoeffizienten nach Bravais-Pearson.
Probleme[Bearbeiten | Quelltext bearbeiten]
Das Anscombe-Quartett zeigt Datensätze mit exakt gleichem Korrelationskoeffizient, aber sehr unterschiedlichem Verhalten. Auch andere Probleme sind in der Literatur bekannt[12].
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Francis Galton: Co-relations and their measurement, chiefly from anthropometric data. In: Proceedings of the Royal Society. Band 45, Nr. 13, 5. Dezember 1888, S. 135–145 (galton.org [PDF; 468 kB; abgerufen am 26. November 2021]).
- Birk Diedenhofen, Jochen Musch: cocor A Comprehensive Solution for the Statistical Comparison of Correlations. 2015. PLoS ONE, 10(4): e0121945.
- Joachim Hartung: Statistik. 12. Auflage, Oldenbourg Verlag 1999, S. 561 f., ISBN 3-486-24984-3.
- Peter Zöfel: Statistik für Psychologen. Pearson Studium 2003, München, S. 154.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Umfassende Erläuterung verschiedener Korrelationskoeffizienten und ihrer Voraussetzungen, sowie häufige Anwendungsfehler
- Eric W. Weisstein: Correlation Coefficient. In: MathWorld (englisch). Darstellung des Korrelationskoeffizienten als Kleinste-Quadrate-Schätzer
- cocor – Ein freies Web-Interface und R-Paket zum statistischen Vergleich von zwei abhängigen oder unabhängigen Korrelationen mit überlappenden oder nicht überlappenden Variablen
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Der Name Produkt-Moment-Korrelation für den Korrelationskoeffizienten für Zufallsvariablen rührt daher, dass die auf das Produkt der Varianzen – die im Sinne der Stochastik Momente darstellen – von und bezogene Kovarianz ist.
- ↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt. Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 116.
- ↑ L. Fahrmeir, R. Künstler u. a.: Statistik. Der Weg zur Datenanalyse. 8. Auflage. Springer 2016, S. 326.
- ↑ Bayer, Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik, S. 86.
- ↑ Torsten Becker u. a.: Stochastische Risikomodellierung und statistische Methoden. Springer Spektrum, 2016. S. 79.
- ↑ Jürgen Bortz, Christof Schuster: Statistik für Human- und Sozialwissenschaftler. 7. Auflage. Springer-Verlag GmbH, Berlin / Heidelberg / New York 2010, ISBN 978-3-642-12769-4, S. 157.
- ↑ Erich Schubert, Michael Gertz: Numerically stable parallel computation of (co-)variance. ACM, 2018, ISBN 978-1-4503-6505-5, S. 10, doi:10.1145/3221269.3223036 (acm.org [abgerufen am 26. November 2021]).
- ↑ Für alle und gilt:
- ↑ Jacob Cohen: A power primer. In: Psychological Bulletin. Band 112, Nr. 1, 1992, ISSN 1939-1455, S. 155–159, doi:10.1037/0033-2909.112.1.155 (apa.org [abgerufen am 26. November 2021]).
- ↑ Jacob Cohen: A power primer. (PDF; 800 kB) In: personal.kent.edu. 1991, abgerufen am 26. November 2021 (englisch).
- ↑ J. H. Steiger: Tests for comparing elements of a correlation matrix. 1980. Psychological Bulletin, 87, 245–251, doi:10.1037/0033-2909.87.2.245.
- ↑ Aggarwal, Rakesh, and Priya Ranganathan. "Common pitfalls in statistical analysis: The use of correlation techniques." Perspectives in clinical research 7.4 (2016): 187. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5079093/












































![{\displaystyle r_{x,y}={\frac {n\sum _{i=1}^{n}(x_{i}\cdot y_{i})-(\sum _{i=1}^{n}x_{i})\cdot (\sum _{i=1}^{n}y_{i})}{\sqrt {\left[n\sum _{i=1}^{n}x_{i}^{2}-(\sum _{i=1}^{n}x_{i})^{2}\right]\cdot \left[n\sum _{i=1}^{n}y_{i}^{2}-(\sum _{i=1}^{n}y_{i})^{2}\right]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d53a7c600d83cbc1f92abc0bc130787a559784f)

























![{\displaystyle \operatorname {Korr} (X,Y)\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52adb3ec1b330e0858bd899d62813a8ed7b6e1e0)




















































































