Fuzzy-Regler

Übersichtsdarstellung der fuzzifizierten Eingangsgrößen und der Ausgangsgrößen des Fuzzy-Controllers.

Ein Fuzzy-Regler ist ein Regler, der auf der Fuzzylogik basiert. Die Fuzzylogik kommt vorzugsweise dann zur Anwendung, wenn ein technischer Prozess mit mehreren Ein- und Ausgangsgrößen bei stark wechselnden Parametern und nichtlinearen Teilsystemen möglichst ohne menschlichen Eingriff (Anlagenfahrer) gesteuert werden soll.

Im systemanalytischen Sinne ist ein Fuzzy Control System ein statisches nichtlineares Steuersystem, welches aus scharfen Eingangsgrößen eines komplexen Prozesses nach den Regeln einer Regelbasis unscharf definierte fuzzifizierte Steuergrößen und scharfe defuzzifizierte Wertesignale bildet, mit denen ein zufriedenstellendes Prozessergebnis erreicht wird.

Unter der Fuzzifizierung einer scharfen physikalischen Eingangsgröße (Messwert) eines technischen Prozesses versteht man die Quantifizierung durch unscharfe Definitionen mit linguistischen Begriffen wie warm, kalt, viel, wenig, mehr, groß, klein. Über die sogenannten graphischen trapez- oder dreieckförmige Fuzzy-Sets werden die Zugehörigkeitsgrade $\mu _{i}$ aus den scharfen Eingangssignalen innerhalb der Grundmengen (Variablen) $A,B,\ldots$ ermittelt. Die den Variablen der Grundmengen zugehörigen Terme $a_{i}(A),b_{i}(B),\ldots$ entsprechen vereinfacht den linguistischen Begriffen der Fuzzy-Sets.

Die Zugehörigkeitsgrade wirken auf die mit Expertenwissen erstellten Regeln der Regelbasis und daraus werden unscharfe Stellgrößen und analoge defuzzifizierte scharfe Ausgangssignale gebildet, die statisch auf die Stellorgane eines Prozesses einwirken.

Die Anpassung eines Fuzzy Controllers ohne mathematisches Modell des Prozesses ist mit dem Expertenwissen von einem bekannten Prozess relativ unproblematisch.

Fuzzy-Regler beziehen sich auf die Verfahren der Fuzzy Controller, sind aber meist funktionelle Abwandlungen, Vereinfachungen oder Ergänzungen mit der Fuzzy-Logik.

Der prinzipielle Funktionsmechanismus einer Regelung beruht auf Rückführung der Regelgröße und Eingabe des invertierten Soll-Ist-Wert-Vergleichs in den Regler. Genaue Regelungen mit dem statischen Fuzzy-Controller sind nur in begrenzten Einsatzfällen von nichtlinearen Regelstrecken-Arten möglich.

Optimale Regelungen können durch Erweiterungen des Fuzzy Controllers mit integralen und differenziellen Anteilen der Regelabweichung mit Hilfe empirischer Einstellungen erreicht werden. Sie haben zum Vergleich im Einsatz als Regler an linearen Eingrößen-Regelstrecken keine funktionellen Vorteile gegenüber den klassischen PID-Reglern.

Anwendung der Fuzzy-Controller

Ein Mensch ist in der Lage, mit Hilfe unscharfer Prozess-Informationen über gezielte Eingriffe (Stellgrößen) in den Prozessablauf eine optimale Prozessführung zu gewährleisten. Er kann beispielsweise nach einer Lernprozedur für das Gleichgewicht auf dem Fahrrad durch gezielte Lenkbewegungen geschwindigkeitsabhängige Stell-Fliehkräfte erzeugen, die dank des menschlichen Gleichgewichtssinns das rollende Fahrrad aufrecht halten.

Die auf die Fuzzy-Logik (fuzzy: unscharf, verwischt) basierenden Fuzzy-Controller arbeiten mit Hilfe des Expertenwissens in vergleichbarer Weise. Auch hier werden unscharfe Eingangsgrößen über einen wissensbasierten Regelalgorithmus zu einer definierten Stellgröße verarbeitet.

Fuzzy-Systeme beziehen sich auf sehr spezielle grafische Verfahren mit unscharfen linguistischen Begriffen menschlicher Denkweisen in Verbindung mit einfachen logischen Gleichungen (WENN-DANN-Regelbasis), um aus mehreren Fuzzy-Variablen eine oder mehrere Stellgrößen zu bilden. Zum Verständnis der Wirkungsweise sind Signalflusspläne in Blockschaltbildern erforderlich.

Ein Fuzzy-System kann als ein statisches nichtlineares Übertragungssystem aufgefasst werden. Scharfe Eingangsgrößen führen auch zu scharfen Ausgangsgrößen.

Wesentliche Verfahrensschritte der Konzeption eines Fuzzy-Controllers beziehen sich auf die Fuzzifizierung der linguistischen Variablen zu Zugehörigkeitsgraden, die Zusammenführung der Zugehörigkeiten der linguistischen Terme über die Prämissenauswertung (Min-Max-Operatoren) mit Hilfe der Regelbasis (WENN-DANN-Regeln), der Akkumulation der Stellgrößen und der Defuzzifizierung der Stellgrößen zu einem scharfen analogen Signal (z. B. Flächenschwerpunktmethode). Die Stellgrößen des Fuzzy-Controllers können auf die Stelleinrichtungen einer technischen Anlage wirken, um damit ein gewünschtes technisches Verhalten der Anlage zu erreichen. Ein analoges defuzzifiziertes Stellgrößensignal kann in Verbindung mit einer gegebenen technischen Anlage als Regelstrecke zu einem Regelkreis gestaltet werden.

Für die Anwendung des Fuzzy-Controllers ist das Verständnis der sehr speziellen Fachbegriffe erforderlich.

• Bei Fuzzy-Systemen erfolgt die Quantifizierung von scharfen physikalischen Eingangsgrößen eines Prozesses durch unscharfe Definitionen mit linguistischen Begriffen wie warm, kalt, viel, wenig, mehr, groß, klein.
• Die Fuzzifizierung der scharfen Eingangsgrößen geschieht durch der Gauß’schen Normalverteilung nachempfundene, dreieck- oder trapezförmige sogenannte Fuzzy-Sets in Zugehörigkeiten $\mu$ der entsprechenden Grundmenge, z. B. ein Temperaturbereich $\vartheta$.
• Die verschiedenen Zugehörigkeiten wirken in der Inferenz auf die WENN-DANN-Regeln der Regelbasis. (WENN <Bedingung> DANN <Folgerung>)
• Zur Inferenz (Bedeutung: aufbereitetes Wissen) gehören die Regelbasis, die Implikation und die Akkumulation.
• Die Implikation definiert den Zugriff der Regelbasis auf die Stellaggregate des Prozesses.
• In der nachfolgenden Akkumulation (Anhäufung) wird graphisch die unscharfe Stellgröße (oder mehrere Stellgrößen) abgebildet.
• Die Defuzzifizierung bildet aus der Akkumulation einen scharfen Wert z. B. nach der Flächen-Schwerpunkt-Methode ab, sofern benötigt.

Für das Verhalten einer technischen Anlage z. B. ein lineares oder nichtlineares dynamisches System mit mehreren Ein- und Ausgängen wird kein mathematisch exaktes Modell des Übertragungsverhalten benötigt, sondern ein Expertenwissen zur Abschätzung der linguistischen Variablen. Mit dem Fuzzy-Control-System können sowohl sehr einfache Steuerungen, z. B. Steuerung von Haushaltswaschmaschinen, als auch Regelkreise mit komplexen Industrie-Anlagen gebildet werden.

Fuzzy-Controller werden meist in nichtlinearen Mehrgrößensystemen eingesetzt, die folgende Eigenschaften aufweisen wie:

• Prozesse, deren mathematische Modelle aufwendig oder schwierig zu beschreiben sind.
• Prozesse mit konventionellen Verfahren, die korrigierende Eingriffe von Menschenhand (Anlagenfahrer) erfordern.
• Wenn ein Prozess nur manuell gefahren werden kann.

Das Ziel des Einsatzes der Fuzzy-Controller ist, solche Prozesse zu automatisieren. Anwendungen der Fuzzy-Controller finden sich in allen Bereichen der Industrie bis zu Verbraucherartikeln wie:

• Steuerung von Schienenfahrzeugen oder Regalförderanlagen, bei denen Fahrzeiten, Bremswege und Positionsgenauigkeiten von den Massen, Förderwegen, Schienenhaftwerten und Zeitplänen abhängig sind. Im Allgemeinen handelt es sich bei diesen Prozessen um Mehrgrößensysteme, deren Führungsgrößen Programm-gesteuert und -geregelt werden.

Schema eines inversen Pendels auf einem Wagen

• In der Automobilindustrie wird erfolgreich die Steuerung des Automatik-Getriebes mit der Fuzzy-Logik betrieben.
• Einfachere Anwendungen im privaten Haushalt finden sich in Wasch- und Geschirrspülmaschinen.
• Steuerungen in Fotoapparaten,
• In Hochschulen typisches mechanisches Fuzzy-Demonstrations-Modell einer Regelung eines inversen Pendels mit einem Freiheitsgrad:

Ein fahrbarer Schlitten der Masse M wird durch eine Kraft F horizontal bewegt. Die zu balancierende Pendelmasse m meldet die Pendelstellung durch einen Neigungswinkel θ. Der Neigungswinkel und die Winkelgeschwindigkeit v_θ sind die Eingangs-Messgrößen des Fuzzy-Reglers. Regelgröße ist θ = 90°. Der Regelbereich des Neigungswinkels gilt nur für θ ≫0° und θ ≪ 180° Abweichung vom Stützpunkt des Pendels. Wenn der Standort des Schlittens nicht interessiert, handelt es sich meist um einen Fuzzy-PD-Regler mit 2 Eingangsgrößen und einer Ausgangs-Stellgröße, die auf das mechanische Modell des Pendels als eine instabile nichtlineare Regelstrecke wirkt.

Linguistische Variable und Fuzzy-Mengen

Fuzzy-Mengen

→ Hauptartikel: Fuzzy-Menge

Klassische Definition der Menge

Unter einer Menge $M$ versteht man in der Mathematik eine Zusammenfassung von verschiedenen definierten Objekten. In der klassischen Mengenlehre (scharfe Menge) gehört ein Element $x$ zu einer Menge $M$ (Wahr = Logisch 1) oder nicht zur Menge $M$ (Nicht Wahr = Logisch 0).

Die Funktion $x$ legt die Zugehörigkeit zur Menge $M$ fest, ob Element $x$ in der Menge $M$ enthalten ist.

$x(M)={\begin{cases}1,&{\text{wenn }}x\in M\\0,&{\text{wenn }}x\notin M\end{cases}}$

Man unterscheidet:

Aufzählende Schreibweise: M = {Element 1, Element 2, …}

Beschreibende Mengenschreibweise: M = {x | x besitzt die Eigenschaften E 1 , E 2 , …, E n}

Definition der Fuzzy-Menge

Begriff-Definitionen:

• Unter Fuzzifizierung versteht man die Umwandlung einer scharf definierten Eingangsgröße innerhalb der Dimension einer Grundmenge in einen oder mehrere Zugehörigkeitswerte.
• Eine linguistische Variable $A$ repräsentiert meist eine physikalische Größe in einem beliebigen System als Grundmenge. Diese Variable ist durch linguistische Terme (Fuzzy-Sets) $a(A)$ definiert.
• Umgangssprachlich sind zu Ereignissen oder Vorgängen Begriffe der linguistischen Variablen üblich, welche keine eindeutigen Zugehörigkeiten zu einer Menge erlauben, wie warm, groß, dick, nah, kurz, alt usw. Diese Begriffe von Teilmengen können durch die Fuzzy-Sets z. B. in einem technischen Prozess definiert werden, wenn Expertenwissen vorliegt.
• Linguistische Terme (Fuzzy-Sets) sind unscharfe Teilmengen $a(A)$ der Grundmenge $A$. Bezieht sich die Grundmenge $A$ z. B. auf die Wärme in der Dimension der Temperatur, dann sind die linguistischen Begriffe der Teilmengen (Fuzzy-Sets): [kalt, warm, heiß, sehr heiß] oder symbolisch $a_{1},a_{2},a_{3}\ldots$, die mittels Expertenwissen als Fuzzy-Sets in ein Koordinatensystem übertragen werden.
• Die Fuzzy-Sets sind als linguistische Terme $a_{1}\ldots a_{n}$ in Form von grafischen Symbolen meist als Dreiecke und Trapeze auf der Abszisse eingezeichnet. Siehe Diagramm im nächsten Abschnitt.
• Die linguistische Variable $A$ ist auf der Abszisse eines Koordinatensystems eingetragen und enthält die Dimension einer meist physikalischen Größe. Ein skalierter Wert aus der linguistische Variablen (Grundmenge) $A$ entspricht einer Eingangsgröße $e(A)$ zur Fuzzifizierung der Teilmenge (Fuzzy-Set) in einen Zugehörigkeitsgrad $\mu$.
• Die Zugehörigkeitsfunktion (= Membership = Mitgliedschaft) definiert für ein scharfes Ausgangssignal für $0<\mu (A)<1$ die Zugehörigkeit der Variablen $A$ (Grundmenge) auf einen der Terme $a_{1}\ldots a_{n}$ (Teilmengen) den entsprechenden Zugehörigkeitsgrad $\mu$ zwischen 0 und 1 (= 0 und 100 %) z. B. $0{,}3:=30\,\%$.
• Der Zugehörigkeitsgrad $\mu \,(A)=\mu _{a1}\ldots \mu _{an}$ ist die fuzzifizierte scharfe Ausgangsgröße, wenn die scharfe Eingangsgröße $e(A)$ einem Wert der Grundmenge (der Abszisse) entspricht. Bei überlappenden Fuzzy-Sets können durch ein Signal der Eingangsgröße $e(A)$ auch mehrere Fuzzy-Sets getroffen werden. Z. B. $\mu _{a2}=0{,}2,\ \mu _{a3}=0{,}5$. Verschiedene Werte des Eingangssignals $e(A)$ können auch gleiche Werte des Zugehörigkeitsgrades $\mu$ hervorrufen.
• Expertenwissen beruht auf Erfahrungen eines Experten, der das Verhalten eines linearen oder nichtlinearen beliebigen technischen Systems beurteilen kann und linguistische Variablen als Grundmengen festlegen kann.
• Linguistische Variablen werden üblich mit großen Anfangsbuchstaben A, B, C, … bezeichnet. Die Ausgangsgrößen eines Fuzzy-Controllers bezeichnet man mit den Endbuchstaben des Alphabetes X, Y, Z.

Die scharfe Trennung der klassischen Mengen mit der Beurteilung (wahr oder nicht wahr) wird in der Theorie der Fuzzy-Mengen aufgehoben und durch sogenannte Fuzzy-Sets als unscharfe Teilmengen ersetzt. Fuzzifizierte Mengen stellen zwischen einem Wert der Grundmenge $A$ und den Elementen (Teilmengen mit den Symbolen der Fuzzy-Sets) $a_{1}\ldots a_{n}$ einer Grundmenge eine meist lineare Beziehung zu einer Ausgangsgröße – dem Zugehörigkeitsgrad $\mu$ – her.

Eine Fuzzy-Menge wird also durch eine graphische Methode über ein Koordinatensystem bestimmt, in dem sogenannte Fuzzy-Sets als grafische Elemente wie Dreiecke, Trapeze eingezeichnet sind. Fuzzy-Sets erlauben auch die Beschreibung nichtlinearer Zusammenhänge zwischen Ein- und Ausgangsgrößen eines Systems (z. B. technische Anlage) mit Hilfe von linguistischen unscharfen Begriffen wie [sehr wenig, wenig, mehr, viel, …], die durch Expertenwissen festgelegt werden.

Fuzzy-Teilmengen (linguistische Terme) sind – der grafischen Darstellung der Gaußschen Glockenkurve zur einfacheren Berechenbarkeit nachempfundene – meist dreieckförmige oder trapezförmige Funktionen. Sie sind Bestandteil einer Grundmenge $A$ (Linguistische Variable) und werden als grafische Modelle je nach Anzahl der linguistischen Terme in einem Koordinatensystem dargestellt. Die Abszisse enthält die skalierte physikalische Dimension der Grundmenge (linguistische Variable), innerhalb der die Terme als Fuzzy-Sets mit ihren Stützpunkten meist überlappend aufgeteilt sind. Die Ordinate kennzeichnet sämtliche Teilmengen (Fuzzy-Sets) durch den Zugehörigkeitsgrad $\mu (A)$.

Je nachdem wie viele Fuzzy-Sets eine Grundmenge $A$ enthält, so oft kann abhängig von einem Eingangswert $e(A)$ der Grundmenge der Zugehörigkeitsgrad $\mu (A)$ = 0 bis 1 erreicht werden. Es hängt also von dem Wert $e(A)$ innerhalb der Grundmenge $A$ ab, welcher Fuzzy-Set und wie viele Fuzzy-Sets aktiviert („feuern“) werden und welche Zugehörigkeitsgrade $\mu (A)$ sich daraus ergeben.

Trifft eine Eingangsgröße mit einem Wert der Grundmenge auf ein überlappendes Fuzzy-Set, können sich mehrere Werte des Zugehörigkeitgrades $\mu \,(A)=\mu _{a1}\ldots \mu _{an}$ auf der Ordinate ergeben. Verschiedene Werte des Eingangssignals $e(A)$ können gleiche Werte des Zugehörigkeitsgrades $\mu$ hervorrufen.

Es existieren verschiedene Begriffe der Funktionen der unscharfen Teilmengen, die alle das Gleiche bedeuten: Fuzzy-Set, Fuzzy-Element, Term einer Fuzzy-Variablen, linguistischer Term.

Linguistische Variablen des Fuzzy-Controllers

Eine Fuzzy-Variable bezieht sich auf die Grundmenge einer skalierten physikalischen Größe, deren Terme Fuzzy-Sets darstellen und grafisch in einem Koordinatensystem – wie bereits erläutert – abgebildet ist.

Ein grafisches Modell der Signalflüsse des Fuzzy-Controllers besteht aus mehreren Eingangs- und Ausgangsvariablen, die durch mehrere Arbeitsregeln der Regelbasis miteinander verknüpft sind. Die scharfen Eingangssignale dieses Modells werden fuzzifiziert und die verarbeiteten unscharfen Ausgangssignale werden zu Stellgrößen defuzzifiziert.

Fuzzy-Variablen sind meist physikalische Größen, wie z. B. die „Temperatur“, deren linguistische Terme als Fuzzy-Sets wie „sehr kalt“, „kalt“, „warm“, „sehr warm“ definiert werden können. Andere Fuzzy-Variablen wie z. B. die „Entfernung“ können durch die linguistischen Terme wie „sehr nah“, „nah“, „weit“, „sehr weit“ beschrieben werden. Ein linguistischer Term wird als eine Fuzzy-Teilmenge über eine Grundmenge definiert.

Häufig werden auch Abkürzungen von Standardbegriffen für beliebige physikalische Größen verwendet wie „positiv groß“, „positiv mittel“, „positiv klein“, „nahe null“, „negativ groß“, „negativ mittel“, negativ klein. Dies sind bereits 7 Terme, die sich bei einem Eingrößensystem auf eine Eingangs-Ausgangs-Kennlinie beziehen, die durch den Ursprung des Koordinatensystems vom positiven bis in den negativen Bereich geht. Handelt es sich bei dem Prozess um Mehrgrößensysteme, ist die Eingangs-Ausgangs-Beziehung des Fuzzy-Controllers durch Kennfelder bestimmt.

Zwischen den zwei linguistischen Begriffen einer Grundmenge der Temperatur wie „warm“ und „sehr warm“ hat diese Eigenschaft je einen Wahrheitsgrad der Zugehörigkeit zwischen 0 und 1. Diese Terme der variablen Temperatur entsprechen den menschlichen Empfindungen. Dennoch besteht eine gewisse Willkür in der Festlegung und Zuordnung der Fuzzy-Sets mit ihren Stützpunkten über der Grundmenge der Variable „Temperatur“. Hier spielt bereits das Expertenwissen eine Rolle, denn es besteht in dem linguistischen Begriff Wärme bekanntermaßen ein Unterschied, ob es sich bei dem Term „sehr warm“ um die Badewasser-Temperatur oder die Tee-Wasser-Temperatur handelt.

Darstellung einer Fuzzy-Grundmenge A mit 6 Teilmengen a1 … a6

Dreieckige und trapezförmige Fuzzy-Sets sind wegen der einfachen Berechenbarkeit die am häufigsten verwendeten Formen einer unscharfen Teilmenge von Fuzzy-Variablen.

Singletons (Strichfunktionen) entsprechen scharfen linguistischen Elementen (Termen), die nur je einen physikalischen Wert repräsentieren und werden meist zur Vereinfachung bei der Defuzzifizierung eingesetzt. Ist x₀ ein bestimmter Wert der Grundmenge X, dann ist nur an der Stelle x = x₀ für den Zugehörigkeitsgrad ein von null verschiedener Wert gegeben. Für die Schlussfolgerung des DANN-Teils einer WENN-DANN-Regel können zur Vereinfachung der rechnerischen Auswertung Singletons anstelle dreieckförmiger oder trapezförmiger Fuzzy-Sets eingesetzt werden. Details folgen im Kapitel Inferenz.

Für die Beschreibung eines technischen Vorgangs einer physikalischen Signalgröße sind häufig eine Anzahl von 2 bis 7 Fuzzy-Sets einer Grundmenge ausreichend.

Fuzzy-Sets werden zum besseren Verständnis grafisch in einem Koordinatensystem auf einer Abszisse mit scharfen Werten der physikalischen Größe eingeordnet und für beliebige Grundmengen in der Ordinate dem Zugehörigkeitsgrad μ = 1 ≡ 100 % zugeordnet. Die Trapez- oder Dreiecksformen der Fuzzy-Sets sind häufig – aber nicht immer – symmetrisch gestaltet und überschneiden sich innerhalb eines bestimmten Bereiches in den Fußpunkten meist zwischen 20 und 50 % auf der Abszisse. Falls keine Überschneidung vorliegt, hat in Eingrößensystemen die Ausgangsgröße in diesem bestimmten Bereich den Zugehörigkeitsgrad null und ebenso die Eingangs-Ausgangs-Kennlinie.

Durch die Wahl der Lage der Fuzzy-Sets – die Größe der Überschneidung (Überlappung), der Symmetrie der Sets, der Art der Regelbasis – kann bei Eingrößensystemen die Eingangs-Ausgangskennlinie des Fuzzy-Reglers in weiten Grenzen von linear bis kontinuierlich nichtlinear und gebrochen nichtlinear gestaltet werden.

Die Anzahl der Variablen und der zugehörigen Terme soll so gering wie möglich sein, weil sie insbesondere bei der Berechnung der Erfüllungsgrade und Verknüpfungen von Variablen mit den Fuzzy-Regeln viel Rechenarbeit an einem Microrechner bedeuten.

Definition indizierter Fuzzy-Variablen und deren Symbole

Beschränkt man sich auf die Darstellungen der Fuzzy-Variablen und gängigsten Fuzzy-Operatoren, handelt es sich bei der Fuzzy-Logik um ein recht einfaches Verfahren, Steuerungstechnik und mit Einschränkungen Regelungstechnik ohne genaue Kenntnisse eines dynamischen Mehrgrößen-Prozesses als Regelstrecke mit Erfolg anzuwenden. Dies ist größtenteils in den dargestellten grafischen Funktionsdiagrammen erkennbar. Dagegen ist die mathematische Beschreibung der signaltechnischen Funktionen der scharfen Eingangssignale bis zu den scharfen Signal-Ausgangsgrößen (Stellgrößen) des Fuzzy-Controllers schwierig.

Die Fachliteratur zeigt keine einheitliche Benennung von Fuzzy-Variablen, Teilmengen, Grundmengen, sowie Variablen-Symbolen und deren Indizierungen. Insbesondere Veröffentlichungen aus dem universitären Bereich können wenig geübten Interessenten bei mehrfachen Indizierungen von Erfüllungsgraden, unscharfer Mengen und Regeln Verständnis-Schwierigkeiten der Fuzzy-Theorie bereiten.

Zum leichteren Verständnis wird folgende Vereinfachung der Benennung von Variablen und deren Indizierungen definiert:

• Scharfe regelungstechnische Ein- und Ausgangssignale

Scharfe Ein- und Ausgangssignale werden entsprechend der allgemein eingeführten Symbole der Regelungstechnik mit e1, e2…e_n für die Eingangssignale und u1, u2…u_n für die Ausgangssignale bezeichnet. Die Indizierung n bedeutet eine endliche ganze Zahl von 1…≪ ∞.

• Unscharfe Signale

Ein fuzzifiziertes Signal entspricht einer Funktion des Zugehörigkeitgrades μ = f [e, Fuzzy-Variable, Fuzzy-Term (Fuzzy-Set)] einer als Folge eines scharfen Eingangssignals e getroffenen Fuzzy-Teilmenge (Fuzzy-Set) der Fuzzy-Variablen mit der Grundmenge, die dem Bereich der Eingangssignal-Werte e zugeordnet ist. Zur Kennzeichnung der Zugehörigkeit wird μ mit dem linguistischen Begriff der Teilmenge bzw. mit einem zugehörigen Buchstaben-Symbol indiziert.

Unscharfe Signale ergeben sich aus der fuzzy-logischen Bearbeitungsprozedur aller Signalwerte der Inferenz nach der Fuzzifizierung und vor der Defuzzifizierung. Während die linguistische Variable einer Grundmenge einen Signal-Kanal darstellt, bedeutet für ein gegebenes scharfes Eingangssignal der aktivierte zugehörige linguistische Term (Fuzzy-Set) bzw. der Zugehörigkeitsgrad dieses Terms bereits den unscharfen Signalwert.

• Fuzzy-Variablen

Die Fuzzy-Variablen für Ein- und Mehrgrößensysteme beziehen sich auf skalierte Grundmengen und enthalten eine begrenzte Anzahl von Zugehörigkeitsfunktionen (= Terme, = Elemente, = Fuzzy-Sets). Fuzzy-Variable werden mit Großbuchstaben des Anfangs-Alphabetes A, B, C…. bezeichnet. Die Fuzzy-Ausgangsvariablen können mit den Großbuchstaben des End-Alphabetes z. B. X, Y, Z oder bei einer Ausgangsgröße mit U als regelungstechnische Stellgröße bezeichnet werden.

Fuzzy-Eingangsvariable dienen der Umsetzung scharfer Eingangssignale in unscharfe Teilmengen (Fuzzy-Sets). Sie sind Bestandteil der Prämisse (WENN-Teil einer Arbeitsregel).

Fuzzy-Ausgangsvariable dienen der Umsetzung unscharfer Teil-Stellgrößen nach der Akkumulation (Zusammenfassung) in scharfe Stellgrößen. Sie sind Bestandteil der Konklusion (DANN-Teil einer Arbeitsregel).

• Fuzzy-Terme (Fuzzy-Sets) als Teilmengen der Fuzzy-Variablen

Die erforderliche Indizierung von Fuzzy-Variablen mit den langen linguistischen Begriffen der Fuzzy-Terme ist in Gleichungen ungeeignet. Stattdessen werden die Symbole der Variablen A in gleicher Reihenfolge mit a1, a2, …, a_n, bei Variablen B mit b1, b2, …, b_n bezeichnet. Dies gilt sinngemäß für weitere Variablensymbole!

• Zugehörigkeit μ der Fuzzy-Eingangsgrößen

Der Zugehörigkeitsgrad μ(A) oder μ(B) mit dem Maximalwert 1 über einer Variable der Grundmengen A, B, … bezieht sich immer auf einen Term (Fuzzy-Set) einer Variablen eines grafischen Fuzzy-Modells. Das grafische Modell stellt die Beziehung der Zugehörigkeit auf der Ordinate zur Grundmenge auf der Abszisse im Koordinatensystem dar. Die Grundmenge entspricht der Dimension der physikalischen Eingangsgröße. Beispielsweise gilt das Symbol ϑ für die Skalierung der Temperatur der Grundmenge der Variablen A auf der Abszisse.
μ_a1(ϑ) = 1 entspricht dem maximalen Zugehörigkeitsgrad eines Fuzzy-Sets (Teilmenge) a1 der Variable A in der Dimension der Temperatur.

• Zugehörigkeit μ als Ausgangsgröße (Verfahren Mamdani)

Das grafische Fuzzy-Modell der unscharfen Ausgangsgrößen entspricht dem der unscharfen Eingangsgrößen. Die Zugehörigkeit μ einer Fuzzy-Ausgangsvariable wird als Schlussfolgerung aus dem Prämissen-Ergebnis der Eingangsgröße ermittelt. Dazu ist die Kenntnis der zu verwendenden Fuzzy-Regeln und der Fuzzy-Operatoren erforderlich.

Für den Fall, dass eine unscharfe Teil-Stellgröße (Fuzzy-Set) der Variable U (Grundmenge) als Fuzzy-Set u3 = „Ventil 2/3 auf“ lautet, dann bedeutet der Zugehörigkeitsgrad μ_u3(U) = 0,5, dass die Fuzzy-Teilmenge bei Verwendung von min- oder max-Operatoren der Prämissenauswertung eine trapezförmige Form der Höhe 0,5 hat.

• Erfüllungsgrad und Zugehörigkeitsfunktion einer Fuzzy-Teilmenge

Während sich die Zugehörigkeitsfunktion a1(ϑ) als eine Funktion eines Fuzzy-Sets darstellt, ist der Zugehörigkeitsgrad ein bestimmter Wert der Zugehörigkeit z. B. μ_a1(A) = 0,5, der sich aus einem scharfen Wert der Grundmenge A nach einer zugehörigen Arbeitsregel der Regelbasis für einen bestimmten Term a1 ergibt.

Dieser Wert des Zugehörigkeitsgrades für einen bestimmten aktivierten Fuzzy-Set z. B. μ_αi(A) = 0,5 wird auch mit „Erfüllungsgrad der Prämisse“ (Wenn-Teil der Regel) bzw. „Erfüllungsgrad der Regel“ bezeichnet. In der Fachliteratur wird dieser Begriff des Erfüllungsgrades auch vereinfacht mit α (Alpha-Schnitt, Alpha oder H = Trapezhöhe) bezeichnet. α oder H ist aber immer ein Wert, der sich auf die Zugehörigkeit μ bzw. auf die Ordinate des grafischen Fuzzy-Modells bezieht.

Berechnung der Fuzzy-Sets mit Geradengleichungen

Gebräuchliche Fuzzy-Sets als Fuzzy-Teilmengen einer Fuzzy-Variablen

Das grafische Modell einer Fuzzy-Variablen entspricht mittels Expertenwissen einer Aufteilung von normalerweise überlappenden Fuzzy-Sets auf die Grundmenge X auf der Abszisse im Koordinatensystem. Die maximale Höhe aller Fuzzy-Sets der Variable X entspricht dem Erfüllungsgrad μ(X) = 1 der Ordinate. Für die Fuzzifizierung einer scharfen Eingangsgröße e im Bereich der Grundmenge der Variablen X lässt sich grafisch leicht der Zugehörigkeitsgrad oder die Zugehörigkeitsgrade der Fuzzy-Sets mit einer bestimmten Genauigkeit darstellen. Da es sich bei dem Fuzzy-Controller um einen Mikrocomputer handelt, der mathematische und logische Operationen durchführen kann, müssen für die Berechnungen der Erfüllungsgrade an dreieckförmigen oder trapezförmigen Fuzzy-Sets Geradengleichungen verwendet werden.

Es hängt also von der Größe des scharfen Eingangssignals innerhalb der Grundmenge ab, welches Fuzzy-Set und ob es die ansteigende Rampe oder abfallende Rampe trifft und ob bei überlappenden Fuzzy-Sets zwei Fuzzy-Sets getroffen werden.

Bei den in der Grafik dargestellten Fuzzy-Set-Modellen mit den Bezeichnungen der Eckwerte a, b, c, d und dem Erfüllungsgrad μ(X)= 1 entspricht die Größe x der Eingangsgröße e. Der Erfüllungsgrad μ(X)= 1 wird abhängig von der Größe des Eingangssignals im Bereich der Grundmenge sooft getroffen, soviel Terme einer Variable zugeordnet wurden.

Für eine Fuzzy-Variable mit mehreren Fuzzy-Sets muss für die Bestimmung des Erfüllungsgrades abhängig von der scharfen Eingangsgröße und der Lage der Rampe die Geradengleichungen des Anstiegs und des Abfalls berechnet werden. Daraus erfolgt bei der Verknüpfung der Erfüllungsgrade mit weiteren Variablen die Ermittlung der unscharfen Ausgangsvariablen (Fuzzy-Teilstellgrößen).

Für die Berechnung der Zugehörigkeitsfunktion μ(X) für einen gegebenen scharfen Wert der der Eingangsgröße e auf der skalierten Abszisse einer Grundmenge sind folgende Geradengleichungen der Rampen gegeben:

Geradengleichung für den Anstieg der Rampe:

$\mu (x,a,b,c)={\frac {x-a}{b-a}}\qquad {\text{für}}\ a\leq x\leq b$

Geradengleichung für den Abfall der Rampe:

$\mu (x,a,c,d)={\frac {d-x}{d-c}}\qquad {\text{für}}\ c\leq x\leq d$

Fuzzy-Operatoren

Operationen mit unscharfen Mengen sind notwendig, wenn mehrere linguistische Aussagen der WENN-DANN-Regeln verknüpft werden müssen. Neben unscharfen Mengen sind unscharfe Relationen ein wichtiges Teilgebiet der Fuzzy-Set-Theorie. Die Beziehungen gleicher Grundmengen benachbarter Fuzzy-Sets werden durch Fuzzy-Relationen über die gängigsten Operatoren wie Fuzzy-ODER, Fuzzy-UND und Fuzzy-NICHT-Funktionen beschrieben. Diese Beziehungen haben eine andere Bedeutung, als die der Bool´schen Algebra, denn sie müssen auch einen Bezug zu den unscharfen Mengen besitzen. Die Unterteilung des Wahrheitsgehaltes in beliebig viele Zwischenschritte zwischen wahr und falsch kommt der menschlichen Denkweise näher, als die zweiwertige Logik.

UND-ODER-NICHT-Operatoren zur Verknüpfung von Zugehörigkeitsfunktionen (Teilmengen)

Das Verhalten eines Fuzzy-Controllers ist durch sogenannte Arbeitsregeln der Regelbasis bestimmt, die aus einem WENN-Teil und einem DANN-Teil bestehen. Die Verknüpfung der Fuzzy-Teilmengen gleicher oder ungleicher Grundmengen erfolgt mittels der Fuzzy-Operatoren. Die 3 am häufigsten genutzten Operatoren zur Verknüpfung von fuzzifizierten Teilmengen lauten wie folgt:

• UND-Operator

Der MIN-Operator bildet den Mengendurchschnitt von Fuzzy-Sets. Die UND-Verknüpfung entspricht dem Durchschnitt der beiden Flächen der Fuzzy-Sets.

Beispiel der Verknüpfungsmengen μ_x1 und μ_x2 der Grundmenge X:

$\mu _{x}(X)=\min[\mu _{x1}(X),\mu _{x2}(X)]=[\mu _{x1}\cap \mu _{x2}](X)$

Beispiel Min-Operator für μ_x1 = 0,2 und μ_x2 = 0,4:

$\mu _{\min }(X)=\min[0{,}2(X);0{,}4(X)]=0{,}2(X)$

Weitere UND-Operatoren, die weniger genutzt werden:

prod-Operator (algebraisches Produkt) und min-avr-Operator (kombiniert den min-Operator mit dem arithmetischen Mittel)

• Der ODER-Operator

Die ODER-Verknüpfung zweier Fuzzy-Mengen stellt sich als Vereinigung mit dem Maximum-Operator dar. Der max-Operator bildet die Mengenvereinigung der Fuzzy-Sets.

Beispiel der Verknüpfungsmengen μ_x1 und μ_x2 der Grundmenge X:

$\mu _{x}(X)=\max[\mu _{x1}(X),\mu _{x2}(X)]=[\mu _{x1}\cup \mu _{x2}](X)$

Beispiel Max-Operator für μ_x1 = 0,2 und μ_x2 = 0,4:

$\mu _{\max }(X)=\max[0{,}2(X);0{,}4(X)]=0{,}4(X)$

Weitere ODER-Operatoren, die weniger genutzt werden:

probor-Operator (probabilistisches ODER algebraische Summe) und max-avr-Operator (kombiniert den max-Operator mit dem arithmetischen Mittel)

• NICHT-Funktion

Der Komplement-Operator bildet das Komplement μ_x des Fuzzy-Sets μ_x1 der Grundmenge X mit folgender Operation:

$\mu _{x}(X)=1-\mu _{x1}(X)$

Fuzzy-Relationen

Relationen eignen sich zur Beschreibung von Zusammenhängen zwischen verschiedenen Variablen und Attributen. Eine Fuzzy-Relation entspricht einer Fuzzy-Menge, deren Grundmenge ein kartesisches Produkt aus mehreren Grundmengen darstellt. Mehrstellige Relationen sind Beziehungen zwischen scharfen oder unscharfen Mengen auf unterschiedlichen Grundmengen. Eine mehrstellige Relation ist eine Teilmenge der kartesischen Produktmenge der Grundmengen, eine unscharfe Relation ist immer eine unscharfe Menge.

Während eine gewöhnliche Relation als Teilmenge von $A\times B$ durch die zugehörige Indikatorfunktion $A\times B\longrightarrow \{0,1\}$ charakterisiert ist, ist eine zweistellige Fuzzy-Relation (unscharfe Relation) eine Abbildung von $A\times B$ in das Einheitsintervall

$A\times B\longrightarrow [0,1]\;.$

Die nebenstehende Grafik „Regelaktivierung mit ungleichen Grundmengen“ zeigt als Relationsvorschrift R die Relation der Zugehörigkeitsgrade nach der Regel 1:

Regelaktivierung mit zwei Fuzzy-Teilmengen (Fuzzy-Sets) als Folge von 2 scharfen Eingangsgrößen e1 und e2

Die Terme a_n und b_n dieser Variablen A und B geben an, wie stark sie zueinander in Relation stehen. In einer Relations-Matrix z. B. mit den Variablen A, die einer Grundmenge der Temperatur entspricht und der Variablen B, die einer Grundmenge des Drucks entspricht, lässt sich folgende Relation der Terme a2 = „warm“ und b2 = „Druck mittel“ bilden, deren Zuordnung für eine bestimmte Arbeitsregel der Regelbasis gültig ist.

$\underbrace {{\text{WENN Temperatur ist warm}}\quad UND\quad {\text{Druck ist mittel}}} _{\text{WENN A = a2 UND B = b2 }}\quad \underbrace {DANN\quad {\text{Ventil ist 2/3 auf}}} _{\text{DANN U = u3}}$

Die Teilmengen der Terme „warm“ und „mittel“ werden als Relation der Grundmengen Temperatur und Druck dargestellt. Zur Bestimmung der Zugehörigkeiten μ_R der UND-Verknüpfung der Prämissen des WENN-Teils kommt der min-Operator zur Anwendung.

$\mu _{R}(A,B)=\min\{\mu _{ai}(A),\mu _{bi}(B)\}$

Zahlenbeispiel der Fuzzy-Relation (Prämissenrelation von 2 Fuzzy-Sets ungleicher Grundmengen):

Für einige wenige in gleichen Abständen (Äquidistanz: = „gleiche Abstände auf einer Skala“) mit 5 aktiven Messpunkten gewählte scharfen Eingangssignale e1 und e2 für die Zugehörigkeitsgrade μ = {0; 0,5; 1,0; 0,5; 0} werden die Teilmengen (Fuzzy-Sets) a2(A) und b2(B) aktiviert. Für die angegebenen Zugehörigkeitsgrade lassen sich laut der nebenstehenden Grafik mit der einfachen Skalierung die zugehörigen scharfen Werte der Eingangssignale für die Temperatur und den Druck ermitteln. Laut der nachstehenden Tabelle ist jeder Wert des Terms a2 mit jedem Wert des Terms b2 für eine bestimmte Zugehörigkeit zugeordnet. Es handelt sich hierbei um die Prämissenauswertung des WENN-Teils der zugehörigen Arbeitsregel.

Die skalierten Daten der Grundmenge der Temperatur von Variable A lauten: {20; 40; 60; 80; 100}(ϑ)

Die skalierten Daten der Grundmenge des Druckes von Variable B lauten: {4; 8; 12; 16; 20}(P)

Die UND-Verknüpfung der Terme erfolgt über den Min-Operator nach Regel 1 laut dargestellter Grafik der Fuzzy-Variablen.

Das Ergebnis der Tabelle sind die regelaktivierten Zugehörigkeitswerte μ_R von zwei unscharfen Teilmengen a2 und b2, die über einige Werte der beiden skalierten Grundmengen gefunden wurden.

Tabellarische Darstellung der Zugehörigkeitsgrade (Erfüllungsgrade) als Fuzzy-Relationen der Grundmengen Temperatur und Druck mit den Teilmengen „Temperatur warm“ und „Druck mittel“ laut obengenannter Arbeitsregel:

	Variable Druck, Term „mittel“
Variable Temp. Term „warm“	4 bar	8 bar	12 bar	16 bar	20 bar
20 °C	0	0	0	0	0
40 °C	0	0,5	0,5	0,5	0
60 °C	0	0,5	1,0	0,5	0
80 °C	0	0,5	0,5	0,5	0
100 °C	0	0	0	0	0

Die praktische Bedeutung dieser Tabelle bezieht sich auf die Bestimmung der Zugehörigkeitsgrade der Schlussfolgerung der Arbeitsregel. Zur Realisierung eines Rechenprogrammes für einen Fuzzy-Controller müssen die Zugehörigkeitsgrade eines jeden Fuzzy-Set mit den diskreten Werten der Grundmengen über Geradengleichungen bestimmt werden. Für die logischen Verknüpfungen der Teilmengen eignen sich die Min-max-Operatoren. Aus der Zusammenfassung der Schlussfolgerung des DANN-Teils einer jeden Regel wird die Funktion der Fuzzy-Teil-Stellgröße und mit der Akkumulation die Fuzzy-Stellgröße ermittelt.

Übersichtsdarstellung des Fuzzy-Controllers

Prinzip des Fuzzy-Controllers

Das Konzept des Fuzzy-Controllers nach Mamdani bezieht sich auf folgende Teilfunktionen:

Die Wissensbasis enthält das gesamte Expertenwissen, das sich anhand von Erfahrungen mit linguistischen Begriffen und Handlungen auf die Steuerung eines nichtlinearen Prozesses bezieht. Mit ihrem Wissen wird die Voraussetzung geschaffen, die scharfen System-Eingangssignale in Fuzzy-Sets umzusetzen und die Fuzzy-Regeln der Regelbasis zu formulieren.

Elemente (Terme, Fuzzy-Sets) von unscharfen Mengen werden durch ein Wertepaar beschrieben, welches aus dem scharfen Wert der Grundmenge z. B. der Variable A und dem Zugehörigkeitsgrad μa(A) besteht. Der scharfe Wert der Grundmenge der Variable A kann ein Wert eines Eingangssignals e sein.

Die Regelbasis enthält die fuzzy-logischen Steuerregeln zur Bestimmung der unscharfen Ausgangsvariablen (unscharfen Stellgrößen) aus den unscharfen Eingangsvariablen.

Datenherkunft für den Entwurf des Fuzzy-Controllers:

• Befragung oder Beobachtung der Experten bei der ihrer Prozessbedienung,
• Analyse des Prozesses und Erstellung einfacher Prozessmodelle,
• Ableitung von Daten aus dem vereinfachten Prozessmodell.

Projektierungstrategie:

• Modell der Grundmengen der Ein- und Ausgänge des Fuzzy-Controllers festlegen.
• Zugehörigkeitsfunktionen (Fuzzy-Sets) innerhalb der Grundmenge anordnen.
• Steuerregeln als Regelbasis aufstellen.

Beispiel einer linguistischen Steuerregel eines Fuzzy-Controllers mit zwei Eingangsgrößen und einer Ausgangsgröße:

${\text{Regel}}\colon \ \ \underbrace {WENN\ \ \underbrace {{\text{Innentemp kühl}}\ \ UND\ \ {\text{Außentemp kalt}}} _{Pr{\ddot {a}}missen\ (Vorbedingung)}\ \ DANN\ \ \underbrace {\text{Heizung auf Maximum}} _{Konklusion\ (Schlussfolg.)}} _{Implikation\ (Fuzzy-Regel)}$

Kurzfassung der Funktionen des Fuzzy-Controllers:

Grafisches Fuzzy-Modell einer Fuzzy-Variablen Jede Fuzzy-Variable wird als grafisches Modell dargestellt, in dem die sogenannte Grundmenge als eine skalierte physikalische Signalgröße (z. B. ein Temperaturbereich) auf der Abszisse in einem Koordinatensystem aufgetragen ist. Innerhalb des Bereiches der Grundmenge werden die meist dreieckförmigen Fuzzy-Teilmengen (Fuzzy-Sets) mit ihren Stützpunkten auf der Abszisse nach Expertenwissen meist überlappend aufgeteilt. Der Ordinate ist der Zugehörigkeitsgrad der einzelnen Fuzzy-Sets mit dem Maximalwert μ = 1 ≡ 100 % zugeordnet. Fuzzifizierung Scharfe sich ändernde Eingangssignale treffen je nach Größe im Bereich der Grundmenge verschiedene Fuzzy-Sets und ergeben wechselnde kontinuierlich steigende oder fallende Zugehörigkeitsgrade zwischen 0 und 1. Die Zugehörigkeitsgrade innerhalb des Bereiches eines Fuzzy-Sets können als fuzzifizierte Signale aufgefasst werden. Bei überlappenden Fuzzy-Sets werden je nach Größe eines gegebenen Wertes des Eingangssignals e ein oder zwei benachbarte Fuzzy-Sets aktiviert. Damit ergeben sich z. B. für eine Variable A zwei Zugehörigkeitsgrade μa1(A) und μa2(A). Das Ergebnis der Abbildung eines scharfen Wertes der Eingangsgröße e zu den Zugehörigkeitsfunktionen (Fuzzy-Sets) einer Fuzzy-Variable bezeichnet man auch als Vektor der Zugehörigkeitsfunktionen. Beispiel: Fuzzy-Variable A, Fuzzy-Sets a1...a5, Fuzzy-Sets a3 und a4 aktiv. $e\ {\xrightarrow {\text{fuzzifiziert}}}\ \mu _{a}=\{0\ \ 0\ \ 0{,}8\ \ 0{,}3\ \ 0\}$ Inferenz: Für jeden scharfen Wert eines Eingangssignals einer Variable wird der gewonnene Zugehörigkeitsgrad μ des zugehörigen Fuzzy-Sets mit sogenannten WENN-DANN-Regeln der Regelbasis auf den Wahrheitsgehalt überprüft und gegebenenfalls erfolgt im DANN-Teil der Regel eine Zuweisung an die Ausgangs-Variable als unscharfe Teil-Stellgröße. Ist im WENN-Teil eine „Vorbedingung“ laut Regel erfüllt (Prämissen-Auswertung), d. h. ein Fuzzy-Set ist für ein scharfes Eingangssignal aktiv, dann erfolgt im DANN-Teil die Schlussfolgerung (Konklusion) als eine Zuweisung auf eine Ausgangsvariable. Nach der „Mamdani-Implikation“ darf der Wahrheitsgehalt der Konklusion nicht größer sein, als der Wahrheitsgehalt der Prämisse. Die Zugehörigkeitsgrade von mehreren scharfen Signaleingängen über Fuzzy-Variablen mit unterschiedlichen Grundmengen werden mit min-max-Operatoren verknüpft. Danach erfolgt die Zuweisung auf eine Fuzzy-Ausgangsvariable oder mehrere Ausgangsvariablen als unscharfe Teil-Stellgrößen. Die Teilstellgrößen einer Ausgangsvariable werden zu einer unscharfen Stellgröße akkumuliert. Defuzzifizierung: Aus der akkumulierten unscharfen Stellgröße wird die scharfe Stellgröße nach verschiedenen Verfahren errechnet.

Aufbau des Fuzzy-Controllers

Begriffsklärung

In der deutschen Fachliteratur haben sich eine Reihe von Fremdbegriffen für die Beschreibung der Fuzzy-Controller etabliert, die nicht alle einheitlich verwendet werden.

Die wichtigsten Begriffe:

Regelbasis Die Regelbasis ist eine Aufstellung von Regeln nach linguistischen Begriffen für Eingrößen- und Mehrgrößen-Prozesse. Sie enthält die Fuzzy-logischen Regeln für die Überführung der unscharfen Variablen der Eingangsgrößen in unscharfe Fuzzy-Ausgangsvariable (unscharfe Stellgrößen). Dies geschieht mittels der WENN-DANN-Regeln. Das Wissen um das Systemverhalten des Prozesses wird im Fuzzy-Controller durch die folgende Form der WENN-DANN-Regeln in der Regelbasis festgelegt: ${\text{Regel}}\colon \quad \underbrace {WENN\ <{\text{Vorbedingung}}>\quad DANN\ <{\text{Folgerung}}>} _{\text{Fuzzy-Implikation}}$ WENN-Teil (Prämisse) und DANN-Teil (Konklusion) können bei Mehrgrößen-Prozessen mit verschiedenen Fuzzy-Größen (Fuzzy-Variablen) fuzzy-logisch verknüpft sein. Prämisse (lat. praemissa: = vorausgeschickter Satz) = Voraussetzung, Annahme. WENN-Teil einer Regel. Konklusion (lat. conclusio: Folgerung, Schlussfolgerung). DANN-Teil einer Regel. Implikation (lat. implicare: = Ver- oder Einwickeln) = Verknüpfung von Aussagen Sammelbegriff für eine logische Regelaussage (Prämissen → Konklusionen). Eine Fuzzy-logische Regel (= Linguistische Regel = Steuerregel = Produktionsregel) wird als Fuzzy-Implikation bezeichnet. Hier: Ausführung der WENN-DANN-Verknüpfung. Modus ponens (lat. modus: Verfahrensweise, Bedingung, Art und Weise und ponere: stellen, setzen) Modus ponens ist eine Schlussregel, die es erlaubt, aus einer wahren Aussage weitere Aussagen herzuleiten. Die Schlussfolgerung wird wie folgt definiert: Wenn die Aussage A → B wahr ist und zusätzlich A wahr ist, dann muss auch die Aussage B wahr sein. Inferenz (lat. infero: Hineintragen, folgern, schließen). Bedeutung in der Logik: die in einem System von Regeln erzeugte Schlussfolgerung. Umsetzen von fuzzifizierten Eingangssignalen über die Regelbasis zu unscharfen Stellsignalen. Häufig benutzte Operatoren: Max-Min-Inferenz nach Mamdani. (Anwendung: max-Operatoren und min-Operatoren) Aggregation (lat. aggregatio: Anhäufung, Vereinigung) = Zusammenfassung von Daten zu größeren Einheiten. Ausführung aller UND-Verknüpfungen der Prämisse. Zusammenfassung mehrerer Prämissen-Erfüllungsgrade der Regeln. Akkumulation (lat. accumulare: Anhäufen, ansammeln). ODER-Verknüpfung der Implikationsergebnisse μ aller Regeln. (= Zusammenfassung der Erfüllungsgrade μ mehrerer Regeln).

Fuzzifizierung

Bei typischen Anwendungen des Fuzzy-Controllers handelt es sich meist um einen nichtlinearen Prozess mit mehreren Eingangsgrößen, für den das Expertenwissen eines vereinfachten Modells des Prozesses vorliegt.

Der Messbereich eines physikalischen scharfen Eingangssignals wird auf einen geeigneten Wertebereich der Grundmenge der linguistischen Variable (Signalkanal) skaliert. Die Grundmenge wird nach dem Expertenwissen in unscharfe Teilmengen (Fuzzy-Sets) meist überlappend aufgeteilt. Der maximale Zugehörigkeitsgrad für jedes Fuzzy-Set entspricht μ = 1. In Mehrgrößen-Systemen können mehrere Messgrößen und Stellgrößen des Fuzzy-Controllers auftreten.

Die einzelnen Arbeitsschritte lauten:

• Definition der Terme einer Fuzzy-Variablen: Fuzzy-Namen, Anzahl, Art der Fuzzy-Sets und deren Stützpunkte.
• Skalierung der rampenförmigen Beziehungen der Terme zu dem Zugehörigkeitsgrad μ = 1 innerhalb des Messbereiches der Signal-Eingangsgröße. Die linguistischen Terme werden jeweils mit einer Teilmenge dem Messbereich der Eingangsgröße zugewiesen und zwar so, dass der gesamte Messbereich über die gewählte Anzahl der Terme aufgeteilt wird.

Bei Verwendung von dreieckförmigen Fuzzy-Sets ergeben sich 3 Stützpunkte, 2 Fußpunkte innerhalb des Messbereiches eines Signaleingangs auf der Abszisse und einen Kopfpunkt für den Zugehörigkeitsgrad 1 auf der Ordinate. Die unscharfen Mengen der linguistischen Variablen (z. B. Temperatur und deren Terme: kalt, warm, heiß) werden den scharfen Temperatur-Messwerten, meist eine elektrische Spannung, zugeordnet. Die grafische Darstellung einer Fuzzy-Variable als Fuzzy-Set erfolgt meist auf der Abszisse in den scharfen Werten der physikalischen Größe.

Jeder einzelne Signalkanal wird dabei zu einem Vektor von Fuzzy-Mengen und Zugehörigkeitsgraden.

• Die Fuzzy-Sets sind häufig symmetrisch angeordnet und überschneiden sich in den Fußpunkten (Stützpunkten). Typisch sind Überschneidungen von 20 % bis 50 %.

50 % Überschneidung bedeutet, dass das folgende Fuzzy-Set für μ = 0 im Maximum des Zugehörigkeitsgrades μ = 1 des vorherigen Fuzzy-Sets zu steigen beginnt.

• Im Anfangs- und Endbereich der gesamten Fuzzymenge werden meist Teile von trapezförmigen Fuzzy-Sets (Indifferenzbereich) verwendet, um Begrenzungseffekte zu erreichen.

Wenn ein Messwert größer als der größte skalierte linguistische Term „sehr groß“ ist, soll sicher der Zugehörigkeitsgrad 1 sein. Das Gleiche gilt umgekehrt für die Begrenzung des kleinsten linguistischen Wertes „sehr klein“ bzw. bei negativen Werten der Grundmenge „sehr klein negativ“ ebenfalls mit dem Zugehörigkeitsgrad 1. Für einen noch kleineren Eingangsmesswert als „sehr klein“ oder „sehr klein negativ“ bleibt die Zugehörigkeit bei 1.

• Die Anordnung der Fuzzy-Sets auf den Wertebereich der physikalischen Messgröße haben bei einem Eingrößensystem großen Einfluss auf die Gestalt der Eingangs-Ausgangskennlinie (Übertragungskennlinie).

• Große Überschneidungen der Stützpunkte benachbarter Fuzzy-Sets auf der Abszisse bedeutet glatter Kennlinienverlauf (Annäherung zur Linearität).
• 50-%-Überschneidungen benachbarter dreieckförmiger Fuzzy-Sets - sie schneiden sich bei μ = 0,5 - bedeuten lineares Verhalten der Eingangs-Ausgangskennlinie, sofern keine unterschiedlichen Bewertungen mit Faktoren vorliegen.
• Lückende Fuzzy-Sets, die sich in den Fußpunkten nicht überschneiden, führen zu einer Teil-Übertragungskennlinie mit dem Wert null.
• Steilere Rampen gegenüber benachbarten Fuzzy-Sets bedeuten steilerer Teil-Kennlinienverlauf (größere Teilverstärkung).

Inferenz (Datenbasis, Regelbasis)

Fuzzy-Regeln beinhalten das Expertenwissen von Fachleuten, wie anhand von Erfahrungen eine technische Anlage gefahren werden soll. Für die optimale Funktion des Fuzzy-Controllers ist die Wahl der Anordnung der Terme (Fuzzy-Sets) auf der Abszisse des grafischen Modells und der Zugehörigkeit bei der Fuzzifizierung genau so wichtig wie die Aufstellung der Regeln der Regelbasis in der Inferenz-Einheit.

Die Regelbasis enthält die fuzzy-logischen Regeln zur Bestimmung der unscharfen Ausgangsvariablen (unscharfen Stellgrößen) aus den unscharfen Eingangsvariablen.

Grundlage der Fuzzy-Regeln ist die nachstehende Form:

${\text{Regel}}\colon \quad WENN\ <{\text{Vorbedingung}}>\quad DANN\ <{\text{Folgerung}}>$

Die Anwendung der Theorie der Fuzzy-Mengen nach Zadeh – als Fuzzy-logisches Schließen – besagt, aus der Erfüllung einer bestimmten Bedingung eine Schlussfolgerung zu ziehen. Die Bedingung und die Schlussfolgerung mit Fuzzy-Mengen können wie folgt zu sogenannten WENN-DANN-Regeln dargestellt werden, die aus einem WENN-Teil und einem DANN-Teil bestehen.

Die Anwendung der Implikation (Verknüpfung von Aussagen) einer Fuzzy-Arbeitsregel der Regelbasis entspricht einer WENN-DANN-Verknüpfung.

Prämissenauswertung für gleiche Grundmengen

Beispiel der UND-Verknüpfung der Eingangsvariable A und Termen (Fuzzy-Sets) a1 und a2 zur Fuzzy-Ausgangsvariablen U:

$\mu _{u}(U)=\min\{\mu _{a1}(A),\mu _{a2}(A)\}$

Mit dem Minimum-Operator ist gewährleistet, dass die Implikation nicht größer werden kann, als die Prämissenauswertung. Ist beispielsweise das Prämissenergebnis mit dem Zugehörigkeitsgrad μ_a1(A) = 0,5 erfüllt, dann soll auch die Konklusion den Zugehörigkeitsgrad μ_u2(U) = 0,5 aufweisen.

Die Zugehörigkeitsfunktion μ{a1→a2}(A) wird durch den min-Operator einfach dadurch gebildet, dass das Minimum der beiden Erfüllungsgrade nach oben stehender Gleichung gebildet wird.

Beispiel einer Arbeitsregel mit einer Eingangsvariablen und einer Ausgangsvariablen:

${\text{Regel}}\colon \quad \underbrace {\ WENN\quad \underbrace {{\text{ Innentemperatur ist kühl}}\ } _{\text{ Prämisse (Vorbedingung)}}\quad DANN\quad \underbrace {\ {{\text{Heizung auf Mittel}}\ }} _{\text{Konklusion (Schlussfolgerung)}}} _{\text{Implikation (Fuzzy-Regel)}}$

Für die logische Verknüpfung einer Arbeitsregel mit Symbolen A und U für eine Eingangs- und für eine Ausgangsvariable gilt die Aussage:

${\text{Regel}}\colon \quad \underbrace {\ WENN\quad \underbrace {\ A=a1\ } _{\text{ Prämisse}}\quad DANN\quad \underbrace {\ {U=u2\ }} _{\text{Konklusion }}} _{\text{Implikation}}\qquad {\begin{cases}A={\text{Eingangsvariable}}\\U={\text{Ausgangsvariable}}\\{\text{a1 und u2 sind Terme (Fuzzy-Sets)}}\\\end{cases}}$

Die Ein- und Ausgangsvariablen beziehen sich auf je auf eine bestimmte Grundmenge. Die den Variablen A und U zugehörigen Terme a1 und u2 sind Fuzzy-Teilmengen laut Arbeitsregel.

Zu dieser Regel besitzt die Prämisse zu einem bestimmten Zugehörigkeitsgrad μ_a1(A) die Eigenschaft von A. Die Konklusion besitzt zu einem bestimmten Zugehörigkeitsgrad μ_u2(U) die Eigenschaft von U.

Nach der Grundidee von Mamdani (Mamdami-Implikation) darf der Wahrheitsgehalt μ_u2 der Konklusion nicht größer sein, als der Wahrheitsgehalt μ_a1 der Prämisse. Für die Verknüpfung von Erfüllungsgraden gleicher Grundmengen gelten je nach Art der Arbeitsregeln die min oder max-Operatoren.

WENN-DANN-Regel mit mehreren Grundmengen

Beziehungen zwischen unterschiedlichen Grundmengen werden allgemein als Fuzzy-Relationen beschrieben.

Beispiel einer Regel mit zwei Eingangsgrößen und einer Ausgangsgröße:

${\text{Regel}}\colon \quad \underbrace {{\text{WENN Innentemperatur kühl}}\quad UND\quad {\text{Außentemperatur kalt}}} _{\text{WENN-Teil mit 2 Prämissen}}\quad \underbrace {DANN\quad {\text{Heizung max}}} _{\text{DANN-Teil mit Konklusion}}$

Beispiel: Definition einer Fuzzy-Regel mit zwei linguistischen Eingangsvariablen A und B und deren Terme a₁...a_n und b₁...b_n und einer linguistischen Ausgangsvariable U und Termen u₁...u_n:

${\text{Regel}}\colon \quad \underbrace {\ WENN\quad \underbrace {\ A=a2\quad UND\quad B=b1\ } _{\ {\text{2 Teil-Prämissen}}}\quad DANN\quad \underbrace {\ {U=u3\ }} _{\text{Konklusion}}} _{\text{Implikation}}$

Bei unterschiedlichen Grundmengen A und B der Teil-Prämissen werden nur die Antworten von Fuzzy-Mengen auf konkrete Eingangswerte verknüpft.

Fuzzy-Controller mit zwei Eingangsvariablen der Grundmengen Temperatur und Druck mit je drei Fuzzy-Sets und einer Ausgangsvariable U mit vier Fuzzy-Sets

Nach dieser Regel müssen zwei Fuzzy-Eingangsgrößen mit den Variablen A und B in UND-Verknüpfung verarbeitet werden, um den Erfüllungsgrad der Ausgangsvariablen (Konklusion) μ_u(U) zu bestimmen. Der bereits genannte Mamdani-Richtsatz: „Der Wahrheitsgehalt der Konklusion darf nicht größer sein, als der der Prämisse“, erfordert eine kleine Modifikation (d. h. das Abschneiden, Begrenzen) der dargestellten Verarbeitungsregel. Damit wird die Ergebnis-Fuzzy-Menge der Konklusion in Höhe des minimalen Erfüllungsgrades der UND-verknüpften Prämissen mit dem Min-Operator abgeschnitten (begrenzt).

Die vollständige Beschreibung der Problemstellung zur Steuerung eines Prozesses mit den Arbeitsregeln der Regelbasis kann zu einer beträchtlichen Anzahl von Regeln führen, denn es besteht ein exponentieller Zusammenhang zwischen der Anzahl der Regeln und den Variablen mit den zugehörigen Termen wie folgt:

${\text{Anzahl der Regeln}}={\text{(Anzahl der Terme)}}^{\text{(Anzahl der Variablen)}}$

Danach käme man bereits bei 3 Fuzzy-Eingangsvariablen mit je 7 der maximal empfohlenen Anzahl der Terme auf eine maximale Anzahl von 343 Regeln.

Deshalb gilt die Empfehlung zur Aufstellung der Regelbasis: Die Zahl Variablen und der zugehörigen Terme soll so gering wie möglich sein, weil sie insbesondere bei der Berechnung der Erfüllungsgrade und Verknüpfungen von Variablen mit den Fuzzy-Regeln viel Rechenarbeit an einem Microrechner – und nicht zuletzt einen großen Programmierungsaufwand – bedeuten.

Im WENN-Teil einer Regel werden die Terme verschiedener Fuzzy-Veriablen mit den Fuzzy-Operatoren verknüpft. Der WENN-Teil kann eine beliebige logische Verknüpfung mit UND- und ODER-Operatoren von Termen verschiedener Variablen enthalten. Der DANN-Teil mit der Schlussfolgerung ist meist eine einfache Zuweisung eines linguistischen Wertes zu einer unscharfen Ausgangsgröße.

Die UND-Verknüpfung der unscharfen Aussage der Prämisse mit der genannten Regel stellt eine zweistellige Fuzzy-Relation dar. Die Fuzzy-Relation ergibt sich durch die Anwendung des min-Operators:

$\mu _{R}(A,B)=\min\{\mu _{a1}(A),\mu _{b1}(B)\}$

Die Verknüpfung einer Regel mit Teilprämissen kann auch als ODER-Verknüpfung auftreten.

Beispiel: Teilprämissen in ODER-Verknüpfung einer Regel:

${\text{Regel}}\colon \quad \ WENN\quad \underbrace {\ A=a1\quad ODER\quad B=b1\ } _{\ {\text{2 Teil-Prämissen}}}\quad DANN\quad \underbrace {\ {U=u2\ }} _{\text{Konklusion}}$

Die Oder-Verknüpfung der unscharfen Aussage der Prämisse dieser genannten Regel stellt ebenfalls eine zweistellige Fuzzy-Relation dar. Die Fuzzy-Relation ergibt sich durch die Anwendung des Max-Operators:

$\mu _{R}(A,B)=\max\{\mu _{a1}(A),\mu _{b1}(B)\}$

Diese Regel der ODER-Verknüpfung lässt sich auch auf zwei einfache Regeln in UND-Verknüpfung aufspalten:

${\begin{aligned}{\text{Regel 1}}\colon \quad &WENN\quad A=a1\quad DANN\quad U=u2\\{\text{Regel 2}}\colon \quad &WENN\quad B=b2\quad DANN\quad U=u2\end{aligned}}$

Fuzzy-Controller mit zwei Eingangsgrößen e1, e2 und Singletons in der Ausgangsvariablen.

Teilschritte der Inferenz:

Die Inferenz-Einheit von Fuzzy-Controllern bildet mit den unscharfen Termen der Fuzzy-Variablen (Fuzzifizierte Eingangssignale) über die linguistischen Regeln (Regelbasis) die linguistische Schlussfolgerung und besteht aus mehreren Inferenz-Bearbeitungs-Teilschritten. Die Anwendung jeder aktiven Regel liefert auf der Basis des Inferenzschemas die resultierende Ausgangs-Fuzzy-Menge, indem man den Erfüllungsgrad der Regel auf die jeweilige Fuzzy-Menge der Schlussfolgerung überträgt.

Der Erfüllungsgrad ist so definiert, dass er bei der Fuzzy-UND-Verknüpfung so groß ist, wie der kleinste Zugehörigkeitsgrad der Eingangsgrößen. Analog dazu ist der Erfüllungsgrad bei einer Fuzzy-ODER-Verknüpfung so definiert, dass er so groß wie der größte Zugehörigkeitsgrad der Eingangsgrößen ist. Fuzzy-Sets geben für jeden scharfen Wert einer Eingangsgröße den dazugehörigen Erfüllungsgrad einer Fuzzy-logischen Aussage an. Sie stellen eine „Zugehörigkeitsfunktion“ auf.

Das Ziel der Auswertung der Prämisse ist, den Zugehörigkeitsgrad zu jeder Regel zu bestimmen. Sowohl die Prämisse als auch die Konklusion sind als Fuzzy-Mengen definiert.

Es seien die Variablen A mit den Termen a₁, a₂ bis a_i und B mit den Termen b₁, b₂ bis b_i gegeben:

Abhängig von einem scharfen Eingangssignal wird ein bestimmter Fuzzy-Set a_i einer Fuzzy-Variable A mit einer bestimmten Zugehörigkeit μ_a ansprechen. Es können aber auch zwei oder mehrere benachbarte Fuzzy-Sets wie a₁ und a₂ gleichzeitig ansprechen. Dieses Ansprechen der Regeln wird auch mit „feuern“ bezeichnet. Es hängt ganz von der Größe des scharfen Eingangssignals e_i ab, welche und wie viele Fuzzy-Sets feuern.

Bei Mehrgrößensystemen beispielsweise mit den Eingangsvariablen A und B können abhängig von einem scharfen Eingangssignal e₁ einer Grundmenge für A und von einem anderen scharfen Eingangssignal e₂ einer anderen Grundmenge für B jeweils mehrere Fuzzy-Sets gleichzeitig feuern.

Mit der Implikation wirken die aktiven (feuernden) Fuzzy-Sets der Prämisse – je nach UND- oder ODER-Verknüpfung – für jede Regel mit dem min- oder max-Operator begrenzend auf das grafische Modell der Konklusion und dem laut Regel zugehörigen Fuzzy-Set ein (dreieckförmiges Fuzzy-Set wird trapezförmig).

Durch das Ansprechen mehrerer Regeln ergeben sich grafische Teil-Fuzzy-Modelle der Ausgangsgröße, die über die Akkumulation mittels der max-Operatoren zusammengefasst werden.

Defuzzifizierung

Das Inferenzverfahren liefert eine unscharfe Menge einer linguistischen Ausgangsvariable, die sich aus der Vereinigung der einzelnen Ausgangs-Fuzzy-Mengen ergibt. Zur Auswahl eines scharfen Wertes aus einer unscharfen Menge sind verschiedene Verfahren bekannt.

• Maximum-Methode (Mean of maxima)

Bei dieser Methode und deren Varianten wird die gesuchte scharfe Stellgröße aus dem Maximum der akkumulierten Zugehörigkeitsfunktionen gebildet.

Vorteil: einfache Berechnung.

Nachteil: Es werden nur Regeln der Regelbasis berücksichtigt, die das Maximum erzeugen. Abhängig von der Größe der scharfen Eingangssignale sind Sprünge der ermittelten scharfen Stellgröße möglich.

• Flächenschwerpunkt-Verfahren (Center of Gravity)

Diese Methode bildet den Flächenschwerpunktes der Hüllkurve der akkumulierten Zugehörigkeitsfunktionen μ(U) zur skalierten Grundmenge auf der Abszisse. Aus der grafischen Flächenform der Zugehörigkeitsfunktionen wird durch Bildung des Flächen-Schwerpunktes ein Zahlenwert als Abszissenwert errechnet, der der Stellgröße U_S (Indizierung s für Schwerpunkt-Verfahren) entspricht. Kontinuierliche Änderungen der scharfen Eingangsgrößen e₁ bis e_n rufen bei Anwendung dieser Methode kontinuierliche scharfe Stellgrößen U_S hervor.

Bei Fuzzy-Controllern werden zur Defuzzifizierung überwiegend Verfahren zur Bestimmung des Flächen-Schwerpunktes U_S eingesetzt. Dafür gilt die Beziehung des Zugehörigkeitsgrades μ(U) der akkumulierten Ausgangsvariablen U zu den Werten der Abszisse vom Anfangswert U_A bis zum Endwert U_E.

Defuzzifizierung nach dem Flächen-Schwerpunktverfahren mit der numerischen Berechnung.

• Die exakte Berechnung zur Bestimmung des Schwerpunktes einer Fläche U_S lautet:

$U_{S}={\frac {\int \limits _{U_{A}}^{U_{E}}U\cdot \mu (U)dU}{\int \limits _{U_{A}}^{U_{E}}\mu (U)dU}}\qquad {\begin{cases}U={\text{Ausgangsvariable}}\\U_{A}={\text{Flächenanfang für}}\ \mu (U)=0\\U_{E}={\text{Flächenende für}}\ \mu (U)=0\end{cases}}$

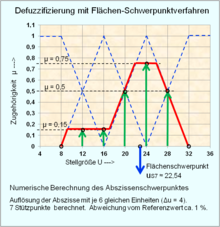
• Methode der numerischen Berechnung des Flächenschwerpunktes einer beliebigen Funktion μ(U):

Die Methode der nummerischen Berechnung des Flächen-Schwerpunktes ist aufwendig. Deshalb werden vereinfachte Verfahren eingesetzt, um den Aufwand der Rechenarbeit und den Speicherbedarf eines Mikrocomputers zu reduzieren.

$U_{S}\approx {\frac {\sum \limits _{i=1}^{n}\Delta U_{i}\cdot \mu _{i}}{\sum \limits _{i=1}^{n}\mu _{i}}}\qquad {\begin{cases}\Delta U_{i}={\text{Werte gleichmäßiger Abstände auf der U-Achse von}}\ U_{A}\ bis\ U_{E},\\\mu _{i}={\text{Werte der Zugehörigkeit (Strichfunktionen) auf der Hüllkurve,}}\\n={\text{Anzahl der}}\ \Delta y_{i}{\text{-Werte (Stützpunkte) von }}\ U_{A}\ bis\ U_{E}.\\\end{cases}}$

Aus dem Beispiel der nebenstehenden Grafik wurde für die eingetragenen Daten mit U_i = 120 ΔU-Elementen zur numerischen Berechnung eingesetzt. Damit ergibt sich der Flächenschwerpunkt mit U_S auf der Abszissenachse als Referenzwert:

$U_{S}\approx {\frac {\Delta U_{1}\cdot \mu _{1}+\Delta U_{2}\cdot \mu _{2}+\cdots +\Delta U_{120}\cdot \mu _{120}}{\mu _{1}+\mu _{2}+\cdots +\mu _{120}}}={\underline {\underline {22,43}}}$

• Vereinfachung der numerische Berechnung durch eine minimale Anzahl von Stützpunkten

Mittels der numerischen Berechnung des Flächenschwerpunktes als scharfe Stellgröße U_S können auch mit wenigen U_i-Werten relativ genaue Flächen-Schwerpunkte erzielt werden:

Beispiel laut der Daten nebenstehender Grafik mit 7 Stützpunkten:

$U_{S}\approx {\frac {\Delta U_{1}\cdot \mu _{1}+\Delta U_{2}\cdot \mu _{2}+\cdots +\Delta U_{7}\cdot \mu _{7}}{\mu _{1}+\mu _{2}+\cdots +\mu _{7}}}$

$U_{S}\approx {\frac {8\cdot 0+12\cdot 0{,}15+16\cdot 0{,}15+20\cdot 0{,}5+24\cdot 0{,}75+28\cdot 0{,}5+32\cdot 0}{0+0{,}15+0{,}15+0{,}5+0{,}75+0{,}5+0}}={\underline {\underline {22{,}54}}}$

Die Abweichung der Berechnung mit 7 Stützpunkten von dem relativ genauen Referenzwert beträgt bei diesem Beispiel ca. 1 % und ist mit dieser Vereinfachung relativ genau, die Abweichungen können bei anderer Kurvenform größer sein.

• Vereinfachung der Flächen-Schwerpunktberechnung mit Strichfunktionen (Singletons)

Defuzzifizierung nach dem vereinfachten Flächen-Schwerpunktverfahren mit Singletons

Eine weitere Vereinfachung einer einfachen Berechnung als Annäherung zur Berechnung des Flächen-Schwerpunktes ergibt sich, wenn die symmetrischen Trapez-Einzelflächen der Gesamtfläche durch die Schwerpunktlage auf der y-Achse und der Flächenhöhe mit μ_i als Werte der Zugehörigkeitsfunktion definiert werden. Dabei wird von rechteckförmigen Elementen ausgegangen. Die Höhe der Rechtecke entspricht dem Erfüllungsgrad μ der jeweiligen Regel. Durch diese Annäherung wird die Überlappung benachbarter dreieckförmiger Fuzzy-Sets zu viel berücksichtigt, was zu einem kleinen Fehler führt.

Approximation der Berechnung des Schwerpunktes durch die Momente der trapezförmigen Einzelflächen:

$U_{S}\approx {\frac {\sum \limits _{i=1}^{n}U_{si}\cdot \mu _{i}}{\sum \limits _{i=1}^{n}\mu _{i}}}={\frac {U_{s1}\cdot \mu _{1}+U_{s2}\cdot \mu _{2}+\cdots }{\mu _{1}+\mu _{2}+\cdots }}\qquad {\begin{cases}U_{si}={\text{Schwerpunktlage der Einzelfläche}}\\\mu _{i}={\text{Trapezhöhe der Einzelfläche}}\\n={\text{Anzahl der trapezförmigen Einzelflächen}}\\\end{cases}}$

Laut dem grafischen Beispiel mit den 2 eingezeichneten Strichfunktionen (Singletons) ergibt sich die Berechnung des Flächenschwerpunktes (Trapez-Höhenverfahren) wie folgt:

$U_{S}\approx {\frac {16\cdot 0{,}15+24\cdot 0{,}75}{0{,}15+0{,}75}}={\underline {\underline {22{,}67}}}$

Dieses Ergebnis bedeutet eine Abweichung gegenüber dem Referenzwert 22,43 von ca. 1 % und ist zufällig immer noch ein sehr gutes Ergebnis mit einer einfachen Berechnungsmethode.

Diese Gleichung entspricht auch der Anwendung der Schwerpunktmethode mit Strichfunktionen (Singletons). Analytische Berechnungen zum Übertragungsverhalten insbesondere die Anwendung der Fuzzy-Controller als Regler in Mehrgrößensystemen haben ergeben, dass mit der Vereinfachung durch Fuzzy-Setz als Singletons aufwendige Rechenzeit erspart werden kann, ohne das Übertragungsverhalten des Fuzzy-Controllers wesentlich zu verschlechtern.

Pro und Contra Fuzzy-Controller

Pro

• Der Fuzzy-Controller als Kennfeldregler beherrscht nichtlineare dynamische Prozesse.
• Ein mathematisches Modell des zu steuernden bzw. zu regelnden Prozesses ist nicht erforderlich.
• Ein unscharfes Modell des Prozesses wird durch Beobachtung und Erfahrungen (Anlagenfahrer, Expertenwissen) aus dem Prozess analysiert.
• Mittels linguistischer Begriffe für Prozesszustände („warm“, „kalt“, „Ventil offen“) werden Produktionsregeln zur Steuerung des Prozesses geschaffen.
• Als Eingrößensystem kann durch die Größe der Überlappung der Fuzzy-Sets einer Fuzzy-Variablen eine Eingang-Ausgang-Kennlinie von linear, kontinuierlich nichtlinear, mit Totzone und Mehrpunkt-Schaltverhalten modelliert werden.
• Fuzzy-Controller können auch von interessierten Laien verstanden werden.
• Robustheit: Parameterabweichungen innerhalb des Prozesses und bestimmter Grenzen werden ohne schädliche Auswirkungen toleriert.
• Mit Einschränkungen kann der Ausfall von einzelnen Signalgebern nicht den gesamten Prozess stören.
• Bei Verwendung von Fuzzy-Chips können Hardware- und Software-Kosten minimiert werden.

Contra

• Der Fuzzy-Controller ist ein statisches System und ist für eine exakte Regelung wegen fehlender dynamischer Anteile einem linearen Standard-Regler weitgehend unterlegen.
• Zur Erweiterung des Fuzzy-Controllers zu einem dynamischen Regler müssen integrale oder differenzielle Anteile von Messgrößen als scharfe Eingangsvariablen für eine gewünschte Dynamik aufbereitet werden.
• Die Stabilitätsprüfung einer exakten Regelung ist schwierig. Bei Vorliegen eines mathematischen Modells der Regelstrecke kann mittels numerischer Berechnung eine Stabilitätsprüfung durchgeführt werden.
• Abhängig von der Anzahl der Variablen (Signal-Eingänge) und der Anzahl der verwendeten Fuzzy-Sets pro Variable und deren exponentiellen Zusammenhänge zur Anzahl der Produktionsregeln können zu einem unübersichtlichen Anwachsen der Fuzzy-Regelbasis führen.
• Der Fuzzy-Controller ist in der Regelungstechnik nicht universell verwendbar, sondern er bezieht sich meist auf die Anwendung der Steuerung eines nichtlinearen Mehrgrößen-Prozesses, der mathematisch schwer zu beschreiben ist.

Fuzzy-Controller und Fuzzy-Regelung

Konventionelle Regelungen

Konventionelle Regelanwendungen mit linearen Regelstrecken sind mit den Standardreglern wie P-, PI-, PD- und PID-Reglern befriedigend zu lösen. Weil der P-Regler ein statischer Regler ist und damit keine Verzögerungsanteile der Regelstrecke kompensieren kann, kommt er selten zur Anwendung. Seine P-Verstärkung muss bei Regelstrecken höherer Ordnung gering bleiben, anderenfalls kommt es zur Instabilität des Regelkreises. Geringe P-Verstärkung bedeutet große Regelabweichung.

Für nichtlineare Regelstrecken sind verschiedene Linearisierungsverfahren bekannt, bei denen ein Modell der Regelstrecke in eine statische Nichtlinearität und in ein dynamisches, lineares Übertragungssystem zerlegt wird. Der einfachste Reglerentwurf erfolgt für eine anspruchsvolle Regelung mittels der Simulation des Regelkreises mit der numerischen Berechnung über die diskretisierte Zeit.

Fuzzy-Regelung

Blockschaltbild eines einschleifigen Regelkreises mit einem dynamischen Fuzzy-Regler

Die typische Anwendung der Fuzzy-Controller sind meist nichtlineare Mehrgrößensysteme, bei denen die Regelgrößen als Eingangsgrößen zurückgeführt werden müssen.

Eingrößen-Fuzzy-Controller weisen eine typische nichtlineare Eingangs-Ausgangsgrößen-Kennlinie auf. Durch die unterschiedliche Anordnung der Fuzzy-Sets (Fuzzifizierung) und der Gestaltung der Regelbasis (Inferenz) kann ein beliebiges prinzipielles Verhalten der Eingangs-Ausgangs-Kennlinie festgelegt werden, wie linear, nichtlinear, mit Totzone und Mehrpunkt-Schaltverhalten. Sie haben keine dynamischen Komponenten. Als Eingrößensysteme sind sie deshalb im Verhalten mit einem Proportional-Regler (P-Regler) vergleichbar, dem abhängig von den linguistischen Variablen und deren Bewertung eine beliebige nichtlineare Kennlinie gegeben wird.

Ein Fuzzy-Controller kann als statischer Eingrößen-Regler unmittelbar für eine unbekannte Regelstrecke benutzt werden, wenn die Ausgangsgröße des Prozesses als Regelgröße in den Regler zurückgeführt wird. Es handelt sich dabei um einen statischen Regler mit einer in weiten Grenzen festzulegenden nichtlinearen Eingangs-Ausgangs-Kennlinie. Ohne Kenntnisse des mathematischen Modells der Regelstrecke ist seine Anwendung begrenzt, da er keine verzögernde Anteile der Regelstrecke kompensieren kann. Regelstrecken mit globalen I-Verhalten können jedoch erfolgreich mit einem Fuzzy-Controller geregelt werden.

Der statische Fuzzy-Controller kann durch Erweiterung mit D- und I-Verhalten ergänzt werden, hat aber bei Vorgabe einer linearen Regelstrecke keinen funktionellen Vorteil gegenüber einem konventionellen PID-Regler. Für die optimale Anwendung in einem Regelkreis ist das mathematische Modell der Regelstrecke erforderlich.

Einem Fuzzy-Controller kann mit entsprechender Gestaltung der Regelbasis auch ein fester Sollwert, oder die Abweichung von einem festen Sollwert eingegeben werden, wodurch in Verbindung mit der Regelstrecke und der zurückgeführten Regelgröße ein Regelkreis entsteht.

Die eigentliche Anwendung des Fuzzy-Reglers als Kennfeld-Regler gilt dem Prozess eines nichtlinearen Mehrgrößensystems mit mehreren Eingangs- und Ausgangsgrößen, dessen mathematisches Modell unbekannt beziehungsweise schwierig zu beschreiben ist. Eine mathematische Fuzzy-Regler-Entwurfsstrategie wie bei den linearen Systemen existiert leider (noch) nicht.

Fuzzy-Controller nach Mamdani und Sugeno

Der prinzipielle Aufbau der Fuzzy-Controller unterscheidet sich in zwei verschiedenen Konzepten:

• Rationale Fuzzy-Controller nach Mamdani.

Die Reglerstruktur besteht aus den Verfahren: Fuzzifizierung scharfer Eingangssignale in linguistischen Mengen, Inferenz mit der Aufstellung der Regelbasis und Defuzzifizierung der Stellgröße meist mit der Flächen-Schwerpunktmethode in scharfe Werte.

• Funktionale Fuzzy-Regler nach Sugeno. (siehe auch Takagi-Sugeno-Regler)

Die Reglerstruktur der Prämisse ist identisch zum rationalen Fuzzy-Regler. Unterschiede zwischen den Strukturen Typ Mamdani und Typ Sugeno liegen in den Regeln der Regelbasis und der Defuzzifizierung der scharfen Stellgröße. Die scharfen Schlussfolgerungen der Stellgrößenwerte erfolgen mit der Wichtung der Regeln der Regelbasis. Der Schritt der Defuzzifizierung aus akkumulierten Fuzzy-Sets existiert nicht. Damit ist eine Reduzierung des mathematischen Aufwandes der Rechenoperationen verbunden, ohne eine erhebliche Verschlechterung der exakten Daten in Kauf zu nehmen.

• Fuzzy-Controller Typ Mamdani mit Singletons

Fuzzy-Controller vom Typ Mamdani mit Singletons der Ausgangsvariablen in der Schlussfolgerung sind laut der grafischen Darstellung der Eingangs- und Ausgangsvariablen anschaulicher, weil die Ausgangsvariablen wie die Eingangsvariablen sich identisch auf die Grundmenge beziehen. Die Ausgangsvariable U mit den Termen ui als Singletons liegen innerhalb der Grundmenge der unscharfen Stellgröße auf der Abszisse, der Erfüllungsgrad μαi zeigt die Amplitude der Singletons.

Die Berechnung der Stellgröße mit Singletons nach Typ Mamdani ist identisch mit Typ Sugeno. Die Regeln der Regelbasis der beiden Berechnungstypen sind unterschiedlich. Für den Typ Sugeno bezieht sich die Schlussfolgerung für jede Regel Ri auf ein Produkt (vorzugebenden Faktor ki) * (Eingangsgröße ei). Dies bedeutet, dass der Stellgrößenbereich durch die Faktoren ki festzulegen ist.

Sugeno-Takagi-Kang-Regler

(Die Reihenfolge der Namen wird in der Fachliteratur auch unterschiedlich geführt, z. B. Takagi-Sugeno-Regler)

Symbol-Definition:
Variablen: A, …, Z
Terme; A = {a₁, a₂, …, a_n}; B = {b₁, b₂, …, b_n}
Konstanten: k₁, k₂, k₃ als beliebige Zahlenwerte >0 innerhalb des Stabilitätsbereiches,
Indizierung: n = 1, 2, … ≪ ∞

Eine Regel der Regelbasis für den Typ Sugeno lautet in der Form linguistischer Begriffe:

$\underbrace {{\text{WENN Temperatur ist warm}}\quad UND\quad {\text{Druck ist mittel}}} _{\text{WENN A = a UND B = b }}\quad \underbrace {DANN\quad {\text{ Ventil = Zahlenwert}}} _{\text{DANN U = f(e1, e2)}}$

Der Wenn-Teil einer Regel der Regelbasis der Fuzzy-Controller ist beim Typ Mamdani mit dem Typ Sugeno identisch.

Der DANN-Teil vom Typ Sugeno unterscheidet sich von dem DANN-Teil des Typs Mamdani dadurch, dass in der Konklusion keine Fuzzy-Menge bestimmt wird, sondern aus den scharfen Werten der Eingangsgrößen e₁...e_n werden über die Prämissenauswertung der Regeln die entsprechenden Erfüllungsgrade μ_α abgeleitet und mit Konstanten k gewichtet.

Die Berechnung der scharfen Stellgröße U_S für einen Regler nullter Ordnung (= keine dynamischen Anteile) vom Typ Sugeno lautet:

$U_{S}={\frac {\sum \limits _{i=1}^{r}U_{i}\cdot \mu _{\alpha i}}{\sum \limits _{i=1}^{r}\mu _{\alpha i}}}={\frac {U_{1}\cdot \mu _{\alpha 1}+U_{2}\cdot \mu _{\alpha 2}+\cdots }{\mu _{\alpha 1}+\mu _{\alpha 2}+\cdots }}\qquad {\begin{cases}U_{i}={\text{Konst. Stellgrößenwert der zugehörigen Regel}}\\\mu _{\alpha i}={\text{Erfüllungsgrad nach min-Operator}}\\i={\text{1 ... r}},\ {\text{Indizierung der Regeln und Erfüllungsgrade}}\\\end{cases}}$

Drei Fuzzy-Sets eines Fuzzy-Reglers mit einer Eingangsvariablen.

Berechnungsbeispiel eines statischen Reglers mit symmetrischer nichtlinearer Kennlinie

Anwendung eines Fuzzy-Reglers

Ein nichtlinearer statischer Regler, dessen Übertragungskennlinie in der Nähe der Regelabweichung eine geringere Verstärkung aufweist als im übrigen Arbeitsbereich, kann eine Regelstrecke mit globalem I-Verhalten besser als ein P-Regler regeln.

Daten:

• Der Regler hat einen Eingangs-Arbeitsbereich (Grundmenge) für eine Regelabweichung e von ± 1.
• Die 3 Fuzzy-Sets werden mit gleichen Gradienten symmetrisch über den Bereich der Grundmenge überlappend angeordnet.
• Die Stellgrößen U werden bewertet mit k1 = 2,5, k2 = 0,4, k3 = 2,5.
• Die Erfüllungsgrade μαi ergeben sich über die Regeln.

Aufstellung der Regelbasis für eine Grundmenge mit 3 linguistischen Teilmengen (Termen):

${\begin{aligned}{\text{Regel 1}}\colon \quad &WENN\quad e={\text{kleiner null}}\quad DANN\quad U1=2{,}5\cdot e\\{\text{Regel 2}}\colon \quad &WENN\quad e={\text{nahe null}}\qquad DANN\quad U2=0{,}4\cdot e\\{\text{Regel 3}}\colon \quad &WENN\quad e={\text{größer null}}\quad DANN\quad U3=2{,}5\cdot e\end{aligned}}$

Eingangs-Ausgangskennlinie eines Fuzzy-Reglers Typ Sugeno

In der nebenstehenden Grafik des Regler-Fuzzy-Modells der Terme ist ein Wert der scharfen Eingangsgröße e = −0,8 eingezeichnet. Es werden die Terme a1 und a2 aktiviert. Damit ergeben sich für die Grundmenge A folgende Zugehörigkeitsgrade:

$\mu _{a}(A)=\{\mu _{a1}=0{,}8;\ \mu _{a2}=0{,}2;\ \mu _{a3}=0\}(A)$

Für die Berechnung der Stellgröße U_S für den Wert der Eingangsgröße e = −0,8 gilt die Gleichung:

$U_{S}={\frac {U_{1}\cdot \mu _{\alpha 1}+U_{2}\cdot \mu _{\alpha 2}}{\mu _{\alpha 1}+\mu _{\alpha 2}}}={\frac {e\cdot k1\cdot \mu _{\alpha 1}+e\cdot k2\cdot \mu _{\alpha 2}}{\mu _{\alpha 1}+\mu _{\alpha 2}}}={\frac {-0{,}8\cdot 2{,}5\cdot 0{,}8-0{,}8\cdot 0{,}4\cdot 0{,}2}{0{,}8+0{,}2}}=-1{,}664$

Ziel dieser Berechnung der Stellgröße U_S ist die Darstellung der Übertragungskennlinie des nichtlinearen Reglers U_S = f(e) zu bestimmen. Dies kann tabellarisch geschehen, indem für die Eingangsgröße e schrittweise Daten im Bereich der Grundmenge von −1 bis 1 vorgegeben werden. Die Zugehörigkeitsgrade für jeden scharfen Wert der Eingangsgröße sind über die angegebenen Geradengleichungen der Rampen zu berechnen.

Die grafische Darstellung der Kennlinie zeigt einen kontinuierlichen nichtlinearen Verlauf. Drei gleiche Bewertungsfaktoren k1 = k2 = k3 = 2,5 würden eine völlig lineare Eingangs-Ausgangskennlinie innerhalb der durch die Fuzzy-Sets festgelegten Begrenzungen ergeben.

Das Verhalten dieses Reglers an einer linearen Regelstrecke mit globalem I-Verhalten wird für den Sollwertsprung W(t) = 4 (= 100 %) und einer Störgröße d(t) = −2 (=-50 %) untersucht.

Regelstrecke:

$G(s)={\frac {(0{,}5\cdot s+1)\cdot (s+1)}{3\cdot s}}$

Fuzzy-Regler: Statischer Eingrößen-Regler mit drei Fuzzy-Sets laut dargestelltem grafischen Fuzzy-Modell Typ Sugeno.

Ergebnis:

Sollwertsprung mit einem Takagi-Sugeno-Regler an einer linearen Regelstrecke mit globalem I-Verhalten und einer statischen Störgröße.

Verhalten des nichtlinearen Reglers laut dargestellter Grafik der Eingangs-Ausgangskennlinie:

• Die Geschwindigkeit des Anstiegs der Regelgröße bis zum Erreichen des Sollwertes ist abhängig von der Verstärkung und von der Größe der Begrenzung der Stellgröße U.
• Die nachlassende Reglerverstärkung um den Bereich von ca. e = −0,2 ... 0,2 führt zu einer schwächeren und damit besseren Dämpfung des Einschwingverhaltens. Dies wird umso deutlicher, wenn die Bewertungsfaktoren von der Eingangsgröße e(t) mit k1 und k3 erhöht würden.
• Die Angriffsstelle der Störgröße d(t) = −2 erfolgt hinter dem I-Glied, vor den beiden Verzögerungsgliedern. Der Verlauf der Regelgröße bricht vorübergehend um den Wert Δy = 1,3 ein.

Fazit:

• Die Anwendung des Fuzzy-Reglers nach Mamdani mit Singletons ist gegenüber dem Verfahren Sugeno übersichtlicher und leichter verständlich. Es werden keine Bewertungsfaktoren benötigt, sondern der Stellgrößenbereich ist mit der Grundmenge der Ausgangsvariablen festgelegt.
• Fuzzy-Regler als statische Eingrößenregler an einer linearen Regelstrecke sind unzweckmäßig, weil der Planungs- und Programmieraufwand hoch ist. Als statischer Regler ist sein Einsatz an linearen Regelstrecken sehr begrenzt. Es können keine Verzögerungsanteile der Regelstrecke kompensiert werden.
• Fuzzy-Regler als statische Eingrößenregler können an einer nichtlinearen Regelstrecke nützlich sein, wenn der kontinuierliche Verlauf der Nichtlinearität der Strecke kompensiert werden soll.
• Dynamische Fuzzy-Regler mit PI- oder PD- oder PID-Verhalten an linearen Regelstrecken sind aufwendiger aber nicht besser als vergleichbare lineare Standard-Regler.
• Dynamische Fuzzy-Regler an unbekannten nichtlinearen Regelstrecken wie z. B. das für Studienzwecke gerne benutzte Modell „Inverses Pendel“ können nützlich sein, wenn das genaue Streckenmodell mathematisch schwierig zu erfassen ist.

Realisierung eines Fuzzy-Controllers bzw. Fuzzy-Reglers

• Die technische Realisierung des Fuzzy-Reglers bzw. eines Fuzzy-Controllers als Hardware erfordert einen programmierbaren Mikrocomputer (CPU), weil geometrische Strecken (Rampen) und logische Funktionen berechnet werden müssen.
• Fuzzy-Logik wird auch für Speicherprogrammierbare Steuerungen kommerziell angeboten.

Literatur

• Winfried Schirotzek, Siegfried Scholz: Mathematik für Ingenieure und Naturwissenschaftler. 3. Auflage. B.G. Teubner, Stuttgart/ Leipzig 1999, ISBN 3-519-00271-X. 
• Gerd Schulz: Regelungstechnik 2, Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzy-Regelung. 2. Auflage. Oldenbourg Verlag München Wien, München 2002, ISBN 3-486-58318-2. 
• Lefteri H. Tsoukalas, Robert E. Uhrig: Fuzzy and Neural Approaches in Engineering. Wiley-Interscience, 1996, ISBN 0-471-16003-2.
• Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik : mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6.