Holomorphe Funktion

In der Mathematik sind holomorphe Funktionen (von altgriechisch ὅλος holos „ganz, vollständig“ und μορφή morphē „Form, Gestalt“) komplexwertige Funktionen (Abbildungen von komplexen Zahlen in komplexe Zahlen), die in der Funktionentheorie, einem Teilgebiet der Mathematik, untersucht werden. Eine komplexwertige Funktion mit Definitionsbereich heißt holomorph, falls sie an jeder Stelle von komplex differenzierbar ist.
Die aus der Schulmathematik bekannten Rechenregeln zum Ableiten vormals reeller Funktionen gelten dabei weiterhin für komplexe Funktionen, obgleich der Holomorphiebegriff viel weitreichendere Konsequenzen nach sich zieht. Anschaulich bedeutet Holomorphie, dass sich die betroffene Funktion an jeder Stelle „fast“ wie eine aus mathematischer Sicht leicht zu verstehende (komplexwertige) lineare Funktion verhält. Erstmals eingeführt und studiert wurden holomorphe Funktionen im 19. Jahrhundert von Augustin-Louis Cauchy, Bernhard Riemann und Karl Weierstraß, obgleich sich die Terminologie der Holomorphie erst im 20. Jahrhundert flächendeckend durchsetzte. Besonders in älterer Literatur werden solche Funktionen auch „regulär“ genannt. Aufgrund ihrer breiten Anwendungsmöglichkeiten zählen sie zu den wichtigsten Funktionstypen innerhalb der Mathematik.
Durch die Möglichkeit der Linearisierung in jedem Punkt ihres Definitionsbereichs können für holomorphe Funktionen , wobei die Menge der komplexen Zahlen bezeichnet, sehr fruchtbare Resultate hervorgebracht werden. Anschaulich kann die mathematische Rechenvorschrift in der Nähe jedes Wertes ihres Definitionsbereichs sehr gut durch die lineare Funktion angenähert werden. Die Annäherung ist dabei so gut, dass sie für die lokale Analyse der Funktion bzw. der Rechenvorschrift ausreicht. Das Symbol bezeichnet dabei die komplexe Ableitung von in . Auch wenn diese Definition analog zur reellen Differenzierbarkeit ist, zeigt sich in der Funktionentheorie, dass die Holomorphie eine sehr starke Eigenschaft ist. Sie produziert eine Vielzahl von Phänomenen, die im Reellen kein Pendant besitzen. Beispielsweise ist jede holomorphe Funktion bereits beliebig oft differenzierbar und lässt sich lokal in jedem Punkt in eine Potenzreihe entwickeln. Das bedeutet, dass man die betreffende Funktion in ihrem Definitionsbereich lokal durch Polynome annähern kann, also unter Verwendung nur der vier Grundrechenarten, wobei zur Konstruktion dieser Polynome nur die Ableitungen der Funktion in einem einzigen Punkt, dem Entwicklungspunkt, benötigt werden. Besonders bei transzendenten holomorphen Funktionen, wie Exponentialfunktionen, trigonometrischen Funktionen (etwa Sinus und Kosinus) und Logarithmen, aber auch bei Wurzelfunktionen, ist dies eine sehr nützliche Eigenschaft, etwa dann, wenn man diese Funktionen und ihre Ableitungen im Entwicklungspunkt gut versteht. Dabei ist zu beachten, dass die genannten Funktionen natürliche Fortsetzungen von den reellen in die komplexen Zahlen besitzen.
Hintergrund der Begriffsstärke der Holomorphie ist, dass die Differenzierbarkeit im Komplexen auf einer offenen „Fläche“ statt nur einem offenen Intervall gelten muss. Dabei müssen beim Grenzübergang zum Differentialquotienten unendlich viele Richtungen (alle Kombinationen aus Nord, Ost, West und Süd) betrachtet werden – eine höhere Anforderung als nur die beiden Richtungen „positiv“ und „negativ“ auf dem reellen Zahlenstrahl. Im Laufe des 19. und 20. Jahrhunderts wurde darauf aufbauend im Rahmen der Funktionentheorie ein eigener Rechenkalkül für holomorphe Funktionen entwickelt. Während Begriffe wie Ableitung, Differenzenquotient und Integral weiterhin existieren, kommen zusätzliche Eigenschaften zum Tragen. Dies betrifft das Abbildungsverhalten holomorpher Funktionen, zusätzliche Techniken in der Integrationstheorie oder auch das Konvergenzverhalten von Funktionenfolgen.
In vielen Teilgebieten der Mathematik bedient man sich der starken Eigenschaften holomorpher Funktionen, um Probleme zu lösen. Beispiele sind die analytische Zahlentheorie, in der über holomorphe Funktionen auf Zahlen rückgeschlossen wird, sowie die komplexe Geometrie oder auch die theoretische Physik. Besonders im Rahmen der Theorie der Modulformen nehmen holomorphe Funktionen eine wichtige Position ein, wobei tiefe Verbindungen zur Darstellungstheorie und zu elliptischen Kurven aufgebaut werden können. Gleich zwei Millennium-Probleme der Mathematik, die Vermutung von Birch und Swinnerton-Dyer und die Riemannsche Vermutung, drehen sich um das Nullstellenverhalten gewisser holomorpher Funktionen.
Einführung[Bearbeiten | Quelltext bearbeiten]
Komplexe Zahlen[Bearbeiten | Quelltext bearbeiten]
Komplexe Zahlen erweitern den Bereich der reellen Zahlen durch Hinzunehmen sog. imaginärer Zahlen. Diese sollen die Eigenschaft haben, algebraische Gleichungen zu lösen, die im Reellen nicht lösbar sind. Ein Beispiel ist die quadratische Gleichung . Sie hat keine reelle Lösung, da das Quadrat einer reellen Zahl stets nicht-negativ ist. Fügt man jedoch den reellen Zahlen eine imaginäre Zahl mit der Eigenschaft hinzu, so kann die obige Gleichung gelöst werden.

Während die reellen Zahlen eine Zahlengerade aufspannen, breiten die komplexen Zahlen eine Ebene aus. Jede komplexe Zahl ist von der Form mit reellen Zahlen und . Geht man Schritte in „reelle Richtung“ und Schritte in „imaginäre Richtung“, so wird die komplexe Zahl mit dem Punkt in der Euklidischen Ebene identifiziert. Dabei wird als Realteil und als Imaginärteil von bezeichnet.
Eine wichtige Eigenschaft komplexer Zahlen ist, dass man mit ihnen, wie im Falle der reellen Zahlen, rechnen kann. Damit ist gemeint, dass Plus, Minus, Mal und Geteilt auch für komplexe Zahlen definiert ist. Um dies umzusetzen, ist lediglich das Beherrschen der reellen Rechenregeln sowie die Regel vonnöten. Die Addition wird in Real- und Imaginärteil separat ausgeführt, also zum Beispiel , und beim Multiplizieren müssen die Klammern verrechnet werden:
Dabei entsteht der Term beim Ausmultiplizieren aus dem Produkt . Auch die Division ist möglich, etwa dadurch, den Nenner durch passendes Erweitern und die dritte binomische Formel reell zu machen:
Somit bilden auch die komplexen Zahlen eine Zahlenstruktur, in der algebraisch gerechnet werden kann. Man sagt auch, dass die Menge der komplexen Zahlen , genau wie die reellen Zahlen , einen Körper bilden.
Komplexe Funktionen[Bearbeiten | Quelltext bearbeiten]
Die Holomorphie ist eine Eigenschaft komplexer Funktionen. Dabei stellt eine Funktion ganz allgemein eine Beziehung zwischen zwei Mengen und über eine Abbildungsvorschrift her. Funktionen müssen die Regel erfüllen, dass jedem Element aus genau ein Element in zugeordnet wird.
Einige Beispiele reeller Funktionen lassen sich direkt auf die komplexen Zahlen übertragen. Dazu zählt etwa die quadratische Funktion .

Reelle Funktionen induzieren Tabellendaten der Form , wobei die Eingabewerte den Definitionsbereich von durchlaufen. Die Analogie zu einer Tabelle entsteht dadurch, dass Daten und in Zeilen- oder Spaltenform zusammengestellt werden können. Es ist jedoch nicht möglich, alle Werte einer reellen Funktion in eine Tabelle einzutragen, da es zum Beispiel bereits nicht möglich ist, alle Werte aufzulisten. Alle nicht leeren, echten Intervalle der reellen Zahlen sind überabzählbar. Daher ist die Darstellung einer reellen Funktion anhand eines Schaubildes üblich. Dabei macht man sich zunutze, dass der Definitionsbereich ein Teil eines Zahlenstrahles ist, ebenso der Wertebereich. Ergo sammeln sich die Informationen zu Punkten in einer zweidimensionalen Ebene. Hebt man diese in der Ebene hervor, bekommt man einen Überblick über das Verhalten einer reellen Funktion.
Für komplexe Funktionen ist die Situation anders. Hier ist bereits der Eingangsbereich eine Fläche. Von daher müsste ein Schaubild nach Art reeller Funktionen vierdimensional sein, was nicht verständlich darstellbar ist.[1] Ein Weg, komplexe, insbesondere holomorphe, Funktionen darzustellen, bedient sich eines Farbschlüssels. Einer komplexen Zahl wird je nach „Himmelsrichtung“ eine Farbe zugeordnet, wobei der Ursprung, also die Null, den Orientierungspunkt bildet. Zusätzlich wird mit der Helligkeit des Farbtons die Größe im Sinne des Abstands zum Ursprung visualisiert. Dabei bedeutet „dunkel“ nahe bei Null, und „hell“ nahe bei „Unendlich“.
-
Der Farbschlüssel, gezeigt durch das Schaubild der Selbstabbildung . In etwa stehen rötliche Farben für komplexe Zahlen, die annähernd positiv reell sind.
-
Schaubild der komplexen Quadratfunktion. Im Zentrum ist ihr Wert 0. Von dort aus nimmt sie links und rechts, also auf der reellen Achse, rote Werte an, denn Quadrate reeller Zahlen sind nie negativ. Von der Mitte startend nach Nord oder Süd ist Türkis präsent: Die Quadrate rein imaginärer Zahlen sind negativ.
-
Die komplexe Fortsetzung der Exponentialfunktion. Ihre Beträge werden mit wachsendem Realteil schnell größer, das Schaubild also heller, und für fallende Realteile kleiner, das Schaubild also dunkler. Parallel zur imaginären Achse des Eingabebereichs ist sie eine periodische Funktion.
Die Darstellung komplexer Funktionen durch Kolorierung ist besonders zur Hervorhebung von Null- oder Polstellen sowie anderer Singularitäten einer Funktion üblich.[2] Die Software Wolfram Mathematica bietet seit Version 12 ein entsprechendes Werkzeug an.[3]
Im Englischen trägt eine solche Art der Visualisierung die Bezeichnung domain coloring. Diese wurde von Frank Farris geprägt.[4] Es gab viele frühere Verwendungen von Farbe zur Visualisierung komplexer Funktionen, typischerweise die Zuordnung von Argumenten (Phasen) zu Farbtönen.[5] Larry Crone verwendete die Methode in den späten 1980er Jahren.[6] Die Technik der Verwendung kontinuierlicher Farbe zur Abbildung von Punkten des Definitionsbereiches in die Zielmenge wurde 1999 von George Abdo und Paul Godfrey verwendet, und farbige Raster wurden in Grafiken von Doug Arnold benutzt, die er auf 1997 datiert.[7] Menschen, die farbenblind sind, können jedoch Schwierigkeiten haben, solche Diagramme zu interpretieren, wenn sie mit Standard-Farbkarten erstellt werden.[8] Dieses Problem kann möglicherweise durch die Erstellung alternativer Versionen unter Verwendung von Farbkarten behoben werden, die in den Farbraum passen, der für Menschen mit Farbenblindheit erkennbar ist. Zum Beispiel kann eine Farbkarte, die auf Blau/Grau/Gelb basiert, für Menschen mit vollständiger Deuteranopie besser lesbar sein als das herkömmliche Schaubild, das auf Blau/Grün/Rot basiert.[9]
Von reeller zu komplexer Differenzierbarkeit[Bearbeiten | Quelltext bearbeiten]

Da mit komplexen Zahlen im Wesentlichen genau wie mit reellen Zahlen gerechnet werden kann, stellt sich die Frage, inwieweit sich die reelle Analysis, mit Begriffen wie Funktionen, Ableitung oder auch Integral, auf die komplexen Zahlen ausweiten lässt.
Im Reellen ist eine Funktion in einem Punkt differenzierbar, wenn sie dort linearisiert werden kann. Das bedeutet, dass sie sich um herum sehr ähnlich zu einer linearen Funktion verhält. Es gilt also für sehr kleine Werte die Approximation , wobei man mit auch erhält. Um die Begriffe „Linearisierung“, „sehr ähnlich“ und „Approximation“ präzise zu fassen, bedient man sich des Konzepts des Grenzwertes. Demnach ist in genau dann differenzierbar, wenn der Differentialquotient
existiert, der auch als Ableitung von an der Stelle bezeichnet wird. Da bei der Berechnung dieses Quotienten nur die Grundrechenarten Addition, Subtraktion und Division verwendet werden, stellt sich die Frage nach einem Analogon im Komplexen. Da die komplexen Zahlen diese Rechnungen auch zulassen, kann die Bedingung
- existiert
eins zu eins übernommen werden. Der entscheidende Unterschied ist hier aber, dass bei der Berechnung des komplexen Differenzenquotienten das kleiner werdende eine komplexe Zahl sein kann. Es kann sich also aus jeder Richtung in der komplexen Ebene genähert werden. Im Gegensatz dazu sind im Reellen nur endlich viele, nämlich zwei, Richtungen möglich, von links () und von rechts ().
Für das Verständnis der komplexen Differenzierbarkeit ist essentiell, den Definitionsbereich der komplexen Funktion auch geometrisch wahrzunehmen. Eingabewerte in die Funktion sind somit nicht bloß komplexe Zahlen, sondern auch Punkte einer Ebene. Auf dieser Ebene ist ein Abstandsbegriff definiert, also können Punkte „nah“ und „weit weg“ zu anderen Punkten liegen. Erst diese Vorstellung erlaubt die Formulierung des für die Differenzierbarkeit essentiellen Lokalitätsbegriffs: Eine in einem Punkt komplex differenzierbare Funktion sieht an Punkten sehr nahe zu einer linearen Funktion „sehr ähnlich“. Genau diese Aussage wird durch den Differentialquotienten analytisch präzisiert. Nach Umformung des Differentialquotienten erhält man
wobei der Fehler in dieser Annäherung „viel kleiner“ ist als der „kleine“ Wert .
Veranschaulichung[Bearbeiten | Quelltext bearbeiten]
Zum Holomorphiebegriff[Bearbeiten | Quelltext bearbeiten]
Ist eine komplexe Funktion in ihrem Definitionsbereich holomorph, bedeutet dies, dass sie in jedem Punkt komplex differenzierbar ist. Wegen der ohnehin restriktiveren Bedingung der komplexen (statt nur reellen) Differenzierbarkeit, gepaart mit deren Gültigkeit für alle Punkte auf einer Fläche statt nur eines Intervalls (einer Linie), ist die Holomorphie eine sehr starke Eigenschaft.
Analytische Motivation[Bearbeiten | Quelltext bearbeiten]
Ein zentrales Problem der Analysis besteht darin, „komplizierte“ Funktionen zu studieren. Dabei bedeutet „kompliziert“ zum Beispiel, dass die Rechenvorschrift nicht aus einer endlichen Abfolge aus Anwendungen der vier Grundrechenarten besteht. Eine in diesem Sinne „einfache“ Vorschrift wäre: Nimm die Eingangszahl mal Zwei, dann das Ergebnis plus Eins, multipliziere dies mit sich selbst, teile dann alles durch die Drei. In Kurzform: . Jedoch lassen sich sehr viele Phänomene in der Natur nicht so einfach beschreiben. Die Mathematik ist demnach bestrebt, Analyseverfahren nichttrivialer Funktionen zu entwickeln. Solche Verfahren kommen zum Beispiel dann zum Einsatz, wenn Änderungsraten bei Naturgesetzen oder Bilanzen in der Wirtschaft erstellt werden müssen. Eine Möglichkeit besteht darin, die Funktion zunächst sehr stark einzuschränken, also nur Eingabewerte aus einem sehr „kleinen“ Vorrat einzusetzen. Klein bedeutet in diesem Kontext, dass die betrachteten Eingabewerte sehr nahe beieinander liegen. Soll eine Funktion etwa um 0 herum studiert werden, würden Werte wie 0,000001 möglicherweise noch in Betracht gezogen, möglicherweise aber nicht mehr 1, geschweige denn 100. In diesem Kontext nennt man die 0 auch den Entwicklungspunkt. Phänomene wie die Holomorphie besagen nun, dass betroffene Funktionen in sehr kleinen Bereichen deutlich verständlicheren Funktionen sehr stark ähneln. Diese verständlicheren Funktionen sind Vorschriften, die sich nur aus den vier Grundrechenarten zusammensetzen. Hinter diesem Prinzip steckt eine gewisse Form der „Stetigkeit“: Wurde eine holomorphe Funktion im Punkt 0 gut verstanden, so lässt sich daraus schon auf ihr Verhalten in z. B. 0,000001 schließen, und das nur anhand der vier Grundrechenarten. Präziser wird die Annäherung über Polynome realisiert, also Ausdrücke wie , und ganz allgemein
Eine holomorphe Funktion kann also um jeden Wert ihres Definitionsbereichs durch Anwendung der Grundrechenarten entwickelt werden. Dabei ist zu beachten, dass es sich bei hinreichend „komplizierten“ Funktionen nur um eine Näherung handelt. Eine zentrale Eigenschaft der Holomorphie ist aber, dass für solche komplizierten Funktionen beliebig lange Polynomketten, also addierte -Terme, zur Annäherung gefunden werden können. Je länger diese Terme sind, desto besser. Lässt man diesen Prozess gegen Unendlich streben, ist die Annäherung in den umliegenden Punkten perfekt, es herrscht also Gleichheit. In diesem Sinne sind also holomorphe Funktionen, zumindest lokal, gerade „unendlich lange Polynome“. Obwohl dabei unendlich viele Terme addiert werden, kann Konvergenz vorliegen, wenn das Funktionsargument nahe genug am Entwicklungspunkt liegt. Wählt man zum Beispiel den Entwicklungspunkt 0 und für die Koeffizienten die Dezimalstellen der Kreiszahl , also
so gilt
Für Werte wird dann „erst recht“ endlich sein. Dabei bezeichnet die Euklidische Länge der Zahl in der Ebene, was dem Abstand zum Punkt 0 entspricht. Diesem Gedanken folgend kann man zeigen, dass Potenzreihen entweder überall oder innerhalb von Kreisscheiben konvergieren. Dennoch kann es sein, dass im Falle der Potenzreihen nicht immer Holomorphie auf ganz vorliegt. Ein Beispiel ist die Funktion , die an der Stelle nicht komplex differenzierbar (ja nicht mal definiert) ist. Jedoch liegt Holomorphie im Bereich aller mit vor, und es gilt mit der geometrischen Reihe
Demnach ist Holomorphie stets zunächst nur eine lokale Eigenschaft.
Es folgen einige Beispiele für holomorphe Funktionen.

Radius = r = 1 beträgt der volle Kreisumfang Längeneinheiten, was auch im dimensionslosen Maß genau 360 Grad entspricht und damit eine Identifizierung des Kreisbogens mit dem einschließenden Winkel erlaubt.
- Eine in der Schule behandelte Funktion, die sich im Allgemeinen nicht durch nur endlichfache Anwendung der vier Grundrechenarten berechnen lässt, ist der Sinus, also die Vorschrift . Hier wird die Vorschrift im Reellen zunächst nicht über eine Zahlenrechnung, sondern geometrisch erklärt. Zur Länge eines Kreisbogens soll die zugehörige gerade Strecke gefunden werden, die den Endpunkt des Bogens mit der Grundachse verbindet, analog beim Kosinus (siehe Bild). Alle betrachteten Strecken haben Längen, im Verhältnis zur Einheit dimensionslos, also entspricht dies einer Abbildung von Zahlen auf Zahlen. Krumme Kreislinien („komplizierte Strecken“) werden auf ungleich lange gerade Linien („einfache Strecken“) abgebildet, was vermuten lässt, dass sich diese Umrechnung nicht in einfacher Weise mit den vier Grundrechenarten darstellen lässt. Es zeigt sich jedoch, dass der Sinus eine holomorphe Funktion ist, weshalb eine Annäherung durch einfache Terme möglich ist. Es gilt zum Beispiel für sehr kleine Werte von
- Dies entspricht einem „Studium“ der Sinusfunktion in oben erklärtem Sinne, da die komplizierte Sinusfunktion durch eine einfache Abbildung angenähert wurde. Dabei war der Entwicklungspunkt 0, in der Tat ist wegen die Annäherung hier perfekt, doch auch für umliegende Werte ist sie brauchbar. Es gilt zum Beispiel und . Für eine exakte Berechnung erhält man für den Sinus
- wobei die Fakultät bezeichnet und das Summenzeichen. Die Formel erweitert sich auf alle komplexen Zahlen und setzt den Sinus dort als Funktion fort, wobei dort keine geometrische Interpretation über Dreiecke mehr zur Verfügung steht.
- Für das lokale Verständnis holomorpher Funktionen werden Polynome herangezogen, jedoch ist die Frage entscheidend, wie man auf die Koeffizienten dieser Polynome schließt, also auf die Zahlen vor den Termen . Dafür werden die komplexen Ableitungen der Funktionen am Entwicklungspunkt benötigt. Genau gesagt gilt eine Formel, die in der Mathematik Taylorreihe genannt wird:
- Hier ist eine Zahl, die nahe am Entwicklungspunkt liegen sollte. Dies lässt sich zum Beispiel an der Wurzelfunktion demonstrieren, etwa um den Punkt . Diese ist dort holomorph, man hat die Ableitungen und . Also gilt mit der Taylor-Formel die Approximation
- für komplexe Zahlen , die nahe an liegen. Der Ausdruck auf der rechten Seite kann, wie oben, durch Anwendung nur der vier Grundrechenarten schnell berechnet werden. Er stimmt nach Einsetzen von exakt mit dem Funktionswert überein, doch auch in der näheren Umgebung von ist die Annäherung noch sehr genau. Man hat etwa
- und es gilt für den exakten Wert . Da Holomorphie eine Eigenschaft komplexer Funktionen ist, gilt die Annäherung auch für nicht-reelle Zahlen in der Nähe von 25. Für erhält man zum Beispiel als Näherung für , und es gilt rückwirkend .
Bedeutung[Bearbeiten | Quelltext bearbeiten]
Die Stärke des Holomorphiebegriffs stützt sich auf folgende Säulen.
- Einfache Handhabung der Taylorpolynome: Durch die Eigenschaft einer holomorphen Funktion, durch Polynome, also Summen von Termen , lokal beliebig gut angenähert werden zu können, ist das Betreiben von Analysis für diesen Funktionstyp besonders einfach. So können etwa sowohl Ableitungen als auch Stammfunktionen der einzelnen Ausdrücke schnell bestimmt werden. Weiß man, dass die Ableitung von ist, so kann man aus bereits folgern.
- Dies ermöglicht es, komplizierte Ableitungen oder Stammfunktionen erneut durch Polynome anzunähern und lokal zu beschreiben.
- Jede Ableitung ist holomorph: Ist eine Funktion holomorph, so auch wieder ihre komplexe Ableitungsfunktion. Wie in einer Kettenreaktion kann gefolgert werden, dass jede holomorphe Funktion bereits unendlich oft komplex differenzierbar ist. Zu dieser Aussage gibt es im Reellen überhaupt keine Entsprechung. So gibt es etwa reelle Funktionen, die zweimal, aber nicht dreimal differenzierbar sind.
- Gleichmäßige Approximation: Die lokale Approximation durch die Polynome erfolgt nicht „willkürlich“, sondern gleichmäßig. Zum Beispiel soll eine holomorphe Funktion auf einer Kreisfläche inklusive Rand bis auf einen Fehler von durch Polynome angenähert werden. Es soll also gelten. Nach Abbruch einer gewissen Schranke im Grad des Polynoms gilt dann für jeden Wert aus der Kreisfläche . Die Annäherung vollzieht sich also nicht unkontrolliert, sondern breitet sich mit „gleicher Geschwindigkeit“ auf Flächen aus. Die untere Bildserie illustriert diese Gleichmäßigkeit bei der Approximation des Sinus um den Nullpunkt anhand seiner Taylorpolynome Bereits im Fall ist um die Null (schwarzer Punkt im Zentrum) eine lokale Ähnlichkeit zu sehen. Erkennbar ist dies an der Farbverteilung und Intensität, die um das Zentrum herum (ganz linkes Bild) sehr ähnelt, etwa „gelb in Nord-Ost“.
-
Komplexer Graph der Sinusfunktion
-
-
-
- Zu beachten ist, dass der ausgesuchte Fehler immer größer als 0 sein muss und die Approximation in der Nähe des Entwicklungspunktes grundsätzlich besser ist. Diese Eigenschaft der gleichmäßigen Konvergenz ist in der Mathematik enorm nützlich. Sie erlaubt es zum Beispiel, dass es bei der Ausführung nichttrivialer Prozesse, wie Ableiten, Integrieren oder unendliches Summieren holomorpher Funktionen, die Reihenfolge vertauscht werden darf. Im Falle unendlich vieler Terme ist dies mathematisch nicht trivial. Beispielsweise erhält man unter Kenntnis der Stammfunktionen von für die Logarithmusfunktion :
- Aus der geometrischen Reihe kann also die Taylorreihe der Logarithmusfunktion in der Nähe von 1 bestimmt werden. In der Umformung wurde der Prozess „die Summe wird integriert“ durch „die integrierten Terme werden summiert“, ersetzt. Dies entspricht der Vertauschung , was wegen der gleichmäßigen Konvergenz der Taylorreihe aber erlaubt ist.

- Wenige Daten reichen aus: Die Regel, dass zwei Punkte eine „Gerade“, also eine lineare Funktion eindeutig bestimmen, gilt auch im Komplexen. Weiter sind es drei Punkte für quadratische Funktionen, vier Punkte für kubische Funktionen, und so weiter. Da holomorphe Funktionen lokal wie „unendlich lange Polynome“ aussehen, besagt dies heuristisch, dass auch hier „verhältnismäßig wenige“ Funktionswerte ausreichen sollten, die Funktion eindeutig zu charakterisieren. Stimmen zwei holomorphe Funktionen auf einer Menge von Zahlen überein, die sich einer Zahl beliebig stark annähern, und gilt auch Gleichheit in , dann sind diese schon lokal identisch. Sie sehen also um den Punkt herum absolut gleich aus. Die Bedingung der Übereinstimmung in unendlich vielen Zahlen wirkt zunächst schwach, es ist jedoch zu beachten, dass es möglich ist, diese Stellen wie aufzulisten. Im Gegensatz dazu kann der Definitionsbereich einer holomorphen Funktion niemals aufgelistet werden, da es sich dabei um zu viele Zahlen handelt. Dazu müssen zwei verschiedene Unendlichkeitsstufen unterschieden werden, nämlich Abzählbarkeit und Überabzählbarkeit. Besonders in Definitionsbereichen, in denen es möglich ist, jeden Punkt durch einen Weg „zu Fuß zu erreichen“, ohne dabei die Fläche zu verlassen, entpuppt sich Holomorphie als sehr stark. Hier genügt die Kenntnis der Funktion in einem lokalen „Ballungsraum“ , um die Funktion im gesamten Bereich eindeutig zu charakterisieren. Würde eine Funktion etwa jedem Punkt des deutschen Festlandes – hier kann man zu Fuß jeden Ort von jedem Startpunkt aus erreichen, ohne Deutschland zu verlassen – einen komplexen Wert zuordnen, und wäre diese überall holomorph, so reichte die Kenntnis im Ballungsraum Hamburg aus, um ihr Verhalten in München oder Passau zu rekonstruieren, obwohl diese Orte weit weg liegen.
Einordnung der Anwendungsmöglichkeiten[Bearbeiten | Quelltext bearbeiten]
Berechnung reeller Integrale[Bearbeiten | Quelltext bearbeiten]
Bedeutsam sind holomorphe Funktionen auch in Anwendungen für reelle Integrale. Es lassen sich einige wichtige Integrale berechnen, ohne eine Stammfunktion angeben zu müssen. Dazu zählt zum Beispiel
- ,
und es ist zu beachten, dass zu keine geschlossene elementare Stammfunktion angegeben werden kann. Integrale wie das obige spielen eine Rolle in der Wahrscheinlichkeitstheorie, hier im Kontext mit der Gaußschen Normalverteilung.
Geschlossene Formeln für unendliche Reihen[Bearbeiten | Quelltext bearbeiten]
In der Analysis, die sich mit Grenzwerten von Funktionen oder Zahlenfolgen beschäftigt, treten auch Reihen auf. Diese sind spezielle Folgen, und werden durch unendliche Summen ausgedrückt. Wenn die Summanden schnell genug klein werden, hat die betroffene Reihe einen Grenzwert. Ein Beispiel ist
Mit holomorphen Funktionen können in manchen Fällen Grenzwerte weit komplizierterer Reihen bestimmt werden. Beispiele sind
- (siehe auch Basler Problem),
- (siehe auch Apéry-Konstante),[10]
aber auch Identitäten wie zum Beispiel die für alle gültige Transformation[11]
Es bezeichnen dabei die Eulersche Zahl und die Kreiszahl. Die letzte Identität geht auf den Mathematiker Carl Gustav Jacobi zurück und hat weitreichende Konsequenzen in der Zahlentheorie. So kann mit ihr etwa gezeigt werden, dass sich jede positive ganze Zahl als Summe von vier Quadratzahlen schreiben lässt,[12] zum Beispiel ist , siehe auch Satz von Jacobi.
In der Zahlentheorie[Bearbeiten | Quelltext bearbeiten]
Holomorphe Funktionen treten in der Zahlentheorie besonders dann in Erscheinung, wenn eine Folge von Zahlen studiert werden soll. Eine Folge ist wie eine Tabelle, wobei den Zahlen jeweils Zahlen zugeordnet werden. Berühmte Beispiele für Folgen sind die Folge der Quadratzahlen , die Folge der Primzahlen oder auch die Fibonacci-Folge Möchte man eine Zahlenfolge mit analytischen Mitteln, also holomorphen Funktionen, untersuchen, kann es helfen, die zugehörige Potenzreihe
zu betrachten. Wie oben gesehen, handelt es sich dabei um eine um 0 holomorphe Funktion, zumindest dann, wenn die nicht zu schnell anwachsen. Es kann gezeigt werden, dass durch die eindeutig festgelegt ist, und umgekehrt. Das bedeutet, dass die erzeugte Funktion gewissermaßen charakteristisch für die Zahlenfolge ist, sie also Eigenschaften der Folge „kodieren“ sollte. Im Allgemeinen ist es jedoch schwer oder nahezu unmöglich, daraus exakte Informationen zu erhalten. Allerdings kann in einigen Fällen das Wachstumsverhalten der für größer werdende ermittelt werden.
Historisches Beispiel ist die Analyse der Partitionsfunktion . Diese ordnet einer natürlichen Zahl die Anzahl der Möglichkeiten zu, diese als Summe kleinerer natürlicher Zahlen zu schreiben. Wegen
gilt . Die Folge der Partitionen wächst schnell an. So gilt bereits und
Lange Zeit galt ein „geschlossenes Verständnis“ dieser Folge als unerreichbar. Godfrey Harold Hardy und Srinivasa Ramanujan studierten intensiv die von den Partitionen (formal setzt man ) erzeugte holomorphe Funktion
-
Die Zahl 5 (blau markiert in obiger Reihe) hat genau 7 Partitionen (rot markiert in obiger Reihe)
-
Allgemeinere schematische Übersicht der ersten Partitionen. Man vergleiche mit den ersten Koeffizienten der Potenzreihe
-
Komplexes Schaubild der Funktion . Am Rand zeichnen sich Bereiche starken Wachstums ab. Diese können genutzt werden, auf die Natur der Koeffizienten der Potenzreihe rückzuschließen
Für jede komplexe Zahl mit ist diese Reihe im Grenzwert endlich (siehe oberes Bild). Es ist keine holomorphe Fortsetzung in den Bereich möglich, dieser Bereich ist in Grau gehalten. Hardy und Ramanujan konnten das Verhalten der Funktion nahe an der Kreislinie mit Radius 1 und Mittelpunkt 0, wo also Konvergenz endet, detailliert beschreiben, und rekonstruierten aus ihren Analysen die asymptotische Schätzformel
die prozentual immer genauer wird, wenn anwächst. Es bezeichnet dabei die natürliche Exponentialfunktion, die Kreiszahl und die Quadratwurzel von 3.
In der Algebra[Bearbeiten | Quelltext bearbeiten]

Viele Anwendungen machen sich die starken Eigenschaften holomorpher Funktionen zu Nutze. So kann zum Beispiel anhand logischer Argumente, die sich auf die grundlegenden Eigenschaften der Holomorphie gründen, bewiesen werden, dass jede in allen komplexen Zahlen holomorphe Funktion, die global beschränkt ist, bereits konstant sein muss. Interessanterweise ist die analoge Aussage im Reellen falsch. So ist zum Beispiel die Funktion in ganz differenzierbar und außerdem beschränkt (da der Nenner niemals kleiner und der Zähler niemals größer als 1 wird), aber ganz offensichtlich keine konstante Funktion . Für reelle Eingaben beschränkte Funktionen wie der Sinus, die überall komplex differenzierbar sind, müssen folglich durch Eingabe beliebiger komplexer Werte über alle Grenzen hinauswachsen. Es gilt zum Beispiel
Mit Hilfe dieser Aussage kann man logisch begründen, dass jede Gleichung der Form
mit und , eine komplexe Lösung besitzt. Das Argument kann exemplarisch am Beispiel
nachvollzogen werden. Die Funktion ist, da sie ein Polynom ist, holomorph für alle komplexen Zahlen. Wegen der Quotientenregel ist auch ihr Kehrwert komplex differenzierbar an Punkten mit , da sonst durch 0 geteilt wird. Geht man davon aus, dass die Gleichung nicht lösbar ist, so ist
ebenfalls auf ganz holomorph. Da als Polynom aber in jeder Richtung für wachsende langfristig beliebig anwächst, kann man folgern, dass beschränkt ist. Damit ist es als global holomorphe Funktion konstant. Das ist offenbar falsch, somit ist ein Widerspruch gefunden, und die Gleichung muss über den komplexen Zahlen lösbar sein.[13]
Dieses Resultat wird auch als der Fundamentalsatz der Algebra bezeichnet.
In der theoretischen Physik[Bearbeiten | Quelltext bearbeiten]
Auch in der theoretischen Physik treten holomorphe Funktionen auf. Ein Anwendungsgebiet betrifft die sogenannte Stringtheorie. Der Ausgangsgedanke dieser Theorie entspringt der „klassischen“ Quantenfeldtheorie (QFT). In der QFT sind die grundlegenden Objekte Teilchen. Während sie sich durch den Raum ausbreiten und miteinander interagieren, beschreiben sie einen Graphen, der als Feynman-Diagramm bezeichnet wird. Diese Diagramme dienen also der Veranschaulichung von Wechselwirkungen zwischen Teilchen, die unsere bekannte Welt aufbauen. In der Stringtheorie sind die grundlegenden Objekte 1-dimensional (Linien bzw. Strings) und nicht 0-dimensional (Punkte bzw. Teilchen). Sie können sich durch den Raum ausbreiten und interagieren, genau wie Punktpartikel, aber anstatt einen Graphen aufzufächern, fächern sie eine Oberfläche auf.[14] Diese Oberflächen können mit Hilfe der Theorie der Riemannschen Flächen beschrieben werden. Das sind zweidimensionale Strukturen im Raum, die lokal wie eine flache Ebene aussehen, deren Koordinaten sich also durch komplexe Zahlen beschreiben lassen. Auf diesen Ebenen können holomorphe Funktionen definiert werden. Diese helfen dabei, alle möglichen Flächen eines Typs zu charakterisieren, wobei nur „geschlossene Flächen mit Henkeln“ interessant sind.
-
Eine Sphäre: Geschlecht 0, also ohne Löcher bzw. „Henkel“
-
Ein Torus: Geschlecht 1
-
Geschlecht 2
-
Geschlecht 3
-
Aus rein topologischer Sicht sieht jeder Torus gleich aus. Sogar eine stetige Umformung in eine Tasse ist möglich.
-
Veranschaulichung der Interaktion zweier Strings auf einem Torus
Obwohl etwa verschiedene Tori (Donuts), Flächen vom Geschlecht 1, aus Sicht der Topologie („Theorie der Formen“) nicht zu unterscheiden sind, können sie als Riemannsche Flächen aufgefasst in eine sehr große Schar verschiedener Klassen unterteilt werden. In diesem Sinne „ungleiche“ Riemannsche Flächen können allgemein durch sogenannte Moduli unterschieden werden. Anschaulich sind Moduli Parameter, in etwa Zahlen, die ohne Doppelungen alle Riemannschen Flächen eines Geschlechts bis auf „holomorphe Äquivalenz“ auflisten. Alle Riemannschen Flächen mit ihren zugehörigen Moduli zu konstruieren, ist ein schwieriges mathematisches Problem. Untersuchungen der Stringwechselwirkungen liefern jedoch deutliche Hinweise darauf, dass die sogenannten world-sheets (dt.: „Weltblätter“) der wechselwirkenden Strings genau diese Konstruktion wiedergeben.[15] Bei world-sheets handelt es sich um Einbettungen von Strings in die Raumzeit.
Historisches zum Begriff[Bearbeiten | Quelltext bearbeiten]
Die Redeweise „holomorph in (einer offenen Menge) “ für „komplex differenzierbar in allen Punkten in “ hat sich in der deutschen Literatur erst in den letzten Jahrzehnten etabliert. Etwa noch bei Marvin Knopp war der Begriff „regulär“ bzw. „analytisch“ üblich. Letzterer wird jedoch in manchen Lehrbüchern bis heute konsequent verwendet, etwa bei Eberhard Freitag. Das Wort „holomorph“ wurde im Jahr 1875 von den Mathematikern Charles Briot und Jean-Claude Bouquet im Rahmen ihres Werkes „Théorie des fonctions elliptiques“ eingeführt.[16] Dabei handelt es sich um das erste Lehrbuch zur Funktionentheorie.[17] Allerdings tauchte „holomorph“ erst in der zweiten Auflage auf; in der ersten Auflage verwendeten sie noch die auf Cauchy zurückgehende Bezeichnung „synectisch“.[16]
Notation[Bearbeiten | Quelltext bearbeiten]
Es werden durchweg folgende Bezeichnungen verwendet:
- , , , und bezeichnen die natürlichen, ganzen, rationalen, reellen bzw. komplexen Zahlen. Zudem bedeutet die offene Einheitskreisscheibe.
- ist eine offene Menge, speziell ist ein Gebiet und die offene Kreisscheibe um mit Radius .
- Das Symbol bezeichnet den Rand der (offenen) Menge . Das Symbol bezeichnet ein geschlossenes Integral, also ein Integral gebildet über eine geschlossene Kurve.
Komplexe Differenzierbarkeit[Bearbeiten | Quelltext bearbeiten]
ℂ als topologischer Raum[Bearbeiten | Quelltext bearbeiten]
Die Euklidische Norm induziert auf den komplexen Zahlen eine Topologie. Analog wie in gilt für die Norm . Eine Menge heißt offen, wenn jeder Punkt innerer Punkt ist. Für jedes gibt es also ein , sodass die Kreisscheibe ganz in liegt. Es gilt also
Für die Definition der komplexen Differenzierbarkeit ist der Begriff der offenen Menge essentiell. Er stellt sicher, dass für jeden Punkt des Definitionsbereichs das Verhalten der Funktion in einer Umgebung dieses Punktes studiert werden kann.
Definition[Bearbeiten | Quelltext bearbeiten]
Es sei eine offene Teilmenge der komplexen Ebene und ein Punkt dieser Teilmenge. Eine Funktion heißt komplex differenzierbar im Punkt , falls der Grenzwert
existiert. Man bezeichnet ihn dann als .[18] Bei dieser Definition ist zu beachten, dass der Limes eine Annäherung aus beliebiger Richtung in der komplexen Ebene darstellt. Äquivalent ist also, dass für jede komplexe Nullfolge , mit für alle , der Wert
existiert und das Ergebnis unabhängig von der gewählten Folge ist.
Zu bemerken ist, dass der Differentialquotient von allen Richtungen gebildet werden kann, da offen ist und somit um jeden Punkt aus eine umliegende Kreisscheibe auch noch in enthalten ist. Ist hinreichend klein, liegt also in , egal welches komplexe Argument besitzt.
Vergleich zur reellen Differenzierbarkeit und die Cauchy-Riemannschen Differentialgleichungen[Bearbeiten | Quelltext bearbeiten]
Jede komplexwertige Funktion lässt sich in der Form schreiben. Dabei sind reellwertige Abbildungen. Man sagt, dass genau dann reell differenzierbar in einem Punkt ist, wenn
wobei die -Fehlerterme, siehe Landau-Symbol, für kleiner werdende gegen 0 gehen. Es gilt also[19]
- für
Dabei handelt es sich bei um reelle Zahlen, die sich über die partiellen Ableitungen der Funktionen und bestimmen lassen. Präziser gesagt, bilden sie die sog. Jacobi-Matrix von als Abbildung von in sich selbst aufgefasst, via
Die reelle Differenzierbarkeit impliziert unter anderem, dass Differentialquotienten existieren, wenn separat die reellen Variablendifferenzen und in bzw. betrachtet werden. Die Richtungsableitungen können sich indes, je nach Gewichtung von und , unterscheiden.
Bei der komplexen Differenzierbarkeit liegt insbesondere reelle Differenzierbarkeit vor, allerdings kommt hinzu, dass die Richtungsableitungen alle identisch sein müssen. Es werden also die Komponenten und zu Gunsten einer zusammenfassenden Komponente „vergessen“. Es gilt im Falle komplexer Differenzierbarkeit an einer Stelle also
- mit .
Die Körperstruktur von erlaubt es, diesen Sachverhalt nach gewohntem Rechenverfahren in die Gleichung
- , wobei ,
umzuwandeln. Spaltet man dies nun rückwirkend in den reellen Fall auf, so ergibt sich mit und die Gleichheit:
- .
Es folgt für die Jacobi-Matrix zwingend die Gleichheit
Dies impliziert
- und
was den Cauchy-Riemannschen Differentialgleichungen entspricht. Eine Funktion ist also genau dann komplex differenzierbar an einer Stelle , wenn sie dort reell stetig differenzierbar ist und zusätzlich die Cauchy-Riemannschen Differentialgleichungen erfüllt.[20] Es ergibt sich daraus, dass die Funktion genau dann holomorph auf ist, wenn sowohl Realteil als auch Imaginärteil überall in stetig partiell differenzierbar sind und die Cauchy-Riemannschen Differentialgleichungen erfüllen.
Holomorphie[Bearbeiten | Quelltext bearbeiten]

Die komplexe Differenzierbarkeit in einem einzelnen Punkt bietet noch nicht viel Struktur. Wichtig für die Funktionentheorie ist der Fall, wenn eine Funktion in ihrer Gänze komplex differenzierbar ist. Die Funktion heißt holomorph in , falls sie in jedem Punkt komplex differenzierbar ist.[21] Ist zudem sogar , so nennt man eine ganze Funktion.[22]
In der Fachliteratur werden die Begriffe holomorph und analytisch häufig synonym verwendet. Dies hat den keinesfalls trivialen Hintergrund, dass eine in holomorphe Funktion eine in analytische Funktion ist, und umgekehrt.[23]
Die Menge der auf einer offenen Menge holomorphen Funktionen wird in der Literatur häufig mit bezeichnet. Diese Schreibweise wird etwa seit 1952 von der französischen Schule um Henri Cartan vor allem in der Funktionentheorie mehrerer Veränderlicher verwendet. Aussagen, es handele sich bei um eine Ehrung des japanischen Mathematikers Oka Kiyoshi, oder eine Reflexion der französischen Aussprache des Wortes holomorph, sind unbestätigt. Vielmehr sei die Notation laut Reinhold Remmert „rein zufällig“, und es heißt in einem Brief von Cartan an Remmert vom 22. März aus dem Jahr 1982:
„Je m’étais simplement inspiré d’une notation utilisée par van der Waerden dans son classique traité ‘Moderne Algebra’“
„Ich habe mich einfach von einer Notation inspirieren lassen, die van der Waerden in seiner klassischen Abhandlung ‚Moderne Algebra‘ verwendet.“
Ableitungsregeln[Bearbeiten | Quelltext bearbeiten]
Sind an einer Stelle komplex differenzierbar, so auch , und . Das gilt auch für , wenn keine Nullstelle von ist. Es gelten ferner Summen-, Produkt-, Quotienten- und Kettenregel.[24]
Winkel- und Orientierungstreue[Bearbeiten | Quelltext bearbeiten]
Eine komplexe Abbildung ist winkeltreu, wenn sie zwei sich in einem Punkt schneidende Geradenstücke auf wiederum zwei Geradenstücke abbildet, die sich im gleichen Winkel schneiden.[25] So sind etwa Drehungen winkeltreue Abbildungen. Es kann gezeigt werden, dass nicht-lokalkonstante holomorphe Funktionen in, bis auf eine diskrete Teilmenge, allen Punkten ihres Definitionsbereichs winkeltreu sind. Es sind durch diese Eigenschaft im Wesentlichen sogar holomorphe Funktionen charakterisiert. Verlangt man zusätzlich noch Orientierungstreue, d. h., dass für die Funktionaldeterminante
in, bis auf eine diskrete Menge, allen Punkten positiv ist, so ist bereits holomorph.[26]
Die Winkeltreue holomorpher Funktionen in einem Punkt lässt sich zudem anhand ihrer Jacobi-Matrix an der entsprechenden Stelle erklären. Dazu muss bekannt sein, dass die Abbildung
nach Einschränkung ihrer Zielmenge auf ihr Bild einen Isomorphismus zwischen Körpern induziert. Wegen Eulers Formel gilt zudem für und die Relation
Eine komplexe Zahl kann demzufolge als lineare Abbildung gedeutet werden, nämlich als eine Drehstreckung, wie die rechte Form als Verkettung von Skalierung und Rotationsmatrix verdeutlicht.[27] Die Cauchy-Riemann-Gleichungen verlangen nichts anderes, als dass die Jacobi-Matrix von dieser Struktur sein soll, wobei dann mit gilt. Darin liegt die Verbindung zu konformen Abbildungen: Winkeltreue bedeutet schlicht, dass die Jacobi-Matrix eine nichtverschwindende Drehstreckung ist.[28]
In Punkten, in denen die Ableitung einer holomorphen Funktion verschwindet, liegt keine Winkeltreue vor, wie man am Beispiel der Funktion mit sieht. Im Nullpunkt werden die Winkel ver--facht.[29]
Analoga zur reellen Analysis[Bearbeiten | Quelltext bearbeiten]
Einige klassische Resultate der reellen Analysis besitzen Pendants im Komplexen.
Mittelwertsatz[Bearbeiten | Quelltext bearbeiten]
Sei eine holomorphe Funktion auf einem konvexen Gebiet , und mit . Dann existieren[30]
so dass
und
Satz von Rolle[Bearbeiten | Quelltext bearbeiten]
Sei eine holomorphe Funktion auf einem konvexen Gebiet , und mit , so dass . Dann existieren[30]
so dass
Regel von L’Hospital[Bearbeiten | Quelltext bearbeiten]
Seien holomorphe Funktionen sowie und und , sowie mit einem . Dann gilt[31]
Integrationstheorie[Bearbeiten | Quelltext bearbeiten]
Komplexe Kurvenintegrale[Bearbeiten | Quelltext bearbeiten]
Die Integrationstheorie im Komplexen unterscheidet sich in einigen Punkten von der im Reellen. Wichtigstes Merkmal ist das Problem, dass es auf einer Ebene unendlich viele Möglichkeiten gibt, sich von einem Punkt zu einem Punkt zu „bewegen“. Im Reellen gibt es (sieht man von nichtigen Rückwärtsbewegungen ab) stets nur eine Möglichkeit entlang des Zahlenstrahls. Die hohe Anzahl an Integrationswegen zwischen und zwingt dazu, den Integralbegriff zum sog. Kurvenintegral auszuweiten. Das bedeutet, dass ein Integral zunächst nicht nur von Anfangs- und Endpunkt, sondern auch von der Wahl der Kurve abhängt.
-
Es gibt wegen des eindimensionalen Zahlenstrahls im Reellen nur eine Möglichkeit, sich von a nach b zu bewegen
-
Bei Kurven in flächenförmigen Definitionsbereichen gibt es viele Möglichkeiten, von a nach b zu gelangen.
-
Im Fall a = b spricht man von einer geschlossenen Kurve. Das Integral wird hier auch mit bezeichnet.
Ist ein Gebiet, stetig und eine unendlich oft differenzierbare (also glatte) Kurve, so definiert man[32]
Das hintere Integral kann nun analog wie im Reellen berechnet werden, etwa durch Aufspalten in die ebenfalls stetigen Komponenten . Hinter dem Differential verbirgt sich die Umformung , die bereits andeutet, dass der Integrationsweg in kleine Intervalle mit unterteilt wird, was den anschaulichen Bogen zur klassischen Integralrechnung schließt.
Integralrechnung[Bearbeiten | Quelltext bearbeiten]
Der Wert eines Integrals
wird bei Endpunkten und im Allgemeinen nicht nur von , sondern auch von der Wahl der Kurve abhängen. Dies ist dann der Fall, wenn die Funktion nicht über eine komplexe Stammfunktion verfügt. Liegt andererseits eine solche vor, gilt[33]

und die letzte Gleichheit zeigt, dass der Wert des Integrals jetzt nicht mehr von abhängt. Analog zum Reellen zeigt es sich, dass der Begriff der Stammfunktion erneut als Umkehrung zum Ableiten gefasst werden kann. Da jedoch der Ausgangspunkt ein Gebiet ist, also eine „Fläche“, muss die Stammfunktion in ganz komplex differenzierbar, also holomorph, sein. Damit ist bereits unendlich oft komplex differenzierbar und es zeigt sich, dass notwendigerweise auch ihre Ableitung eine in holomorphe Funktion gewesen sein muss. Es zeigt sich wieder die Stärke des Holomorphiebegriffes. Aufgrund der „richtungsunabhängigen“ Existenz des Differenzenquotienten ergibt die Berechnung eines Kurvenintegrals ungeachtet der Richtungswahl immer denselben Wert. Man kann dann schreiben
- .
Zwar muss zur Existenz einer Stammfunktion die Funktion notwendigerweise holomorph sein, jedoch ist Holomorphie nicht hinreichend für die Existenz einer Stammfunktion. Wählt man zum Beispiel und , so kann zu keine Stammfunktion gefunden werden.[34] Hintergrund ist, dass es eine „Lücke“ in gibt, in der nicht holomorph ist und daher situationsbedingt Schwierigkeiten bereiten kann. In der Tat besitzt die Logarithmusfunktion kein global holomorphes Pendant in den komplexen Zahlen. Unter zusätzlichen Voraussetzungen an ist jedoch auch die Rückrichtung korrekt. Ganz allgemein dann, wenn ein Elementargebiet ist, besitzt jede holomorphe Funktion eine holomorphe Stammfunktion. In etwa ist jedes Sterngebiet ein Elementargebiet, d. h., es gibt einen zentralen Punkt , von dem aus jeder Punkt durch eine gerade Linie erreicht werden kann, ohne dabei zu verlassen. Beispiel für ein Sterngebiet ist das Innere eines Kreises mit irgendeinem seiner Punkte als Zentrum. Eine Stammfunktion kann dann über
bestimmt werden, wobei hier als Integrationskurve die gerade Verbindungslinie zwischen und gewählt wird.
Es gelten auch im Komplexen die aus der reellen Analysis bekannten Rechenregeln, wie die partielle Integration und die Integration durch Substitution.[35]
Cauchyscher Integralsatz[Bearbeiten | Quelltext bearbeiten]
Ist einfach zusammenhängend, also ein Elementargebiet, und ein Zyklus in , so gilt der Cauchysche Integralsatz[36]
Der Satz gilt also insbesondere dann, wenn ein Sterngebiet und ein geschlossener Weg ist.
Satz von Morera[Bearbeiten | Quelltext bearbeiten]
Nicht jede auf einer offenen Menge holomorphe Funktion besitzt eine Stammfunktion. Allerdings kann gezeigt werden, dass jede holomorphe Funktion eine lokale Stammfunktion besitzt. Dies ist gleichzeitig ein hinreichendes Kriterium für globale Holomorphie. Es stellt zudem eine Umkehrung des Integralsatzes von Cauchy dar, wenn auch in abgeschwächter Form.[37] Ist offen und stetig und gilt für jeden Dreiecksweg , dessen Dreiecksfläche ganz in enthalten ist,
so ist holomorph.[38]
Elementare Folgerungen[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der Integrationstheorie holomorpher Funktionen kann etwas über die Struktur holomorpher Funktionen auf Elementargebieten ausgesagt werden. Ist auf dem Elementargebiet etwa holomorph und nullstellenfrei, existiert eine holomorphe Funktion mit der Eigenschaft . Ein solches wird auch als analytischer Zweig des Logarithmus von bezeichnet.[39]
Eine unmittelbare Folgerung ist die Aussage, dass ebenso eine -te Wurzel, mit , auf besitzt, es gibt also ein holomorphes mit .[40]
Cauchysche Integralformel[Bearbeiten | Quelltext bearbeiten]

Im Jahr 1831 fand Augustin-Louis Cauchy in seinem Exil in Turin[41] eine Integralformel, die erlaubt, eine holomorphe Funktion mit Hilfe der „Randwerte ihres Definitionsbereichs“ zu rekonstruieren. Sie ist von großer Bedeutung in der Theorie holomorpher Funktionen.
Formulierung[Bearbeiten | Quelltext bearbeiten]
Sei offen, die offene Kreisscheibe mit Radius um den Punkt und eine holomorphe Funktion. Liegt dann der Abschluss von noch ganz in , so gilt für alle die Cauchysche Integralformel[42]
Dabei wird die Integrationskurve in mathematisch positivem Sinn, also gegen den Uhrzeigersinn, einfach durchlaufen. Die (stärkere) Version für höhere Ableitungen, mit einem , lautet[43]
Dabei bedeutet die Fakultät von . Der Wert der Funktion (und jeder ihrer Ableitungen) eines Punktes in einem Gebiet hängt also nur von den Funktionswerten am Rand dieses Gebietes ab.
Konsequenzen[Bearbeiten | Quelltext bearbeiten]
Eine Folgerung aus der Cauchyschen Integralformel ist, dass in der komplexen Ebene der Begriff der Analytizität äquivalent zur Holomorphie ist: Jede in holomorphe Funktion ist in analytisch.[44] Umgekehrt stellt jede in analytische Funktion eine in holomorphe Funktion dar.[45]
Eine weitere Folgerung ist die Mittelwertsgleichung
die unter oberen Voraussetzungen gilt. Aus dieser folgt über die Standardabschätzung für Kurvenintegrale
- ,
ein Vorläufer des Maximumprinzips der Funktionentheorie.[46] Sie spielt zudem eine wichtige Rolle bei den Beweisen tieferer funktionentheoretischer Sätze, wie zum Beispiel des Satzes von Liouville oder des Residuensatzes.
Varianten[Bearbeiten | Quelltext bearbeiten]
Die Cauchysche Integralformel lässt sich mannigfach umformulieren. Ist etwa holomorph in einer Umgebung von , so gilt bereits für alle
wobei die Kreiskurve in mathematisch positiver Richtung den Ursprung einfach umläuft. Diese Version wird auch als Schwarzsche Integralformel bezeichnet.[47] Des Weiteren gilt die Formel
unter denselben Voraussetzungen wie oben. Erneut ist zu beachten, dass als Mittelpunkt der Kreisscheibe der Ursprung gewählt wurde.[48]
Diese Integrale lassen sich auch in Polarform schreiben. Ist holomorph auf , dann gilt für die Poissonsche Formel[49]
Diese Formel betont die Beziehung zwischen der Integrationstheorie von Cauchy und harmonischen Analysis.
Potenzreihen im Kontext holomorpher Funktionen[Bearbeiten | Quelltext bearbeiten]
Holomorphie und Analytizität[Bearbeiten | Quelltext bearbeiten]
Ein zentrales Resultat der Funktionentheorie ist, dass holomorphe Funktionen analytisch sind. Das bedeutet, dass sie in jedem Punkt ihres (offenen) Definitionsbereichs in eine Potenzreihe entwickelt werden können, die in einer offenen Kreisscheibe konvergiert und dort die Funktion darstellt.[44] Präziser gilt der Cauchysche Entwicklungssatz: Ist mit offenem , die größte Kreisscheibe um in und holomorph, so ist um in eine Taylorreihe entwickelbar, die in auf kompakten Teilmengen absolut und gleichmäßig konvergiert. Die Koeffizienten sind gegeben durch[44]
- , wobei
Dabei wird der Integrationsweg in mathematisch positiver Richtung einfach durchlaufen. Bemerkenswert ist die Tatsache, dass für den Beweis des Entwicklungssatzes lediglich die Reihenentwicklungen der Funktionen benötigt werden (siehe auch geometrische Reihe), sowie Vertauschbarkeit von Summation und Integration. Für den Fall wurde dies bereits 1831 von Cauchy durchgeführt.[50]
Da jede holomorphe Funktion analytisch ist und umgekehrt, lassen sich Eigenschaften von Potenzreihen direkt auf holomorphe Funktionen übertragen. Dies stellt gleichzeitig den Weierstraßschen Zugang zur Funktionentheorie dar, der die Darstellbarkeit von Funktionen als Potenzreihen zum Ausgangspunkt hat.[51]
Da Potenzreihen beliebig oft komplex differenzierbar sind (und zwar durch gliedweise Differentiation), erhält man insbesondere, dass holomorphe Funktionen beliebig oft differenzierbar[52] und alle ihre Ableitungen wiederum holomorphe Funktionen sind. Hieran erkennt man deutliche Unterschiede zur reellen Differentialrechnung.
Berechnung des Konvergenzradius[Bearbeiten | Quelltext bearbeiten]
Der Konvergenzradius einer außerhalb ihres Entwicklungspunktes irgendwo konvergenten Potenzreihe ist definiert als die Zahl , sodass für alle konvergiert und für alle divergiert.[53] Über das Konvergenzverhalten auf dem Rand der Kreisscheibe kann die Zahl keine Aussage treffen, es kann sehr unterschiedlich sein. Es gilt die Formel von Cauchy-Hadamard[53]
Nach dem Quotientenkriterium hat man im Falle für fast alle :[54]
Dabei darf der Wert ebenfalls durch die Limiten angenommen werden. In den Fällen bzw. ist die betroffene Funktion ganz.
Restgliedabschätzung[Bearbeiten | Quelltext bearbeiten]
Im Falle holomorpher Funktionen kann der Satz von Taylor „effektiv“ gemacht werden. Ist innerhalb einer offenen Menge, die die Kreisscheibe enthält, holomorph, so gilt für alle [55]
Damit folgt für die Restgliedabschätzung
- .
Ist insbesondere hinreichend klein, etwa , so kann dies vereinfacht durch[55]
ausgedrückt werden, wobei die implizite Konstante von und , aber nicht von und abhängt.
Konvergenz und Holomorphiebereich[Bearbeiten | Quelltext bearbeiten]
Grenzen der Darstellbarkeit[Bearbeiten | Quelltext bearbeiten]
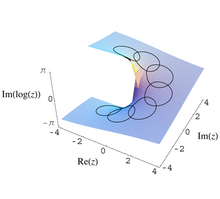
Die Lokalität besagt, dass es nicht sein muss, dass die Potenzreihe die Funktion in ihrem gesamten Definitionsbereich darstellt. Zum Beispiel ist
mit Entwicklungspunkt 0, aber die Reihe konvergiert nur für Werte . In der Tat besitzt die Funktion zur Linken eine Singularität in und ist sonst holomorph in , weshalb der Konvergenzradius der Reihe genau ist. Obwohl also definiert ist, wird die Reihe die Funktion an der Stelle nicht mehr darstellen. Es ist bei dieser Eigenschaft von Potenzreihen auch stets auf die genaue Funktionsvorschrift zu achten. Nur weil die Reihe für solche Werte konvergiert, die nahe genug am Entwicklungspunkt liegen, heißt das nicht, dass dort die Funktion noch nach der ursprünglichen (holomorphen) Vorschrift definiert ist. Zum Beispiel stellt für mit
die Reihe
die holomorphe Funktion nur im Bereich dar, nicht aber in , obwohl sie dort konvergiert. Ein weiteres Beispiel ist mit .[56][57] Zwar konvergiert die zugehörige Potenzreihe um mit Radius , doch stellt sie die Funktion zum Beispiel an nicht mehr dar, obwohl . Hintergrund ist die Festlegung auf den Hauptwert des Logarithmus, der entlang der negativen reellen Achse unstetig verläuft (siehe Bild).
Singuläre Punkte[Bearbeiten | Quelltext bearbeiten]
Es wird eine Potenzreihe
mit Konvergenzradius betrachtet. Ein Randpunkt heißt singulärer Punkt, wenn es keine Umgebung von zusammen mit einer holomorphen Funktion gibt, sodass . Die Menge der singulären Punkte auf bezüglich ist stets abgeschlossen. Ist jeder Punkt in bezüglich ein singulärer Punkt, so entspricht dem Holomorphiegebiet von .[58] Es kann außerdem gezeigt werden, dass die Menge der singulären Punkte auf dem Rand der Konvergenzkreisscheibe niemals leer ist; es gibt also stets mindestens einen singulären Punkt.[59] Zu beachten ist, dass die Potenzreihe in jedem Punkt am Rand ihres Konvergenzbereichs durchaus konvergieren kann. Lediglich eine holomorphe Fortsetzung ist nicht um jeden Punkt des Randes möglich.
Der Lückensatz[Bearbeiten | Quelltext bearbeiten]
Der Lückensatz liefert ein hinreichendes Kriterium dafür, dass die offene Konvergenzkreisscheibe einer Potenzreihe das Holomorphiegebiet der dargestellten holomorphen Funktion ist. Die Potenzreihe
- , wobei
habe den Konvergenzradius . Es gebe eine feste Zahl , sodass die Lückenbedingung
für alle erfüllt ist. Dann ist das Holomorphiegebiet von .[60] Dieser Satz wurde erstmals von Jacques Hadamard im Jahr 1892 gezeigt, wobei der Beweis durch Louis Mordell 1927 stark vereinfacht wurde. Mittlerweile gibt es umfangreiche Literatur und Verallgemeinerungen zum Lückensatz.[60] Bemerkenswerterweise besitzt jede Potenzreihe
mit Konvergenzradius die „Fähigkeit“, zu einer holomorphen Funktion mit Holomorphiegebiet abgewandelt zu werden. Nach einem von Pierre Fatou vermuteten und von Adolf Hurwitz bewiesenen Satz gibt es stets eine Folge , sodass
das Holomorphiegebiet besitzt.[61]
Laurent- und Fourier-Reihen[Bearbeiten | Quelltext bearbeiten]
Satz von der Laurententwicklung[Bearbeiten | Quelltext bearbeiten]
Die Laurent-Reihe verallgemeinert den Begriff der Potenzreihe dahingehend, dass auch negative Exponenten zugelassen werden. Es kann mit dem Cauchyschen Integralsatz für Sterngebiete gezeigt werden, dass sich holomorphe Funktionen auf Ringgebieten in Laurent-Reihen entwickeln lassen.[62] Jede auf einem Ringgebiet
holomorphe Funktion gestattet eine Zerlegung
- ,

wobei und holomorphe Funktionen sind. Mit der Forderung wird diese Zerlegung eindeutig.[63] Insbesondere lassen sich holomorphe Funktionen auf Ringgebieten mit Radien und Zentrum in Laurent-Reihen entwickeln:
Die Reihe konvergiert dabei absolut und lokal gleichmäßig. Eine Berechnung der Koeffizienten ist über die Formel
möglich.[64]
Komplexe Fourier-Reihen[Bearbeiten | Quelltext bearbeiten]
Ein besonderer Fall tritt auf, wenn eine holomorphe Funktion gleichzeitig eine periodische Funktion ist. Dabei reicht es aus, die Periode 1 zu betrachten. Ist auf dem offenen Streifen
holomorph und 1-periodisch, gilt also stets , so besitzt eine Fourier-Entwicklung
Dies ist auf ganz absolut und lokal gleichmäßig konvergent. Eine Berechnung der Koeffizienten ist für jedes durch
möglich.[65] Entscheidend für die Herleitung der Existenz einer Fourier-Reihe auf horizontalen Streifen ist das Abbildungsverhalten der komplexen Exponentialfunktion sowie die Existenz der Laurent-Reihe.[66] Die Entwicklung in Fourier-Reihen spielt eine große Rolle in der Theorie der Modulformen.[67]
Beispiele[Bearbeiten | Quelltext bearbeiten]
Beispiele für holomorphe Funktionen sind Polynome, da diese aus einfachen algebraischen Operationen (Addition und Multiplikation) gewonnen werden. Zum Beispiel ist für die Funktion der Differentialquotient
Es sind diesem Prinzip folgend alle Polynome holomorphe Funktionen. Es stellt sich jedoch die Frage, ob es darüber hinaus noch holomorphe Funktionen gibt und wie diese aussehen. Viele im Reellen differenzierbare Funktionen, wie (außer an der Stelle 0) die Betragsfunktion, sind nicht holomorph. Zum Beispiel gilt
da die rechte Seite, falls existent, keine reelle Zahl ist, die linke jedoch schon.
Jede Polynomfunktion ist eine in ganz holomorphe Funktion. Die Polynomfunktionen sind gerade die Potenzreihen, deren Koeffizienten fast alle verschwinden. Als solche sind sie auch die einzigen ganzen Funktionen, die, falls nicht konstant, im unendlich fernen Punkt eine Polstelle und keine wesentliche Singularität besitzen.[68]
Exponentialfunktion[Bearbeiten | Quelltext bearbeiten]
Die zunächst über den reellen Zahlen definierte natürliche Exponentialfunktion besitzt eine holomorphe Fortsetzung auf ganz . Dort kann sie, wie auch im Reellen, über ihre Potenzreihe definiert werden:
Sie erfüllt für alle die Funktionalgleichung [69] und es gilt , sie ist also gleich ihrer eigenen Ableitung.[70]
Erst über den komplexen Zahlen wird die enge Beziehung zwischen der Exponentialfunktion und den trigonometrischen Funktionen sichtbar. Diese kann mittels der Potenzreihenentwicklungen und einem Vergleich der Koeffizienten hergeleitet werden und zieht wichtige Konsequenzen für die Geometrie der komplexen Zahlen und ganz allgemein in der Mathematik nach sich. Die erstmals von Leonhard Euler gefundene Beziehung, auch Eulersche Formel genannt, lautet
wobei in vielen Anwendungen eine reelle Zahl ist, jedoch auch beliebige komplexe Werte annehmen darf.[69] Daraus folgt insbesondere, dass sie als Funktion -periodisch ist. Es gilt also für alle
- .
Logarithmus[Bearbeiten | Quelltext bearbeiten]
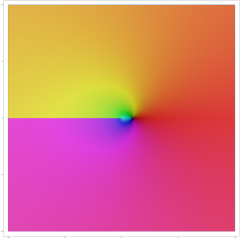
Die komplexe Exponentialfunktion ist global betrachtet nicht injektiv, weshalb sie als ganze Funktion nicht umkehrbar ist. Jedoch kann bei Einschränkung auf den Bereich die Injektivität wieder hergestellt werden. Da dieser Bereich nicht offen ist, so ist etwa kein innerer Punkt, ist es zweckmäßig, auf den offenen Streifen
überzugehen. Es gilt dann[71]
das Bild der Einschränkung entspricht also genau der komplexen Ebene mit Ausnahme der nicht positiven reellen Zahlen. Als bijektive holomorphe Funktion zwischen zwei offenen Mengen ist die Umkehrfunktion, die als Hauptzweig des Logarithmus bekannt ist, wieder holomorph. Diese wird als geschrieben, und es gilt im gesamten Bereich . Der Begriff Hauptzweig motiviert sich daraus, dass die Wahl des Streifens naheliegend, aber keinesfalls eindeutig ist. Es hätte etwa auch der Streifen gewählt werden können – dies liegt in der -Periodizität der komplexen Exponentialfunktion begründet. Der komplexe Logarithmus ist wegen der Eulerschen Formel verwandt zum Hauptzweig des Arguments über die Relation[72]
- .
Dabei bezeichnet den reellen natürlichen Logarithmus. Daraus folgt insbesondere für reelle Zahlen
und die Signumfunktion deutet an, ob sich der Limes von oben oder unten nähert.[73] Es gilt in ganz die Ableitungsformel[74]
Trigonometrische und hyperbolische Funktionen[Bearbeiten | Quelltext bearbeiten]
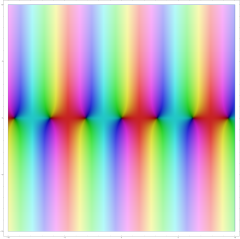
Als Kompositionen aus Exponentialfunktionen sind Sinus und Kosinus bzw. Sinus hyperbolicus und Kosinus hyperbolicus ganze Funktionen.[75][76] Exemplarisch gilt
und dies ist eine ganze Funktion. Im Gegensatz dazu sind die Funktionen Tangens und Kotangens bzw. Tangens hyperbolicus und Kotangens hyperbolicus keine ganzen Funktionen, jedoch in ganz meromorph, also holomorph bis auf eine diskrete Menge von Polstellen. Zum Beispiel hat der Tangens hyperbolicus im Komplexen die Polstellenmenge .
Arkus- und Areafunktionen[Bearbeiten | Quelltext bearbeiten]
Die Arkusfunktionen lassen sich, betrachtet um den Punkt , holomorph in die Einheitskreisscheibe fortsetzen. Man definiert etwa[77]
Der Integrand ist eine in der offenen Einheitskreisscheibe holomorphe Funktion, weshalb das Integral erneut eine holomorphe Funktion darstellt.
Beliebige Potenzfunktionen[Bearbeiten | Quelltext bearbeiten]
Über den komplexen Logarithmus lassen sich beliebige Potenzfunktionen auch im Komplexen verstehen. Diese stellen im Allgemeinen jedoch keine ganzen Funktionen dar.
Ist beliebig, so definiert man für
Dies stellt als Verkettung holomorpher Funktionen eine auf dem Elementargebiet holomorphe Funktion dar. In manchen Anwendungen ist es jedoch von Vorteil, die Unstetigkeitsgerade als die positive reelle Achse zu wählen. Dann setzt man alternativ
Nirgends komplex differenzierbare Funktionen[Bearbeiten | Quelltext bearbeiten]
In keinem komplex differenzierbar und damit auch nirgendwo holomorph sind beispielsweise
- die Betragsfunktion ,
- die Projektionen auf den Realteil beziehungsweise auf den Imaginärteil ,
- die komplexe Konjugation .
Die Funktion ist nur an der Stelle komplex differenzierbar, aber dort nicht holomorph, da sie nicht in einer ganzen Umgebung von komplex differenzierbar ist.
Charakterisierungen des Holomorphiebegriffs[Bearbeiten | Quelltext bearbeiten]
Ist offen, so sind folgende Eigenschaften komplexer Funktionen gleichwertig:[78]
- Die Funktion ist in ganz einmal komplex differenzierbar.
- Die Funktion ist in ganz beliebig oft komplex differenzierbar.
- Real- und Imaginärteil erfüllen die Cauchy-Riemannschen Differentialgleichungen und sind zumindest einmal stetig reell differenzierbar.
- Die Funktion lässt sich überall in lokal in eine komplexe Potenzreihe entwickeln.
- Die Funktion ist stetig und das Wegintegral der Funktion über einen beliebigen geschlossenen zusammenziehbaren Weg verschwindet.
- Die Funktion besitzt lokal eine Stammfunktion, d. h., für jedes gibt es eine Umgebung , sodass eine Stammfunktion besitzt.
- Die Funktionswerte im Inneren einer Kreisscheibe, deren Abschluss in liegt, lassen sich aus den Funktionswerten am Rand mit Hilfe der Cauchyschen Integralformel ermitteln.
- Die Funktion ist reell differenzierbar und es gilt
- wobei der Cauchy-Riemann-Operator ist, der durch definiert ist.[79]
Nullstellen[Bearbeiten | Quelltext bearbeiten]
Im Gegensatz zu beliebigen reell differenzierbaren Funktionen haben holomorphe Funktionen ein sehr kontrolliertes Nullstellenverhalten. Hintergrund ist der sog. Identitätssatz für holomorphe Funktionen, der sicherstellt, dass eine auf einem Gebiet nicht konstante holomorphe Funktion in dessen Innerem keine Werte häufen kann. Insbesondere gilt: Ist und holomorph und nicht konstant, so ist jede der Fasern genannten Urbilder
lokal endlich in , und es folgt, dass nur höchstens abzählbar viele sog. -Stellen besitzt.[80] Von besonderem Interesse ist , also gerade die Nullstellen von .
Satz von Rouché[Bearbeiten | Quelltext bearbeiten]
Es seien holomorphe Funktionen auf einem Elementargebiet und eine stückweise glatte geschlossene Kurve in , sodass diese jeden Punkt in deren Innerem genau einmal positiv umläuft. Es gelte für alle . Dann haben die Funktionen und keine Nullstellen auf und, mit Vielfachheit gerechnet, gleich viele Nullstellen im Innern der Kurve.[81]
Der Satz von Rouché kann auch auf meromorphe Funktionen ausgeweitet werden.
Jensensche Formel[Bearbeiten | Quelltext bearbeiten]
Die Jensensche Formel stellt einen Zusammenhang zwischen dem Wachstum einer holomorphen Funktion auf Kreisrändern und deren Nullstellenverteilung her. Ist eine auf einem Gebiet holomorphe Funktion, sodass die Kreisscheibe enthält, und sind die Nullstellen von in (bei Vielfachheit mehrfach wiederholt), so gilt mit bereits[82]
Eine Verallgemeinerung stellt die Poisson-Jensen-Formel dar, die unter obigen Voraussetzungen für jedes mit anwendbar ist:[82]
Sie spielt eine wichtige Rolle beim Beweis des Produktsatzes von Hadamard für holomorphe Funktionen, zum Beispiel im Umfeld von L-Funktionen.
Singularitäten[Bearbeiten | Quelltext bearbeiten]
Holomorphie einer Funktion auf einer offenen Menge ist eine starke Eigenschaft und zieht viele Konsequenzen hinsichtlich Integrationstheorie oder Abbildungseigenschaften nach sich. So strahlt die Analytizität in einem Punkt stets auf umliegende Punkte aus. Es kann die Frage gestellt werden, was ausgehend von einem bestimmten Punkt einer offenen Menge über das Verhalten einer holomorphen Funktion ausgesagt werden kann. Dabei befindet sich im Innern von und liegt damit isoliert in einer lückenlosen Menge von Punkten, auf denen ein aus analytischer Sicht sehr starkes Verhalten hat. Man bezeichnet ein solches auch als isolierte Singularität.[83]
Es ist ein wichtiges Resultat, dass die holomorphe Funktion „um herum“ nur drei verschiedene Arten von Verhalten aufweisen kann. Exemplarisch sind die Funktionen
- , und
allesamt holomorph in , weisen aber um den Nullpunkt herum ein sehr unterschiedliches Verhalten auf.[83]
Der Typ einer Singularität lässt sich eindeutig aus den Koeffizienten der in ihr entwickelten Laurent-Reihe der Funktion ablesen.[84]
Hebbare Singularität[Bearbeiten | Quelltext bearbeiten]
Eine hebbare Singularität in einem Punkt liegt vor, wenn die holomorphe Funktion um herum beschränkt ist, also „ganz normales“ Verhalten aufweist. Es ist also für alle in einer hinreichend kleinen punktierten Umgebung von in . Nach dem Riemannschen Hebbarkeitssatz kann in einem solchen Fall immer stetig, ja sogar holomorph, auf ganz fortgesetzt werden.[85] Es gibt also eine holomorphe Funktion , die auf ganz mit übereinstimmt.[83]
Beispiele für Funktionen mit hebbaren Singularitäten sind
- an der Stelle , holomorphe Fortsetzung ist ,
oder auch
- an der Stelle , holomorphe Fortsetzung ist der Kardinalsinus, mit der Potenzreihenentwicklung .
Polstelle[Bearbeiten | Quelltext bearbeiten]

Eine holomorphe Funktion hat eine Polstelle der Ordnung in , falls sie in einer Umgebung von als Quotient
mit einem holomorphen mit geschrieben werden kann.[86] Eine Polstelle beliebiger Ordnung lässt sich zudem durch das lokale Abbildungsverhalten von charakterisieren. Es hat genau dann einen Pol in , falls gilt
- .
Das Merkmal einer Polstelle ist also, dass sich die Punkte in einer Umgebung nicht chaotisch verhalten, sondern in einem gewissen Sinne gleichmäßig gegen Unendlich streben.[87]
Ist eine Polstelle der Ordnung von , so hat die Laurent-Entwicklung von um diese notwendigerweise die Gestalt
Eine solche Entwicklung ist gleichzeitig hinreichend für die Existenz eines Pols der Ordnung .[84]
Beispielsweise hat die auf holomorphe Funktion einen Pol vierter Ordnung in .
Wesentliche Singularität[Bearbeiten | Quelltext bearbeiten]

Eine Singularität wird als wesentlich bezeichnet, wenn sie weder hebbar noch Polstelle ist.[87] Sie lässt sich über den Satz von Casorati-Weierstraß charakterisieren, der besagt, dass eine holomorphe Funktion in jeder punktierten Umgebung einer wesentlichen Singularität jeder beliebigen komplexen Zahl beliebig nahe kommt. Zu jeder punktierten Umgebung im Definitionsbereich von und zu jedem gibt es also für alle ein mit .[88]
Alternativ lässt sich eine wesentliche Singularität an den Koeffizienten der Laurent-Reihe ablesen. Genau dann wenn um die Laurent-Reihe
mit für unendlich viele besitzt, ist eine wesentliche Singularität.[84]
Meromorphe Funktionen[Bearbeiten | Quelltext bearbeiten]
Formal wird das Symbol definiert. Eine Abbildung heißt meromorphe Funktion, falls die Menge diskret in liegt, die Einschränkung holomorph ist und jeder der Punkte aus eine Polstelle von ist.[89]
Nimmt man also die isolierten Polstellen einer holomorphen Funktion „mit in den Definitionsbereich auf“, so spricht man allgemein auch von einer meromorphen Funktion. Der Zusammenschluss aller auf einem Gebiet meromorpher Funktionen bildet einen Körper.[89] Dabei werden Polstellen als Kehrwerte von Nullstellen aufgefasst, wobei der Wert Unendlich mittels der stereographischen Projektion auf die Riemannsche Zahlenkugel als „Nordpol“ interpretiert werden kann,[90][91] woher auch die Bezeichnung Polstelle rührt.
In einigen Anwendungen ist die Voraussetzung der Holomorphie zu restriktiv. Zum Beispiel sind alle holomorphen elliptischen Funktionen zu einem beliebigen Gitter bereits konstant.[92] Erst beim Übergang zu auf ganz meromorphen elliptischen Funktionen erhält man nichttriviale Beispiele, wie etwa die Weierstraßschen p-Funktionen.[93] Auch einige andere sehr wichtige Funktionen, wie die Riemannsche Zetafunktion und die Gammafunktion, sind auf nicht holomoroph, sondern lediglich meromorph.
Residuenkalkül[Bearbeiten | Quelltext bearbeiten]
Das Residuum[Bearbeiten | Quelltext bearbeiten]
Ist die Funktion auf einer punktierten Kreisscheibe holomorph, so kann sie um in eine Laurent-Reihe
entwickelt werden. Das Residuum bezieht sich auf den Term in dieser Reihe, der keine Stammfunktion auf besitzt, nämlich Es definiert jedoch nicht diesen Term, sondern lediglich den zugehörigen Koeffizienten, man schreibt[94]
Das Residuum ist ein Funktional, d. h. eine lineare Abbildung vom Raum der holomorphen Funktionen in die komplexen Zahlen.
Residuensatz[Bearbeiten | Quelltext bearbeiten]

Der Residuensatz gehört zu den zentralen Sätzen der Funktionentheorie. Er besagt, dass das geschlossene Kurvenintegral einer holomorphen Funktion in einem Elementargebiet ohne eine diskrete Menge an Singularitäten nur von den isolierten Singularitäten des Integranden und den Windungszahlen der Integrationskurve abhängt. Damit wird durch ihn die Integralformel von Cauchy verallgemeinert. Da in vielen Fällen die Behandlung der isolierten Singularitäten unkompliziert ist, kann er zu einer schnellen Berechnung von Integralen beitragen, selbst wenn keine Stammfunktion gefunden werden kann.
Präzise besagt der Residuensatz, dass, falls ein Elementargebiet ist, eine -elementige Teilmenge, holomorph, und eine stückweise glatte, geschlossene Kurve, dann gilt die Residuenformel[94]
wobei die Umlaufzahl von rund um bezeichnet. Der Wert des Integrals hängt also nur von den Residuen der Funktion und deren Umlaufzahl ab.
Bedeutung[Bearbeiten | Quelltext bearbeiten]
Der Residuensatz zieht einige wichtige Folgerungen für die Funktionentheorie nach sich. Es werden ein paar in der Literatur übliche Anwendungen angeführt.
Null- und Polstellen zählendes Integral[Bearbeiten | Quelltext bearbeiten]
Ist eine auf einem Elementargebiet meromorphe Funktion und umschließt die stückweise glatte geschlossene Kurve alle Null- und Polstellen von genau einmal in mathematisch positiver Richtung, so gilt für die Anzahl von Null- und Polstellen bzw. die exakte Formel[95]
Explizite Berechnung von Integralen[Bearbeiten | Quelltext bearbeiten]
Der Residuensatz kann in manchen Fällen zur Berechnung von Integralen, zum Beispiel über rationale Funktionen, dienen. Ein Beispiel ist die für ganze Zahlen gültige Formel[96]
Auch kann er zur Berechnung der Partialbruchzerlegung des Kotangens,[97] zur Lösung des Basler Problems[98] und zum Beweis der Formel[99]
herangezogen werden. Auch die explizite Berechnung Fresnelscher Integrale ist mit dem Residuensatz möglich.[100]
Abbildungseigenschaften[Bearbeiten | Quelltext bearbeiten]
Identitätssatz[Bearbeiten | Quelltext bearbeiten]

Es zeigt sich, dass eine holomorphe Funktion schon durch sehr wenig Information eindeutig bestimmt ist. So genügt es bereits, dass zwei auf einem Gebiet holomorphe Funktionen und auf einer Teilmenge übereinstimmen, die einen Häufungspunkt in hat, um global zu folgern. Dabei ist ein Häufungspunkt der Teilmenge , falls in jeder noch so kleinen offenen Umgebung von unendlich viele Elemente von liegen. Betont sei an dieser Stelle die Bedingung, dass sich der Häufungspunkt innerhalb des Gebietes befinden muss. Wird dies nicht gefordert, ist die obere Aussage im Allgemeinen falsch.
Präziser lässt sich zeigen, dass folgende Aussagen äquivalent sind:[101]
- .
- Die Koinzidenzmenge hat einen Häufungspunkt in .
- Es gibt einen Punkt , sodass für alle ganzen Zahlen die Gleichheit gilt.
Beim Identitätssatz ist die Bedingung an , ein Gebiet zu sein, wichtig, da Holomorphie eine lokale Eigenschaft ist. Zum Beispiel stimmen die beiden holomorphen Funktionen
und
sogar auf ganz überein, sind jedoch global betrachtet nicht gleich, da . Es ist kein Gebiet, da es als disjunkte Vereinigung nicht leerer offener Mengen geschrieben werden kann. Ebenfalls wichtig ist, dass der Häufungspunkt ein Teil des Gebietes ist. So ist etwa die Funktion holomorph in und nimmt den Wert 0 für alle an, stimmt aber nicht mit der Nullfunktion überein. Es ist zu beachten, dass der Häufungspunkt 0 der Folge nicht Teil von ist.[102]
Satz von der Gebietstreue[Bearbeiten | Quelltext bearbeiten]
Einfach gesprochen sagt der Satz von der Gebietstreue, dass eine nicht konstante holomorphe Funktion Gebiete in Gebiete überführt.
Ist ein Gebiet und holomorph und nicht konstant, so ist wieder ein Gebiet. Dieses Offenheitsprinzip ist für stetige Funktionen, bei denen lediglich Urbilder offener Mengen offen sein müssen, im Allgemeinen nicht richtig. Es scheitert beispielsweise bereits bei differenzierbaren Funktionen in den reellen Zahlen, wo der Sinus den nicht offenen Wertevorrat besitzt.[103]
Beim Beweis des Satzes von der Gebietstreue geht als wichtiger Zwischenschritt das lokale Abbildungsverhalten nichtkonstanter holomorpher Funktionen ein, siehe unten. Im Reellen scheitert die Aussage, dass eine Umgebung von 0 auf eine Umgebung von 0 abbildet, zum Beispiel ist hier stets .
Als einfache Folgerungen des Satzes der Gebietstreue ergibt sich, dass eine auf einem Gebiet holomorphe Funktion , für die entweder , oder konstant ist, bereits konstant sein muss.[104]
Es existiert auch eine quantitative Version des Satzes der Gebietstreue.[105]
Lokales Abbildungsverhalten[Bearbeiten | Quelltext bearbeiten]
Es kann gezeigt werden, dass sich jede nichtkonstante holomorphe Funktion im Wesentlichen wie eine Potenz verhält. Genauer gesagt gilt: Ist nichtkonstant und holomorph in einem Gebiet um 0 und gilt , so existiert eine natürliche Zahl , eine kleine Umgebung um die 0, eine biholomorphe Abbildung mit , sodass
für alle .[104] Insbesondere folgt nach dem Variablenwechsel die Identität
für alle . Die Zahl ist dabei eindeutig bestimmt. Insbesondere ist genau dann lokal biholomorph, wenn gilt.
Maximumprinzip und verwandte Aussagen[Bearbeiten | Quelltext bearbeiten]
Maximum- und Minimumprinzip[Bearbeiten | Quelltext bearbeiten]
Eine Folgerung des Satzes über die Gebietstreue ist das sog. Maximumprinzip. Dieses sagt aus, dass eine auf einem Gebiet holomorphe Funktion , die im Innern von ein lokales Maximum bei annimmt, bereits konstant sein muss. Existiert zu also eine offene Umgebung , sodass für alle , so ist konstant. Dieses Prinzip kann auch anders formuliert werden: Jede nichtkonstante holomorphe Funktion auf einem beschränkten Gebiet mit stetiger Fortsetzung auf den Rand nimmt auf diesem ihr Maximum an. Dabei ist die Beschränktheit des Gebietes von zentraler Bedeutung. Ist nämlich unbeschränkt, so ist die Aussage in dieser Form nicht mehr gültig. Betrachtet man beispielsweise die Funktion , so gilt
wobei . Damit stellt man fest, dass zwar auf dem Rand des Streifens beschränkt ist, jedoch in dessen Innerem für über alle Grenzen hinauswächst. Als Beweis des Maximumsprinzips reicht die Erkenntnis, dass nach dem Satz der Gebietstreue jeder Punkt in ein innerer Punkt ist, womit es in seiner Umgebung aber stets Punkte gibt, deren Betrag größer als ist.[106]
Verwandt zum Maximumsprinzip ist das Minimumprinzip. Ist wie oben nicht konstant und hat es ein Betragsminimum in , so muss notwendigerweise eine Nullstelle von sein.[107]
Satz von Phragmén-Lindelöf[Bearbeiten | Quelltext bearbeiten]


Der Satz von Phragmén-Lindelöf, von Lars Phragmén und Ernst Lindelöf im Jahr 1908 publiziert,[108] kann als eine Erweiterung des Maximumprinzips angesehen werden. Er gibt nun ein Kriterium, mit dessen Hilfe Beschränktheit der Funktion innerhalb ihres unbeschränkten Definitionsgebiets gefolgert werden kann. Sei ein Elementargebiet und holomorph. Es gebe eine holomorphe Funktion , die keine Nullstellen hat und zudem beschränkt ist. Der Rand, einschließlich eines unendlich fernen Punktes , zerfalle in Teile , sodass für eine Konstante gilt:
- Für jedes ist .
- Für jedes und ein festes gilt .
Dann gilt bereits für alle .[109] Das Symbol bezeichnet den Limes superior.
Eine andere Variante des Satzes besagt: Sei stetig auf dem Streifen und holomorph in dessen Innerem. Es gelte für alle Randwerte , also mit oder , und es gebe Konstanten und mit
Dann gilt auch im Innern des Streifens.[110] Dass der Satz für nicht mehr stimmt, zeigt das weiter oben angeführte Beispiel .
Es existiert eine Variante des Satzes für Kreissektoren. Es sei dafür holomorph auf dem Kreissektor , mit stetiger Fortsetzung auf . Ferner gelte auf dem Rand von und es gebe Konstanten mit für alle . Dann gilt bereits für alle .[111]
Der Satz von Phragmén-Lindelöf hat Anwendung unter anderem in der Theorie der L-Funktionen. Mit seiner Hilfe kann deren Wachstumsverhalten im sog. kritischen Streifen analysiert werden, etwa im Rahmen des Heckeschen Umkehrsatzes.[112]
Hadamardscher Dreikreisesatz[Bearbeiten | Quelltext bearbeiten]
Das Verhalten der Betragsmaxima einer holomorphen Funktion auf Kreislinien innerhalb eines Ringgebiets ist konvex bezüglich der logarithmierten Radien. Ist also holomorph auf dem abgeschlossenen Ringgebiet , mit dem Ursprung als Mittelpunkt, und definiert man
so gilt stets[113]
Diese als Hadamardscher Dreikreisesatz benannte Aussage ist verwandt zu Sätzen über holomorphe Funktionen auf Streifen. Ist holomorph und beschränkt auf einem Streifen , so ist die Funktion
konvex.[114] Diese Feststellung lässt sich auf den Fall höchstens polynomiell wachsender Funktionen weiter übertragen. Sei in dieser Situation durch ein Polynom beschränkt, und bezeichne zu jedem die kleinste Zahl mit
für alle . Dann ist eine konvexe und insbesondere stetige Funktion auf , sofern endliche Ordnung auf dem Streifen hat.[113]
Diese Aussagen sind zum Beispiel im Umkreis der Lindelöfschen Vermutung bezüglich der Riemannschen Zeta-Funktion von Interesse.[115]
Werteverteilungen[Bearbeiten | Quelltext bearbeiten]
Ganze Funktionen[Bearbeiten | Quelltext bearbeiten]
Satz von Liouville[Bearbeiten | Quelltext bearbeiten]

Der Satz von Liouville besagt, dass jede beschränkte ganze Funktion bereits konstant ist. Im Umkehrschluss bedeutet dies, dass jede nicht-konstante ganze Funktion bereits unbeschränkt sein muss, langfristig also, im Absolutbetrag betrachtet, über alle Schranken wachsen wird. Zwar ist zum Beispiel die Funktion im Reellen beschränkt, wird aber auf ganz betrachtet beliebig anwachsen. Der Satz wurde erstmals von Joseph Liouville im Jahr 1847, damals allerdings nur im Rahmen der Liouvilleschen Sätze im Spezialfall für elliptische Funktionen, bewiesen.[116]
Der Satz von Liouville ist eine Folgerung aus der verallgemeinerten Cauchyschen Integralformel. Gilt , so folgt mittels der Standardabschätzung für Integrale für alle und Radien :
Dabei entstammt der Term der Bogenlänge des kreisförmigen Integrationsweges. Durch beliebig große Wahl von folgt bereits , und da ein Gebiet ist, ist konstant.[117]
Eine einfache Folgerung des Satzes von Liouville ist der Fundamentalsatz der Algebra. Dieser besagt, dass jedes nicht-konstante Polynom über den komplexen Zahlen eine Nullstelle hat. Im Reellen gilt dies nicht, da zum Beispiel dort nie Null wird. Für den Beweis wird unter der Annahme, ein nicht-konstantes Polynom habe keine Nullstelle, gefolgert, dass eine beschränkte ganze Funktion ist, also konstant. Dies erzeugt dann einen Widerspruch.[13]
Eine Variante des Satzes von Liouville sagt aus, dass jede holomorphe Funktion konstant ist. Dabei bezeichnet die Riemannsche Zahlenkugel.[118] Auch kann die Beschränktheitsbedingung abgeschwächt werden. Gilt stets für eine ganze Funktion , so ist konstant.[119] Der Satz von Liouville kann ferner auf Polynome verallgemeinert werden. Eine Variante von Hadamard kommt lediglich mit dem Realteil der betrachteten Funktion aus. Ist ganz, für die reelle Zahlen und existieren mit
für alle , dann ist ein Polynom dessen Grad nicht übersteigt.[120]
Eine Folgerung des Satzes von Liouville ist, dass das Bild einer nicht konstanten ganzen Funktion stets dicht in ist.[121]
Kleiner Satz von Picard[Bearbeiten | Quelltext bearbeiten]

Der kleine Satz von Picard stellt eine äußerst starke Verschärfung des Satzes von Liouville dar. Er sagt aus, dass jede nicht konstante ganze Funktion bis auf eine mögliche Ausnahme jeden komplexen Wert annehmen muss.[122] Es gilt für eine beliebige ganze Funktion also entweder , oder mit einer Zahl . Dabei kann auf den Fall der einen Ausnahme nicht verzichtet werden, da zum Beispiel die Exponentialfunktion nicht konstant ist und niemals Null wird.
Obwohl der Satz bei weitem stärker ist als der Satz von Liouville, kann letzterer als Zwischenschritt für den Beweis des Kleinen Satzes von Picard verwendet werden.
Kreisscheiben und Ringgebiete[Bearbeiten | Quelltext bearbeiten]
Lemma von Schwarz[Bearbeiten | Quelltext bearbeiten]
Eine nützliche Anwendung des Maximumsprinzips ist der Beweis des Schwarzschen Lemmas: Ist eine holomorphe Selbstabbildung der offenen Einheitskreisscheibe mit der Fixierung des Ursprungs , so gilt für alle und insbesondere .[107]
Eine Verallgemeinerung des Schwarzschen Lemmas ist das Lemma von Schwarz-Pick.[123]
Konvexe Abbildungen, die Pólya-Schoenberg-Vermutung und der Satz von Study[Bearbeiten | Quelltext bearbeiten]
Eine holomorphe Funktion mit und heißt konvex, wenn sie injektiv auf ein konvexes Gebiet abbildet. Ist ihr Bild sogar ein Sterngebiet, so ist starlike („sternartig“). Es ist genau dann konvex, falls entweder starlike ist, oder für alle die Ungleichung
erfüllt ist. Sind and beide konvex, so besagt eine Vermutung von Pólya-Schoenberg, dass auch konvex ist. Diese Vermutung wurde 1973 von Ruscheweyh und Sheil-Small bewiesen.[124] John L. Lewis verwendete sie, um zu zeigen, dass jeder Polylogarithmus für eine konvexe Funktion ist.[125] Keineswegs muss eine starlike-Funktion sämtliche geschlossenen Kurven , die Sterngebiete umschließen, in solche überführen, die ebenfalls Sterngebiete umschließen. Gegenbeispiele stammen von A. W. Goodman. Goodman zeigte jedoch, dass eine starlike Funktion diese Eigenschaft, genannt uniformly starlike, besitzt, genau dann wenn
für alle .[126]
Eine wenig bekannte Anwendung des Schwarzschen Lemmas auf konvexe Funktionen führt zum Satz von Study. Ist biholomorph und das Gebiet konvex, so ist jedes der Gebiete konvex, wobei . Ist zudem ein Sterngebiet mit Zentrum , so ist für alle auch ein Sterngebiet mit Zentrum .[127]
Ist holomorph, mit und , sowie konvex, gilt bereits .[128]
Satz von Bloch[Bearbeiten | Quelltext bearbeiten]
Der Satz von Bloch, bewiesen 1925 von André Bloch, gibt eine Grenze für die Komplexität des Bildgebiets holomorpher Funktionen an.
In der von Bloch gezeigten Version besagt der Satz, dass, wenn die offene Menge die abgeschlossene Einheitskreisscheibe enthält und eine holomorphe Funktion mit den Eigenschaften und ist, es dann eine Kreisscheibe gibt, sodass die Einschränkung injektiv ist und das Bild eine Kreisscheibe mit Radius mindestens enthält.[129]
Man kann zur Verschärfung des Satzes für eine holomorphe Funktion unter obigen Voraussetzungen das Supremum aller Radien definieren, sodass injektiv für eine Kreisscheibe ist und eine Kreisscheibe mit Radius enthält. Bildet man nun das Infimum all dieser Zahlen , wenn die obigen Eigenschaften hat, kann man die Blochsche Konstante definieren durch
Der Satz von Bloch impliziert , aber die Funktion zeigt, dass auch . Es wurde bereits bewiesen, dass
gilt. Dabei bezeichnet die Gammafunktion. Die Abschätzung nach oben stammt von Lars Ahlfors und Helmut Grunsky aus dem Jahr 1937.[130] Beide vermuteten zudem, dass ihre obere Schranke sogar der wahre Wert von ist, was jedoch unbewiesen ist.[131]
Satz von Schottky[Bearbeiten | Quelltext bearbeiten]
Der Satz von Schottky macht eine Aussage über die Werteverteilung einer holomorphen Funktion, die zwei Werte in ihrem Bildbereich auslässt.
Der Satz besagt, dass für alle Werte und eine Konstante existiert, mit folgender Eigenschaft: Ist ein Elementargebiet, das die abgeschlossene Kreisscheibe enthält, und eine beliebige holomorphe Funktion, welche die Werte 0 und 1 nicht annimmt und erfüllt, so gilt für alle .[132]
Daraus kann eine Aussage mit abgeschlossenen Kreisscheiben mit beliebigem Radius gefolgert werden. Enthält das Elementargebiet die Menge und lässt die holomorphe Funktion die Werte 0 und 1 aus, so gilt im Falle für die Konstante aus Schottkys Satz die Abschätzung für alle .[133]
Satz von Koebe[Bearbeiten | Quelltext bearbeiten]
Für holomorphe und injektive Funktionen mit und besagt Satz von Koebe, dass stets .[134]
Volumina von Bildern[Bearbeiten | Quelltext bearbeiten]
Es sei holomorph und injektiv auf dem Kreisrand . Es führe diesen auf eine geschlossene Kurve über. Der Inhalt des durch umschlossenen Gebiets ist dann[135]
Der Inhalt wird positiv oder negativ gerechnet, je nachdem ob bei positivem Umlaufen des Kreises der mitbewegte Bildpunkt das durch umschlossene Gebiet links oder rechts lässt.
Für Kreisringe gilt entsprechend für das Volumen dessen Bildes (mehrfach überdeckte Teile mehrfach gezählt)
Monotonie[Bearbeiten | Quelltext bearbeiten]
Um Beträge holomorpher Funktionen auf Kreislinien auf Monotonie zu untersuchen, ist das Konzept der Folgendifferenzen von Bedeutung. Für reelle Zahlen setzt man , , usw. Es gilt allgemein die Formel
Eine monoton fallende Nullfolge bezeichnet man als -fach monoton, falls für alle und . Ist holomorph auf der Einheitskreisscheibe , konvergiert zudem für und ist vierfach monoton, so ist eine auf dem Intervall fallende Funktion.[136]
Bohr-Radius[Bearbeiten | Quelltext bearbeiten]
Im Jahr 1914 konnte Harald Bohr zeigen, dass falls die Potenzreihe in der Einheitskreisscheibe konvergiert und die holomorphe Funktion in erfüllt, bereits
gilt.[137] Das sogar gilt und der größtmögliche Bohr-Radius ist, konnte unabhängig von Friedrich Wilhelm Wiener, Marcel Riesz und Issai Schur gezeigt werden.
Um wesentliche Singularitäten[Bearbeiten | Quelltext bearbeiten]
Satz von Casorati-Weierstraß[Bearbeiten | Quelltext bearbeiten]

Sei ein Punkt des Gebietes . Dann ist eine wesentliche Singularität der auf holomorphen Funktion genau dann, wenn für jede in liegende Umgebung von das Bild dicht in liegt.
Anders formuliert: Eine holomorphe Funktion hat genau dann in eine wesentliche Singularität, wenn in jeder Umgebung von jede komplexe Zahl beliebig genau als ein Bild von approximiert werden kann.
Großer Satz von Picard[Bearbeiten | Quelltext bearbeiten]
Sei offen und eine wesentliche Singularität der holomorphen Funktion . Der große Satz von Picard besagt, dass dann nur zwei Fälle möglich sind:
- Für jede punktierte Umgebung von gilt .
- Für jede punktierte Umgebung von gilt mit einem geeigneten .
Demnach kommt die Funktion nahe ihrer wesentlichen Singularität nicht nur jedem Wert beliebig nahe, sondern nimmt, bis auf eine mögliche Ausnahme, jeden beliebigen Wert unendlich oft an.[138]
Folgen und Reihen holomorpher Funktionen[Bearbeiten | Quelltext bearbeiten]
Weierstraßscher Konvergenzsatz[Bearbeiten | Quelltext bearbeiten]

Es sei offen und eine Folge auf holomorpher Funktionen. Wird angenommen, dass gleichmäßig auf kompakten Teilmengen gegen eine Funktion konvergiert, so besagt der Satz von Weierstraß, dass die Grenzfunktion wieder holomorph ist und man Limesbildung und Differentiation vertauschen kann. Das heißt, die Folge konvergiert ebenfalls kompakt gegen .[139]
Der Beweis des Satzes ergibt sich unmittelbar aus der Tatsache, dass sich die komplexe Differenzierbarkeit nach dem Satz von Morera durch ein Integralkriterium ausdrücken lässt und dass das betroffene Kurvenintegral stabil unter gleichmäßiger Konvergenz ist. Die Aussage über die Folge ergibt sich aus der Cauchyschen Integralformel.[139]
Der Satz kann weiter verschärft werden. Es sei ein beschränktes Gebiet und eine Folge in holomorpher Funktionen mit stetiger Fortsetzung nach , sodass die Einschränkung auf gleichmäßig konvergiert. Dann konvergiert gleichmäßig gegen eine in holomorphe Funktion, die sich stetig nach fortsetzt.[140]
Die analoge Aussage im Reellen ist falsch. Nach dem Approximationssatz von Weierstraß ist jede stetige Funktion der Grenzwert einer gleichmäßig konvergenten Folge von Polynomen. Allerdings gibt es auch einen Stabilitätssatz im Reellen, der unter Bedingungen an die Folge richtig ist.[139]
Unendliche Reihen[Bearbeiten | Quelltext bearbeiten]
Der Satz von Weierstraß lässt sich auf unendliche Reihen anwenden. Ist eine Folge holomorpher Funktionen, so konvergiert gegen eine holomorphe Funktion , falls sie in normal konvergiert, d. h. für jeden Punkt gibt es eine Umgebung , so dass[141]
Integralfolgen[Bearbeiten | Quelltext bearbeiten]
Einige holomorphe Funktionen treten als Integrale in Erscheinung. Es gilt dabei Folgendes. Es sei , eine stetige komplexwertige Funktion auf , wobei eine offene Menge bezeichnet. Ferner sei für jedes fixierte eine holomorphe Funktion. Dann ist die Funktion
holomorph in .[142] In Kombination mit dem Weierstraßschen Konvergenzsatz können damit auch Integrale mit unendlichen Grenzen behandelt werden. Ein wichtiges Beispiel ist die Gammafunktion. Die Integrale
stellen nach eben genanntem Kriterium eine Funktionenfolge holomorpher Funktionen dar. Es lässt sich zeigen, dass auf Kompakta in gleichmäßige Konvergenz für vorliegt. Damit ist die Grenzfunktion
eine in ganz holomorphe Funktion.[143]
Satz von Hurwitz[Bearbeiten | Quelltext bearbeiten]

Der Satz von Hurwitz trifft eine Aussage über das lokale Nullstellenverhalten einer holomorphen Funktionenfolge, deren Grenzfunktion wieder holomorph ist.
Sei ein Gebiet und eine Folge holomorpher Funktionen mit nicht konstanter holomorpher Grenzfunktion . Es gelte zudem für ein . Dann gibt es zu jeder Kreisscheibe ein , sodass jede der Funktionen mit eine Nullstelle in hat.[144]
Mit anderen Worten, konvergiert eine Folge auf einem Gebiet holomorpher Funktionen gegen eine holomorphe Grenzfunktion mit Nullstelle, so werden fast alle Folgeglieder beliebig nahe an der Nullstelle verschwinden.[144]
Eine wichtige Folgerung des Satzes von Hurwitz betrifft Folgen injektiver holomorpher Funktionen. Besteht die konvergente Folge aus injektiven holomorphen Funktionen und ist die holomorphe Grenzfunktion nicht konstant, so ist diese wieder injektiv.[145] Diese Aussage kann in einem gewissen Sinn umgekehrt werden: Konvergieren die holomorphen Funktionen lokal gleichmäßig gegen eine injektive (holomorphe) Funktion , so existiert zu jedem Kompaktum ein Index , so dass für alle die Einschränkungen injektiv sind.[146]
Beachtenswert ist, dass in manchen Fällen sogar die Stetigkeit der Folgeglieder ausreicht, um etwas über das Bild der Grenzfunktion zu sagen. Ist ein Gebiet und eine Folge stetiger Funktionen , die lokal gleichmäßig gegen eine auf holomorphe Grenzfunktion konvergieren. Dann ist entweder konstant oder .[147]
Satz von Montel[Bearbeiten | Quelltext bearbeiten]
Ist eine Folge holomorpher Funktionen auf lokal beschränkt, so existiert eine kompakt konvergente Teilfolge. Der Beweis dieses Satzes wird mit Hilfe des Satzes von Bolzano-Weierstraß geführt und beim Beweis des Riemannschen Abbildungssatzes verwendet.[148]
Dienlich für den Beweis ist ebenfalls folgender Hilfssatz. Ist eine beschränkte Folge auf holomorpher Funktionen, die auf einer dichten Teilmenge punktweise konvergiert, so konvergiert sie sogar in ganz , und zwar lokal gleichmäßig.[149]
Punktweise konvergente Folgen[Bearbeiten | Quelltext bearbeiten]
Satz von Vitali[Bearbeiten | Quelltext bearbeiten]

Folgende Aussagen über eine im Gebiet lokal beschränkte Folge holomorpher Funktionen sind äquivalent:[150]
- Die Folge ist in kompakt konvergent.
- Es existiert ein Punkt , sodass für alle die Zahlenfolge konvergiert.
- Die Menge der Konvergenzpunkte hat einen Häufungspunkt in .
Gewisse Informationen über die Nullstellen der Folgeglieder bringen ebenfalls starke Vorteile mit sich, denn sie erlauben es dass punktweise Konvergenz in nur einem Punkt ausreicht. Ist ein Gebiet und eine Folge holomorpher, lokal gleichmäßig beschränkter und nullstellenfreier Funktionen auf , so folgt aus mit einem bereits in mit lokal gleichmäßiger Konvergenz.[151]
Die Frage, ob im Satz von Vitali die Voraussetzung der lokalen Beschränktheit durch punktweise Konvergenz in allen Punkten ersetzt werden kann, kann negativ beantwortet werden. Gegenbeispiele liegen alles andere als auf der Hand, können aber zum Beispiel durch Runge-Theorie erzeugt werden.[152] Jedoch zeigte William Fogg Osgood, dass im Falle punktweiser Konvergenz in allen Punkten ohne weitere Voraussetzungen zumindest Holomorphie der Grenzfunktion auf einer dichten Teilmenge des Gebietes vorliegen muss. Ist also eine Folge holomorpher Funktionen auf einem Gebiet , die punktweise gegen eine Grenzfunktion konvergiert, so ist auf einer dichten, offenen Teilmenge kompakt konvergent. Insbesondere ist die Grenzfunktion holomorph auf .[153] Für den Fall, dass die Funktionen zusätzlich injektiv sind, liegt bei lediglich punktweiser Konvergenz jedoch wieder Holomorphie der Grenzfunktion im gesamten Gebiet vor.[154]
Satz von Blaschke[Bearbeiten | Quelltext bearbeiten]
Unter gewissen Zusatzvoraussetzungen ist punktweise Konvergenz, sogar nur an bestimmten Stellen, wieder hinreichend für eine holomorphe Grenzfunktion. Der Satz von Blaschke aus dem Jahr 1915 besagt, dass falls eine gleichmäßig beschränkte holomorphe Funktionenfolge auf dem Einheitskreis ist und eine Folge paarweise verschiedener Punkte in mit
so dass für jedes existiert, gleichmäßig auf Kompakta in konvergiert, und die Grenzfunktion insbesondere holomorph ist.[155]
Satz von Carathéodory-Landau[Bearbeiten | Quelltext bearbeiten]
Es seien mit und eine Folge holomorpher Funktionen . Es existiere für eine Menge von Punkten in , die in einen Häufungspunkt hat. Dann konvergiert die Folge kompakt in , hat also eine holomorphe Grenzfunktion.[156]
Zusammenhang mit harmonischen Funktionen[Bearbeiten | Quelltext bearbeiten]
Eine auf einem Gebiet zweimal stetig partiell differenzierbare Funktion mit der Eigenschaft
auf ganz nennt man harmonisch. Es ist der sogenannte Laplace-Operator in Dimension 2, und alternativ gilt die Kurzschreibweise . Zwischen harmonischen Funktionen und holomorphen Funktionen existieren enge Verbindungen. Aufgrund der Tatsache, dass Real- und Imaginärteil einer holomorphen Funktion die Cauchy-Riemannschen Differentialgleichungen erfüllen, kann man etwa zeigen, dass diese bereits harmonische Funktionen sind.[157] Es gilt lokal sogar die Umkehrung: Zu jeder auf einem Elementargebiet harmonischen Funktion gibt es eine dort holomorphe Funktion , die diese als Realteil hat. Dies sieht man erneut mit Hilfe der Cauchy-Riemannschen Differentialgleichungen: Es ist die Hilfsfunktion holomorph. Da der Definitionsbereich ein Elementargebiet ist, existiert zu eine holomorphe Stammfunktion, deren Realteil bis auf eine Konstante mit übereinstimmt.[158] Die in zum Realteil zugehörige harmonische Funktion wird als konjugiert harmonisch zu bezeichnet. Sie ist bis auf eine additive Konstante eindeutig bestimmt.[159]
Konstruktion, Approximation und Existenzaussagen[Bearbeiten | Quelltext bearbeiten]
Produktsatz von Weierstraß[Bearbeiten | Quelltext bearbeiten]
Es kann gefragt werden, ob es zu einer gegebenen Nullstellenverteilung eine ganze Funktion gibt, die diese erfüllt. So erfüllt etwa die Nullstellenverteilung . Der Produktsatz von Weierstraß, bewiesen 1876, beantwortet diese Frage. Ist eine diskrete Teilmenge, und es sei eine Abbildung mit gegeben, dann existiert eine ganze Funktion mit folgenden Eigenschaften:[160]
- für alle .
Mit anderen Worten gibt es zu jeder diskreten Menge und jeder „Gewichtung“ der Punkte durch natürliche Zahlen eine ganze Funktion , die ihre Nullstellen genau an den Stellen hat und deren Vielfachheit auch der entsprechenden Gewichtung entspricht.
Ein bedeutendes Beispiel ist das bereits von Leonhard Euler im Jahr 1734 entdeckte Sinus-Produkt
das in ganz konvergiert.[161]
Der Produktsatz kann auf beliebige Gebiete ausgeweitet werden. Ist ein Gebiet, eine Folge paarweise verschiedener Punkte in , die sich in nicht häuft, sowie eine Folge positiver ganzer Zahlen, so gibt es stets eine holomorphe Funktion , die ihre Nullstellen genau in den hat, wobei die Ordnung von genau ist.[162] Eine wichtige Folgerung dieser Tatsache ist, dass sich jede meromorphe Funktion als Quotient zweier auf holomorpher Funktionen schreiben lässt.[163]
Satz von Mittag-Leffler[Bearbeiten | Quelltext bearbeiten]

Es sei eine diskrete Menge. Der Satz von Mittag-Leffler garantiert die Existenz einer auf ganz holomorphen Funktion, die bestimmte Laurent-Entwicklungen an den Stellen hat. Ist präzise zu jedem eine ganze Funktion vorgegeben mit , so gibt es eine holomorphe Funktion , deren Hauptteil in gegeben ist durch , d. h.,
hat in eine hebbare Singularität. Ist endlich, so ist
eine Lösung des Mittag-Leffler-Problems. Für unendliche wird eine solche Reihe aber im Allgemeinen nicht mehr konvergieren. Ähnlich wie beim Produktsatz von Weierstraß kann hier jedoch mit konvergenzerzeugenden Summanden Konvergenz erzwungen werden.[164]
Satz von Runge[Bearbeiten | Quelltext bearbeiten]
Der Satz von Taylor besagt, dass sich holomorphe Funktionen innerhalb von Kreisscheiben gleichmäßig auf Kompakta durch Polynome approximieren lassen. Der Satz von Runge verallgemeinert dieses Resultat auf beliebige kompakte Teilmengen, wobei die Annäherung zumindest über rationale Funktionen gelingt. Ist eine kompakte Teilmenge und eine Funktion, die holomorph in einer offenen Menge ist, die vollständig beinhaltet, so ist es möglich, innerhalb von gleichmäßig durch rationale Funktionen zu approximieren. Dabei liegen alle Polstellen der außerhalb von .[165]
Der Satz von Runge existiert auch in einer Version für Polynome. Sei offen. Dann ist der Zusammenhang des Komplements (mit der auf der Riemannschen Zahlenkugel üblichen Topologie) notwendig und hinreichend für die folgende Aussage: Für jede auf holomorphe Funktion , für jedes und für jede kompakte Teilmenge gibt es ein Polynom , so dass
für alle .[166]
Partialbruchzerlegungen[Bearbeiten | Quelltext bearbeiten]
Ist eine ganze Funktion, die für Konstanten stets die Ungleichung
erfüllt, so gilt bereits[167]
Ist zusätzlich eine ungerade Funktion, ist also stets , gilt
Für führt dies, nach einem Shift im Argument, zur Partialbruchzerlegung des Kotangens.
Eine Quelle von Partialbruchzerlegungen sind logarithmisch abgeleitete Weierstraß- oder auch Hadamard-Produkte. Sie können auch zu einer Approximation dienen: Sei eine holomoorphe Funktion in der geschlossenen Kreisscheibe mit , so dass für alle . Es sei die Liste der Nullstellen von (gezählt mit Vielfachheit), in der Kreisscheibe . Dann gilt für alle mit [168]
Interpolation[Bearbeiten | Quelltext bearbeiten]
Es seien beliebige voneinander verschiedene komplexe Zahlen, eine geschlossene, injektive stetige Kurve, die sämtliche Punkte im Innern enthält. Die Funktion sei holomorph im Innern von und auf . Setzt man , so stellt
das eindeutige Polynom -ten Grades dar, das an den Stellen mit übereinstimmt.[169] Dabei wird die Integrationskurve wie üblich einmalig in mathematisch positiver Richtung durchlaufen.
Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Cauchysche Ungleichung[Bearbeiten | Quelltext bearbeiten]
Ist eine Potenzreihe mit Konvergenzradius , und definiert man für ein mit die Konstante , so gilt für die Koeffizienten die Abschätzung
Dies ist eine unmittelbare Folgerung aus der Cauchyschen Integralformel.[170] Diese Aussage lässt sich zu einem Abschätzungsprinzip für Ableitungen auf kompakten Mengen erweitern. Ist offen und ein Kompaktum, dann gibt es zu jeder kompakten Umgebung (es existiert um jedes eine Umgebung, die ganz in liegt) und zu jedem eine Konstante , sodass
- für alle .
Hierbei ist die Supremumsnorm. Es ist zu beachten, dass nicht gewählt werden darf, wie das Beispiel sowie zeigt.[170]
Es kann der Fall für beliebige Ableitungen explizit gemacht werden, und zwar für beliebige Punkte innerhalb von Kreisscheiben. Ist holomorph und beschränkt, also existiert, so gilt für alle und :[171]
Die Cauchysche Ungleichung zeigt, dass das Wachstum der Taylor-Koeffizienten nicht beliebig starke Züge annehmen kann. So existiert etwa keine lokal um 0 holomorphe Funktion mit der Eigenschaft
- .
Im Gegensatz dazu existiert zu jeder reellen Folge eine unendlich oft differenzierbare reelle Funktion mit für alle .[52]
Borel-Carathéodory-Lemma[Bearbeiten | Quelltext bearbeiten]
Sei eine auf einem Gebiet holomorphe Funktion, sodass , und
Dann gilt
und
für und .[172]
Gutzmersche Ungleichung[Bearbeiten | Quelltext bearbeiten]
Ist eine in einer Umgebung von holomorphe Funktion mit Potenzreihe mit dem Konvergenzradius , dann gilt für jedes mit die Ungleichung
Die Ungleichung geht auf August Gutzmer aus dem Jahr 1888 zurück.[173]
Differenzenquotient[Bearbeiten | Quelltext bearbeiten]
Sei eine in holomorphe Funktion und mit . Dann gilt gleichmäßig für alle aus [174]
Dies folgt aus der Standardabschätzung für Integrale:
Dabei wurde im letzten Schritt das Maximumprinzip verwendet. Die Konstante kann im Allgemeinen nicht verbessert werden, wie das Beispiel aufzeigt. Der letzte Schritt kann jedoch auch unter Verzicht der Gleichmäßigkeit weggelassen werden. Mehr noch, ist die Funktion (nur) in einer Umgebung von holomorph, so gilt immer noch
Fejér-Riesz- und Hilbert-Ungleichung[Bearbeiten | Quelltext bearbeiten]
Ist auf der abgeschlossenen Einheitskreisscheibe holomorph, so gilt bereits
Dies bleibt auch dann gültig, wenn lediglich im Hardy-Raum liegt. Insbesondere gilt dann , und die Hilbert-Ungleichung[175]
Grunsky-Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Es sei eine injektive holomorphe Funktion auf der offenen Einheitskreisscheibe, mit sowie . Definiere
Diese besitzt eine Laurent-Entwicklung um :
die für konvergiert. Nun definiert man Zahlen durch
Dann sagen die starken Grunsky-Ungleichungen, dass für jede endliche Folge komplexer Zahlen
Die schwachen Grunsky-Ungleichungen besagen ferner, dass
gilt.[176]
Lebedev–Milin-Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Ist eine holomorphe Funktion auf einer Kreisscheibe mit . Dann ist die Verkettung mit der Exponentialfunktion wieder holomorph auf und hat dort eine Potenzreihenentwicklung
Nun gelten die drei Lebedev–Milin Ungleichungen:[177]
1. Falls , dann
wobei Gleichheit genau dann gilt falls für alle mit einem komplexen .
2. Für gilt
wobei Gleichheit genau dann gilt falls für alle mit einem komplexen .
3. Für gilt
wobei Gleichheit genau dann gilt falls für alle mit einem komplexen .
Kriterien für Konstanz[Bearbeiten | Quelltext bearbeiten]
Durch ihre starken Eigenschaften sind holomorphe Funktionen auf gewisse Weise „selten“. Dementsprechend können einige Kriterien erarbeitet werden, um zu erzwingen, dass eine holomorphe Funktion bereits konstant sein muss.
Klassische Kriterien[Bearbeiten | Quelltext bearbeiten]
Beschränkte ganze Funktionen sind nach dem Satz von Liouville konstant. Mehr noch, lässt eine ganze Funktion zwei Werte in ihrem Bildbereich aus, so ist sie nach dem kleinen Satz von Picard bereits konstant.
Bildet zudem eine holomorphe Funktion eine offene Teilmenge ihres zusammenhängenden Definitionsbereichs nicht auf ein Gebiet ab, ist sie konstant. Sind entsprechend , bzw. konstant, so auch .
Wachstum und Nullstellen[Bearbeiten | Quelltext bearbeiten]
Es sei eine auf der abgeschlossenen oberen Halbebene holomorphe Funktion mit folgenden Eigenschaften:
- Es existieren zwei Konstanten mit für alle mit .
- Es existieren zwei Konstanten , so dass für alle .
- Es gilt für alle .
Dann gilt bereits . In diesem Sinne ist die „kleinste“ holomorphe Funktion, die an (nichtnegativen) ganzen Werten verschwindet.[178] Unter Weglassen von Bedingung 3. kann, wenn 2. zu für abgewandelt wird, ebenfalls gefolgert werden.[179]
Verhalten am Rand der Einheitskreisscheibe[Bearbeiten | Quelltext bearbeiten]
Ist eine auf der Einheitskreisscheibe holomorphe Funktion, so dass für alle :
Ist ferner kein singulärer Punkt von , so ist bereits .[180] Die Annahme, dass kein singulärer Punkt ist, kann durch
ersetzt werden.[181]
Obere Halbebene[Bearbeiten | Quelltext bearbeiten]
Invarianten[Bearbeiten | Quelltext bearbeiten]
Es besitze eine holomorphe Funktion auf der oberen Halbebene die folgenden Eigenschaften:
- Es gilt für alle ,
- Es gilt für alle ,
- Es ist auf beschränkt.
Dann ist bereits konstant.[182] Diese Aussage kann unter Zuhilfenahme des Maximumprinzips und der Tatsache, dass die Gruppe durch Möbiustransformation auf der oberen Halbebene operiert, erhalten werden. Allgemeiner folgt sie aus der Theorie der Modulformen bzw. der Theorie kompakter Riemannscher Flächen.
Anwendungen der oberen Aussage betreffen analytische Beweise des Zwei-Quadrate-Satz und Vier-Quadrate-Satz.[183]
Lage von Nullstellen[Bearbeiten | Quelltext bearbeiten]
Es sei eine auf der oberen Halbebene holomorphe Funktion, die folgende Eigenschaften erfüllt:
- Es ist , wobei mit und .
- Es ist beschränkt.
Dann ist bereits .[184]
Weitere Eigenschaften ganzer Funktionen[Bearbeiten | Quelltext bearbeiten]
Ordnung einer ganzen Funktion[Bearbeiten | Quelltext bearbeiten]
Die Ordnung (im Sinne einer „Wachstumsordnung“) einer ganzen Funktion, falls existent, ist definiert durch die reelle Zahl mit[185]
Es gibt Funktionen endlicher Ordnung, die nicht verschwinden, zum Beispiel usw. In gewissem Sinne sind dies bereits die allgemeinsten Beispiele, denn hat keine Nullstelle, so ist wieder ganz und es gilt mit einem . Demnach ist jede ganze Funktion ohne Nullstelle und endlicher Ordnung bereits von der Form mit einem Polynom .[186]
Ein Wachstumsgesetz kann auch an den Koeffizienten der Taylorreihe abgelesen werden. Gilt und
- ,
so gilt bereits, dass global durch eine von und abhängige Konstante beschränkt ist. Setzt man im Falle ferner für jedes , so folgt[187]
- .
Produktsatz von Hadamard[Bearbeiten | Quelltext bearbeiten]

Der Produktsatz von Hadamard stellt eine Verschärfung des Produktsatzes von Weierstraß für den Fall ganzer Funktionen mit endlicher Ordnung dar. Es bezeichnen die Nullstellen von in aufsteigender Betragsgröße sortiert, wobei . Man definiert und für
Ist nun die kleinste ganze Zahl mit , so gibt es ein Polynom vom Grade höchstens , sodass
Dabei ist die Nullstellenordnung von in 0. Das Produkt erstreckt sich im Falle endlich vieler Nullstellen nur über endlich viele Werte.[188]
Approximation stetiger Funktionen[Bearbeiten | Quelltext bearbeiten]
Die Reichhaltigkeit der Menge der ganzen Funktionen im Gegensatz zum Polynomring wird unter anderem durch folgenden Satz von Torsten Carleman aus dem Jahr 1927 deutlich: Sei eine stetige Funktion („Fehlerfunktion“). Dann gibt es zu jeder stetigen Funktion eine ganze Funktion , sodass für alle gilt[189]
Für eine solche Approximationsstärke reicht die Auswahl an Polynomen nicht aus. So ist etwa die reelle Funktion keinesfalls auf ganz durch Polynome mit Güte einer beliebigen Fehlerfunktion approximierbar. Nach einem Satz von Weierstraß ist dies jedoch auf kompakten Intervallen sehr wohl möglich.[189]
Transzendente Funktionen[Bearbeiten | Quelltext bearbeiten]
Für den Fall endlicher Ordnung ist die Menge der rationalen Stellen, die zwei algebraisch unabhängige ganze Funktionen annehmen können, limitiert. Es bezeichnen ganze Funktionen mit der Eigenschaft für ein (im englischen strict order ). Dabei sind mindestens zwei hiervon algebraisch unabhängig (also gehen nicht durch die vier Grundrechenarten auseinander hervor). Zudem wird verlangt, dass der Ring bezüglich des Differentialoperators sich selbst abbildet, es gibt also stets ein Polynom mit rationalen Koeffizienten, sodass
Sind nun paarweise verschiedene komplexe Zahlen mit für und , gilt bereits .[190] Eine klassische Anwendung dieses Satzes betrifft den Ring , der unter abgeschlossen ist. Dann besagt der Satz, dass keiner der Werte mit ganzen Zahlen rational sein kann, da es sonst alle Werte wären. Analoge Resultate existieren für den Fall algebraischer und nicht bloß rationaler Zahlen.[191] Eine wichtige Anwendung dieser Theorie ist der Satz von Gelfond-Schneider.[190]
Analytische Fortsetzung[Bearbeiten | Quelltext bearbeiten]
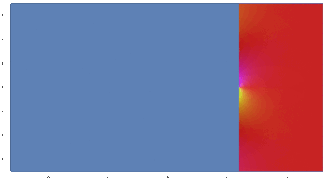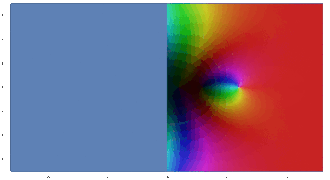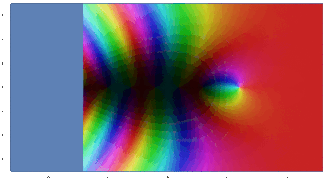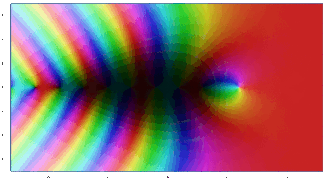
Ist in einem Gebiet holomorph und entwickelt man um einen Punkt in seine Taylor-Reihe, so ist deren Konvergenzradius mindestens gleich dem Abstand von zum Rand von , er kann jedoch auch größer sein. In diesem Fall sagt man, dass über hinaus „analytisch fortgesetzt“ ist.[192]
Fortsetzung reeller Funktionen[Bearbeiten | Quelltext bearbeiten]
Ist eine reelle Funktion auf einem echten Intervall , so besitzt genau dann eine analytische Fortsetzung auf ein Gebiet , falls reell-analytisch ist.[193]
Eindeutigkeit der analytischen Fortsetzung[Bearbeiten | Quelltext bearbeiten]
Sei ein Gebiet, eine Menge mit mindestens einem Häufungspunkt in und eine Funktion. Wenn eine holomorphe Funktion existiert, die fortsetzt, d. h. , so ist diese eindeutig bestimmt. Dieses Resultat ist eine einfache, aber sehr wichtige Folgerung des Identitätssatzes für holomorphe Funktionen.[101] Ist zum Beispiel , sowie , so besagt es, dass die Exponentialfunktion nur eine einzige Fortsetzung zu einer in ganz holomorphen Funktion besitzt. Es gilt dann
Monodromiesatz[Bearbeiten | Quelltext bearbeiten]

Ein wichtiger Ansatz, eine zunächst lokal holomorphe Funktion auf größere Bereiche fortzusetzen, ist das Prinzip der analytischen Fortsetzung entlang einer Kurve. Ist holomorph in einem Punkt , so kann sie dort in eine Taylor-Reihe entwickelt werden. Geht man nun vom Entwicklungspunkt weg, können am Rande des Konvergenzbereichs alle Ableitungen von bestimmt werden, womit eine erneute Taylor-Entwicklung möglich wird, deren Konvergenzbereich eventuell aus dem Bereich der ursprünglichen Entwicklung hinausreicht. Verfährt man so fort, kann eventuell entlang eines Weges bis zu einem Punkt , der möglicherweise weit weg von liegt, fortgesetzt werden. Der Monodromiesatz besagt, dass wenn und durch zwei Wege und verbunden sind, die durch eine Abbildung mit stetig ineinander übergeführt werden können, sodass sich entlang jeden der Wege analytisch fortsetzen lässt, dass dann die Fortsetzungen und von entlang und in beide übereinstimmen.[194]
Schwarzsches Spiegelungsprinzip[Bearbeiten | Quelltext bearbeiten]
Das Schwarzsche Spiegelungsprinzip erlaubt unter gewissen Symmetrievoraussetzungen eine analytische Fortsetzung. Sei ein zu symmetrisches Gebiet, das heißt , und man setze
- , sowie .
Dann gilt: Ist stetig, holomorph und , dann ist die durch
definierte Funktion holomorph. Dabei bezeichnet die komplexe Konjugation.[195]
Holomorphiegebiete[Bearbeiten | Quelltext bearbeiten]
Ein Gebiet heißt das Holomorphiegebiet einer in holomorphen Funktion , wenn für jeden Punkt die Konvergenzkreisscheibe der Taylorreihe von um in liegt. Dann folgt sofort: Ist das Holomorphiegebiet von , so ist das „maximale Existenzgebiet“ von , d. h. jedes Gebiet , in dem es eine Funktion mit gibt, stimmt mit überein.[57] Es kann eine (auf einem Gebiet) holomorphe Funktion also niemals über ihr Holomorphiegebiet hinaus analytisch fortgesetzt werden. Im Allgemeinen besagt Holomorphiegebiet aber mehr als maximales Existenzgebiet. Die geschlitzte Ebene ist z. B. das maximale Existenzgebiet der dort holomorphen Funktionen und , jedoch nicht deren Holomorphiegebiet: die Taylor-Reihen von und um haben als Konvergenzkreis, und es gilt , falls . Die Funktionen und sind „von oben und unten“ in jedem Punkt auf der negativen reellen Achse holomorph fortsetzbar, alle Randpunkte in sind aber „singulär“ für und in dem Sinne, dass keiner eine Umgebung mit einer Funktion hat, die in mit bzw. übereinstimmt.[196]
Es sind die Gebiete , bzw. die Holomorphiegebiete der Funktionen , bzw.
- .
Der Existenzsatz für Holomorphiegebiete besagt, dass jedes Gebiet das Holomorphiegebiet irgendeiner dort holomorphen Funktion ist.[197]
Biholomorphe und schlichte Funktionen[Bearbeiten | Quelltext bearbeiten]
Eine Funktion, die holomorph, bijektiv und deren Umkehrfunktion holomorph ist, nennt man biholomorph. In der Literatur wird statt biholomorph gelegentlich auch der Begriff konform verwendet.[198] Aus dem Satz über implizite Funktionen folgt für holomorphe Funktionen einer Veränderlicher schon, dass eine bijektive, holomorphe Funktion stets eine holomorphe Umkehrabbildung besitzt.[198]
Auch im Fall mehrerer Veränderlicher garantiert der Satz von Osgood die Eigenschaft, dass Bijektivität und Holomorphie automatisch Holomorphie der Umkehrabbildung impliziert. Somit kann man sagen, dass bijektive, holomorphe Abbildungen biholomorph sind.
Inverse Funktion[Bearbeiten | Quelltext bearbeiten]
Ist eine holomorphe Funktion und gilt für ein , so ist dort lokal biholomorph. Das heißt, dass es eine Umgebung gibt, sodass die Einschränkung biholomorph ist.[199] Zu beachten ist die Lokalität der Biholomorphie. So verschwindet die Ableitung der komplexen Exponentialfunktion – sie selbst – an keiner Stelle, jedoch ist sie nicht injektiv, da zum Beispiel . Andersherum verschwindet die Ableitung einer injektiven holomorphen Funktion an keiner Stelle ihres Definitionsbereichs.[200] Trotz dieser Restriktion kann manchmal in einem gewissen Sinne nach unten hin quantifiziert werden, welche Kreisscheiben lokal injektiv abgebildet werden. Ist holomorph auf , und , sowie
existent, bildet die Kreisscheibe biholomorph auf eine Menge ab, welche die Scheibe enthält.[201]
Für die Umkehrfunktion einer biholomorphen Funktion kann mittels des Residuensatzes eine lokal gültige Darstellung hergeleitet werden. Ist ein Gebiet, biholomorph und eine abgeschlossene Kreisscheibe, dann gilt für alle die Formel:[202]
Dieser Ansatz kann verwendet werden, um Potenzreihen lokal umzukehren. Besitzt die biholomorphe Funktion – ohne Einschränkung der Allgemeinheit gelte – um die lokale Entwicklung
- mit ,
so geben Philip M. Morse und Herman Feshbach die folgende Reihe für die Umkehrfunktion an:[203]
mit
Dabei bezeichnet das Symbol die Fakultät. Die ersten Werte sind[204]
- , , und .
Die lokale Umkehrung von Potenzreihen ist auch Gegenstand der Lagrangeschen Inversionsformel.
Riemannscher Abbildungssatz[Bearbeiten | Quelltext bearbeiten]

Eine Klassifikation aller Elementargebiete liefert der Riemannsche Abbildungssatz. Dieser sagt aus, dass zwischen zwei Elementargebieten, die beide nicht ganz umfassen, stets eine biholomorphe Abbildung existiert. Somit ist jedes Elementargebiet, das nicht ganz ist, zur Einheitskreisscheibe biholomorph äquivalent.[205] Es gibt daher aus der Sicht analytischer Abbildungen nur „zwei Typen“ von Elementargebieten, nämlich und . Es ist aber zu beachten, dass und als topologische Räume homöomorph sind über die nichtholomorphe Abbildung mit[205][206]
In einer Verallgemeinerung sagt der Riemannsche Abbildungssatz, dass jedes Elementargebiet in biholomorph äquivalent entweder zu , oder ganz ist.
Theorem von Carathéodory[Bearbeiten | Quelltext bearbeiten]
Über das sog. Fortsetzungslemma kann eine Randaussage von auf dem Einheitskreis definierten biholomorphen Funktionen in ein Gebiet getroffen werden. Es kann genau dann zu einer in ganz stetigen Funktion nach fortgesetzt werden, wenn der Rand von ein geschlossener Weg ist, d. h., es gibt eine stetige Abbildung mit . Constantin Carathéodory konnte diese Aussage präzisieren: Es lässt sich genau dann zu einem Homöomorphismus von nach fortsetzen, wenn eine geschlossene Jordan-Kurve ist, also den Rand von homöomorph auf den Rand von abbildet.[207]
Automorphismen[Bearbeiten | Quelltext bearbeiten]
Bei Automorphismengruppen handelt es sich im Kontext holomorpher Funktionen um Kollektionen biholomorpher Selbstabbildungen. Für eine offene Menge bezeichnet die Menge aller biholomorphen Abbildungen .[208] Die Verknüpfung der Gruppe ist hierbei durch Verkettung gegeben. Beispielsweise enthält die Gruppe als Elemente alle biholomorphen ganzen Funktionen.
Die Automorphismengruppe eines Gebietes enthält wichtige Informationen über dessen Funktionentheorie. So können zwei Gebiete nur dann biholomorph äquivalent sein, wenn ihre Automorphismengruppen isomorph sind.[209]
Komplexe Zahlenebene[Bearbeiten | Quelltext bearbeiten]
Jeder Automorphismus von entspricht einer nichtkonstanten affin-linearen Abbildung, hat also die Form mit . Umgekehrt ist jede solche Funktion ein Automorphismus.[210] Damit gilt
Der Beweis zur Klassifikation benutzt die Tatsache, dass jeder Automorphismus eine ganze Funktion sein muss, aber in keine wesentliche Singularität haben kann, da andernfalls nach dem Satz von Casorati-Weierstraß die Umkehrfunktion nicht stetig in wäre (alternativ kann man mit dem großen Satz von Picard direkt zeigen, dass nicht injektiv sein kann). Somit besitzt einen Pol in und ist ein Polynom, das Grad 1 haben muss, da jedes höhere Polynom nach dem Fundamentalsatz der Algebra als ganze Funktion nicht injektiv ist.[210]
Gelochte Zahlenebene[Bearbeiten | Quelltext bearbeiten]
Setzt man , so gilt
Die Gruppe ist nicht abelsch: Sie zerfällt in zwei zu isomorphe Zusammenhangskomponenten.[211]
Einheitskreisscheibe[Bearbeiten | Quelltext bearbeiten]
Die Automorphismengruppe der Einheitskreisscheibe hat die Gestalt[212]
Betrachtet man die Untergruppe aller Abbildungen mit der Eigenschaft , so ergibt sich, dass diese genau von der Form mit einem sind. Es handelt sich also genau um alle Drehungen. Diese Aussage kann als Vorbereitung zur Bestimmung von ganz dienen.[213]
Gelochte Einheitskreisscheibe[Bearbeiten | Quelltext bearbeiten]
Für gilt
- .
Damit ist zur Kreisgruppe isomorph.[214]
Obere Halbebene[Bearbeiten | Quelltext bearbeiten]
Obwohl die obere Halbebene der komplexen Zahlen biholomorph äquivalent zur Einheitskreisscheibe ist, nämlich über die Abbildung ,[215] ist es von Interesse, ihre Automorphismengruppe separat anzugeben. Grund hierfür ist der Zusammenhang zur hyperbolischen Geometrie sowie zur Theorie der Modulfunktionen.
Die Automorphismengruppe ist
Jedes korrespondiert also zu einer Matrix
und für zwei gilt genau dann, wenn für die zugehörigen Matrizen und gilt .[216] Dabei bezeichnet die spezielle lineare Gruppe der reellen -Matrizen. Ferner sind sogar die Gruppen und zueinander isomorph vermöge .[217][218] Dabei bezeichnet die -Einheitsmatrix.
Starre Gebiete[Bearbeiten | Quelltext bearbeiten]
Bei starren Gebieten handelt es sich um Gebiete mit der Eigenschaft .[214] Die Gruppe der Automorphismen von ist also trivial. Beispiel eines starren Gebietes ist .[219]
Asymptotische Analysis holomorpher Funktionen[Bearbeiten | Quelltext bearbeiten]
Definitionen und elementare Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Eine formale Potenzreihe heißt asymptotische Entwicklung einer holomorphen Funktion auf einem Gebiet mit , falls für alle gilt
So ein hat stets höchstens eine asymptotische Entwicklung. Die Existenz einer asymptotischen Entwicklung hängt empfindlich von der Art des Gebietes ab. So besitzt die Funktion für keine asymptotische Entwicklung, jedoch für jeden Kreissektor mit Hat eine holomorphe Fortsetzung in ein Gebiet mit , so entspricht die asymptotische Entwicklung der Funktion der Taylorentwicklung von um 0.[220]
Ist holomorph und für gleichmäßig auf einem Kreissektor , so folgt bereits
auf .[221] Dabei bedeutet gleichmäßig, dass
für in und , wobei die -Konstante aber nicht von der Wahl des Weges von abhängt.
Existenz asymptotischer Entwicklungen[Bearbeiten | Quelltext bearbeiten]
Folgendes Kriterium ist für die Existenz asymptotischer Entwicklungen hinreichend. Sei ein Gebiet mit , sodass es zu jedem Punkt eine Nullfolge gibt mit der Eigenschaft, dass jede Strecke in liegt. Ist dann eine in holomorphe Funktion, für die alle Limites existieren, so hat die asymptotische Entwicklung[222]
Zu beachten ist, dass die an gestellten Voraussetzungen für alle Kreissektoren um 0 erfüllt sind.[223]
Satz von Ritt[Bearbeiten | Quelltext bearbeiten]
Die Frage, welche Bedingungen Potenzreihen erfüllen müssen, um als asymptotische Entwicklung holomorpher Funktionen aufzutreten, hat für Kreissektoren um 0 eine einfache Antwort: Es gibt keine solchen Bedingungen.[224] Genauer gilt der Satz von Ritt: Ist ein echter Kreissektor um 0, so existiert zu jeder formalen Potenzreihe eine in holomorphe Funktion , sodass gilt:[225]
Summenformeln[Bearbeiten | Quelltext bearbeiten]
In manchen Anwendungen ist es vonnöten, Summen der Gestalt für (in einem Winkelbereich) zu verstehen. Erfüllt gewisse Eigenschaften, darunter Holomorphie, kann dies bewerkstelligt werden. Im Folgenden sei stets mit einem .
Es sei nun eine Funktion, die in einer Umgebung von holomorph ist, insbesondere im Ursprung. Ferner gebe es für jedes ein , so dass wenn in . Dann gilt für alle und :
gleichmäßig, sofern in .[226] Dabei bezeichnen die Bernoulli-Polynome. Die Aussage lässt sich sogar auf den Fall verallgemeinern, dass einen einfachen Pol im Ursprung mit Residuum hat. Gelten sonst alle Voraussetzungen wie oben, so gilt in dieser Situation für
gleichmäßig, sofern in .[227] Es bezeichnet das Landau-Symbol.
Holomorphie als Bedingung in Taubersätzen[Bearbeiten | Quelltext bearbeiten]
Taubersätze nutzen Eigenschaften von Potenz- oder Dirichlet-Reihen, um Aussagen über das Verhalten bestimmter Summen zu erhalten. Jedoch gelten diese oft nur unter technischen Bedingungen an die Funktion, die mit der zu untersuchenden Summe zusammenhängt. Holomorphie kann dabei helfen, die Bedingungen eines Taubersatzes zu erfüllen. Dies betrifft etwa einen Taubersatz von Donald Newman, der sich auf Dirichlet-Reihen bezieht: Ist
- wobei ,
mit für alle , und lässt sich holomorph auf die Gerade fortsetzen, so gilt bereits
Dieser Satz kann dazu verwendet werden, den Primzahlsatz mit einfachen funktionentheoretischen Methoden zu beweisen.[228] Ähnliche Aussagen gelten unter abgeschwächten Bedingungen, also ohne Holomorphie auf dem Rand, wie beim Satz von Wiener-Ikehara, doch dieser ist aus analytischer Sicht schwerer zu beweisen.[229]
Zu beachten ist, dass die analoge Aussage für Potenzreihen trivialerweise gilt. Ist also konvergent für und besitzt eine holomorphe Fortsetzung auf den Rand , so ist sogar absolut konvergent.
Integraltransformationen[Bearbeiten | Quelltext bearbeiten]
In einigen Anwendungen zu holomorphen Funktionen tauchen Integraltransformationen auf. Diese sind von der Form
wobei ein bestimmter Weg in der komplexen Ebene und eine geeignete, zu transformierende Funktion ist. Es ist der für die Art der Transformation eigentümliche Integralkern.
Allgemeine Holomorphieaussagen[Bearbeiten | Quelltext bearbeiten]
In vielen Fällen ist der Integrationsweg in einer Integraltransformation unendlich lang, weshalb neben der Leibnizschen Regel auch hier Kriterien geschaffen werden müssen, dass die Transformierte eine holomorphe Funktion ist. Dabei hilft: Es sei , eine offene Menge und eine stetige Funktion. Man bezeichnet das Integral
als gleichmäßig konvergent auf Kompakta in , falls existiert und gleichmäßig auf Kompakta in konvergiert. Trifft dies nun zu, und ist zudem für jedes holomorph, so ist holomorph auf , und es gilt
für alle .[230]
Holomorphie im Kontext bedeutender Integraltransformationen[Bearbeiten | Quelltext bearbeiten]
Fourier-Transformation[Bearbeiten | Quelltext bearbeiten]

Für den Fall, dass eine Funktion passende Bedingungen hinsichtlich Stetigkeit und Wachstum für erfüllt, kann ihre Fourier-Transformierte durch
definiert werden. Es gilt dann die Rücktransformation
Erfüllt die Wachstumsbedingung für Konstanten , so ist die Einschränkung auf einer auf dem Streifen holomorphen Funktion.[231] Der Satz von Paley-Wiener besagt ferner, dass wenn stetig ist und für für alle (d. h. moderat abklingt), sich zu einer ganzen Funktion fortsetzt mit für und alle , genau dann wenn der Träger von im Intervall liegt.[232] Klingen und beide moderat ab, so gilt für alle genau dann, wenn sich stetig auf die abgeschlossene obere Halbebene fortsetzt, dort beschränkt und in deren Innern zudem holomorph ist.[233]
Unter Ausnutzung, dass ihre eigene Fourier-Transformierte ist, kann zudem Folgendes gezeigt werden: Ist eine ganze Funktion mit mit , so lässt sich auch zu einer ganzen Funktion fortsetzen, und es gilt für irgendwelche .[234]
Mellin-Transformation[Bearbeiten | Quelltext bearbeiten]

Eng verwandt zur Fourier-Transformation ist die Mellin-Transformation, die definiert ist durch
Ist stückweise stetig[235] auf , erfüllt für und für , so ist eine im Streifen holomorphe Funktion.[236] Für den Fall, dass für schnell abklingt (etwa exponentiell), und zudem eine asymptotische Entwicklung der Form
für besitzt, lässt sich holomorph nach ganz fortsetzen mit Polen -ter Ordnung in und Hauptterm[237]
Besonders diese Eigenschaft macht die Mellin-Transformation bei der analytischen Fortsetzung von (verallgemeinerten) Dirichlet-Reihen zu einem nützlichen Werkzeug.[238]
Für eine im Streifen holomorphe Mellin-Transformierte gilt für alle die Umkehrformel
wobei nach Belieben gewählt werden darf.[239]
Laplace-Transformation[Bearbeiten | Quelltext bearbeiten]

Ist eine stückweise stetige Funktion, so ist ihre Laplace-Transformierte definiert durch
Ist für alle die Abschätzung für ein und ein , so ist eine auf der Halbebene holomorphe Funktion.[240] Gilt zusätzlich die Entwicklung
für , so folgt bereits
für .[241] Dieses Prinzip erweist sich zum Beispiel für den Beweis der Stirling-Formel, einer Approximation der natürlichen holomorphen Fortsetzung der Fakultätsfunktion durch einen geschlossenen Funktionsterm, als nützlich.[242]
Ist stückweise stetig und außerdem beschränkt, so folgt aus der holomorphen Fortsetzbarkeit von auf bereits, dass[243]
Ist nichtnegativ und nichtfallend, und ist holomorph auf , und gibt es eine Konstante , so dass
auf holomorph fortgesetzt werden kann, folgt[244]
Dies ist eine „holomorphe Variante“ des Satzes von Wiener-Ikehara, der auch für stetige Fortsetzungen funktioniert, jedoch unter diesen Umständen weitaus schwerer zu beweisen ist, wobei abkürzende Beweise im holomorphen Fall von Donald Newman und Jacob Korevaar gegeben wurden, die die durch die holomorphe Struktur verfügbare Cauchysche Integralformel benutzen.[245] Die holomorphe Variante reicht in vielen Fällen bereits aus. Es kann mit ihrer Hilfe schon der Primzahlsatz gezeigt werden.[246]
Algebraische Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Der Ring O(D) mit Gebiet D[Bearbeiten | Quelltext bearbeiten]
Durch komponentenweise Addition und Multiplikation wird die Menge zu einem kommutativen Ring mit 1 (nach Zulassen einer skalaren Multiplikation sogar zu einer -Algebra). Über den Identitätssatz für holomorphe Funktionen lässt sich zeigen, dass nullteilerfrei ist.[247] Es ist der Körper der meromorphen Funktionen gerade der Quotientenkörper von .[248]
Aus idealtheoretischer Sicht sind die Ringe schwieriger zu behandeln als zum Beispiel oder . Definiert man zu einer unendlich mächtigen, aber lokal endlichen Menge zum Beispiel das Ideal
so kann man folgern, dass nicht noethersch ist, also insbesondere niemals ein Hauptidealring.[249] Aus dem Produktsatz für allgemeine Gebiete lässt sich sogar folgern, dass nicht faktoriell ist.[250] Nichtsdestotrotz existieren gewisse Strukturen, so kann etwa nach dem Lemma von Wedderburn die 1 erzeugt werden:[251] Sind zwei zueinander teilerfremde holomorphe Funktionen (d. h., es gibt keine Nicht-Einheit , sodass ), so gibt es mit
Daraus kann gefolgert werden, dass zumindest jedes endlich erzeugte Ideal bereits ein Hauptideal ist.[252] Nach dem Hauptsatz der Idealtheorie in sind für ein Ideal sogar folgende Aussagen äquivalent:[253]
- ist endlich erzeugt.
- ist ein Hauptideal.
- ist abgeschlossen.
Dabei bedeutet Abgeschlossenheit, dass die Grenzfunktion jeder kompakt konvergenten Folge wieder in liegt.[254]
Die Sätze von Bers und Iss’sa[Bearbeiten | Quelltext bearbeiten]
Der Satz von Bers charakterisiert alle -Algebren-Homomorphismen zwischen -Algebren auf Gebieten holomorpher Funktionen.
Es seien Gebiete. Dann besagt der Satz von Bers: Zu jedem -Algebra-Homomorphismus gibt es genau eine Abbildung , sodass für alle . Es gilt und es ist genau dann bijektiv, wenn biholomorph ist.[255]
Es ist demnach biholomorph äquivalent zu genau dann, wenn (als -Algebren). Zudem ist jeder -Algebra-Homomorphismus von selbst stetig in dem Sinne, dass wenn kompakt konvergiert, bereits kompakt konvergiert.[255]
Ausgeweitet wird dieses Resultat durch den Satz von Iss’sa, da hier sogar der Körper der in bzw. meromorphen Funktionen betrachtet wird. Ist also ein Homomorphismus von -Algebren, so gibt es ein , sodass stets .[255]
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Holomorphe Funktionen werden systematisch im Rahmen der mathematischen Disziplin Funktionentheorie untersucht. Sie kommen zudem im Umfeld der reellen Analysis, theoretischen Physik, algebraischen Geometrie, Darstellungstheorie (im Kontext zu Modulformen), Kombinatorik, transzendenten Zahlen und analytischen Zahlentheorie zum Einsatz.
Bedeutung für die Physik[Bearbeiten | Quelltext bearbeiten]
In der theoretischen Physik treten holomorphe Funktionen unter anderem im Kontext zu Riemannschen Flächen auf. So spielt etwa der Raum aller holomorphen Funktionen von einer Riemannschen Fläche in eine -dimensionale Calabi-Yau-Mannigfaltigkeit eine wichtige Rolle in Mirror Symmetry, die in der Stringtheorie Anwendung findet.[256]
Anwendung in der Zahlentheorie[Bearbeiten | Quelltext bearbeiten]
Dirichlet-Reihen[Bearbeiten | Quelltext bearbeiten]
Wächst eine zahlentheoretische Funktion nicht zu schnell, also für eine reelle Konstante , so wird für alle komplexen Werte mit die Reihe
absolut konvergieren. Man bezeichnet diesen Typ Reihe auch als Dirichlet-Reihe. Es gibt dann eine Konstante , die Konvergenzabszisse, sodass die Reihe für alle Werte bedingt konvergiert und für divergiert. Es kann gezeigt werden, dass die Reihe auf kompakten Teilmengen gleichmäßig konvergiert, womit sie eine auf der Halbebene holomorphe Funktion ist.
Ähnlich wie Potenzreihen dienen Dirichlet-Reihen dazu, zahlentheoretische Funktionen zu untersuchen. Etwa kann die Holomorphie von Dirichlet-Reihen dazu verwendet werden, die Perronschen Formeln zu zeigen, um summatorische Funktionen zu studieren. Während Potenzreihen besonders in der additiven Zahlentheorie Anwendung finden, treten Dirichlet-Reihen vor allem in der multiplikativen Zahlentheorie auf. Ein wichtiges Beispiel ist die Riemannsche Zeta-Funktion
die sogar auf ganz holomorph fortgesetzt werden kann. Durch ihre Verbindung zu den Primzahlen (siehe Euler-Produkt) spielt sie eine Schlüsselrolle in der analytischen Zahlentheorie. Aufgrund ihrer Holomorphie ist es möglich, exakte Informationen über Primzahlen aus ihrem Verhalten als Funktion, wie zum Beispiel der Verteilung ihrer Nullstellen, abzuleiten. Dies betrifft zum Beispiel den Primzahlsatz, der jedoch unter Annahme der Riemannschen Vermutung deutlich verbessert werden kann.[257] Die weitaus allgemeineren L-Funktionen sind ebenso von großer Wichtigkeit in der Zahlentheorie. Dies betrifft etwa den Modularitätssatz, aber auch die Vermutung von Birch und Swinnerton-Dyer.[258]
Modulformen und q-Reihen[Bearbeiten | Quelltext bearbeiten]
Klassische Modulformen sind auf der oberen Halbebene holomorphe Funktionen , die bestimmte Transformationsgestze bezüglich Untergruppen endlichen Indexes erfüllen und ein „holomorphes Verhalten“ in den Randpunkten aufweisen, zum Beispiel durch Besitz eine Fourier-Entwicklung der Form
- mit einer natürlichen Zahl .
Die Bedingung der Holomorphie liefert dabei eine entscheidende Zutat für die Seltenheit von Modulformen, da sie im Beweis der Valenzformel (in Form des Null- und Polstellen zählenden Integrals) eingeht. Aus dieser kann gefolgert werden, dass der Raum aller Modulformen eines festen Gewichts bezüglich einer Kongruenzuntergruppe stets endlichdimensional ist, was weitreichende Konsequenzen nach sich zieht.[259]
Kreismethode[Bearbeiten | Quelltext bearbeiten]
Die Kreismethode gehört zu den wichtigsten Anwendungen holomorpher Funktionen in der Zahlentheorie. Ausgangspunkt ist eine Folge ganzer Zahlen , die nicht zu schnell anwachsen, und deren Wachstumsverhalten man verstehen möchte. Betrachtet wird dann die Funktion
wobei die Reihe für konvergieren, und für divergieren soll. Dies ist zum Beispiel dann der Fall, wenn die mit polynomieller Geschwindigkeit wachsen oder bis auf eine Konstante kleiner als für ein sind. Über die Cauchysche Integralformel erhält man
wenn der geschlossene Weg, etwa ein Kreis mit Radius , die 0 einfach in mathematisch positiver Richtung umschließt. Dabei ist es üblich, den Radius der Integrationskurve in Abhängigkeit von zu wählen, also , und für mit richtiger Konvergenzgeschwindigkeit zu fordern. Ist die Folge positiv und monoton steigend, ist davon auszugehen, dass in der Nähe von unendlich groß wird und dieses Wachstum das Verhalten an allen anderen Randpunkten dominiert. Daher sollte der Integrationsabschnitt in der Nähe von auch den ausschlaggebenden Beitrag für den Wert der liefern. Ein detailliertes Studium der Funktion in der Nähe von , aber auch ggf. anderer Randwerte, kann also zu einem Verständnis der führen.

Erstmals wurde die Kreismethode von Godfrey Harold Hardy und Srinivasa Ramanujan angewandt, um die Partitionsfunktion zu untersuchen.[260] Ihnen gelang mit ihrer Hilfe die asymptotische Schätzung[261]
Als Ausgangspunkt diente die für alle gültige, von Leonhard Euler gefundene,[262] Identität
Hans Rademacher konnte mit ähnlichen Methoden sogar eine exakte Formel für ableiten.[263] Seine Methode nutzt die Modularität der Dedekindschen Etafunktion.[264] Weitere Anwendungen liegen im Umfeld des Waringschen Problems[265] und allgemein Lösungsanzahlen diophantischer Gleichungen.[266]
Komplexe Geometrie[Bearbeiten | Quelltext bearbeiten]
Auch in der komplexen Geometrie werden holomorphe Abbildungen betrachtet. So kann man holomorphe Abbildungen zwischen Riemannschen Flächen oder zwischen komplexen Mannigfaltigkeiten analog zu differenzierbaren Funktionen zwischen glatten Mannigfaltigkeiten definieren.[267] Außerdem gibt es ein für die Integrationstheorie wichtiges Pendant zu den glatten Differentialformen, das holomorphe Differentialform heißt.[268]
Holomorphe Funktionen mehrerer Veränderlicher[Bearbeiten | Quelltext bearbeiten]
Sei eine offene Teilmenge. Eine Abbildung heißt holomorph, falls sie sich um jeden Punkt des Definitionsbereichs in eine Potenzreihe entwickeln lässt, das heißt, zu jedem gibt es einen Polykreis , sodass
für alle mit von unabhängigen Koeffizienten gilt.[269] Eine Funktion heißt holomorph in der -ten Variablen, wenn sie als Funktion von bei festgehaltenen übrigen Variablen holomorph ist. Holomorphe Funktionen sind natürlich in jeder Variablen holomorph. Für die Umkehrung siehe die untenstehenden äquivalenten Charakterisierungen.
Mit dem Wirtinger-Kalkül und steht ein Kalkül zur Verfügung, mit dem man die partiellen Ableitungen einer komplexen Funktion wie bei Funktionen einer Veränderlichen behandeln kann.
Für eine Funktion , offen, sind folgende Aussagen äquivalent:[270]
- ist holomorph.
- ist stetig und holomorph in jeder Variablen (Lemma von Osgood)
- ist holomorph in jeder Variablen (Satz von Hartogs)
- ist stetig differenzierbar und genügt den Cauchy-Riemannschen Differentialgleichungen für .
Für mehrere Dimensionen im Bildbereich definiert man Holomorphie wie folgt: Eine Abbildung , offen, heißt holomorph, wenn jede der Teilfunktionen holomorph ist.[271]
Viele Eigenschaften holomorpher Funktionen einer Veränderlichen lassen sich, teils in abgeschwächter Form, auf den Fall mehrerer Veränderlicher übertragen. So gilt für Funktionen der Cauchysche Integralsatz nicht und der Identitätssatz ist nur noch in einer abgeschwächten Version gültig.[272] Für holomorphe Funktionen kann allerdings die Integralformel von Cauchy durch Induktion auf Dimensionen verallgemeinert werden.[273] Salomon Bochner konnte 1944 sogar noch eine Verallgemeinerung der -dimensionalen Cauchyschen Integralformel beweisen. Diese trägt den Namen Bochner-Martinelli-Formel.
Literatur[Bearbeiten | Quelltext bearbeiten]
- John B. Conway: Functions of One Complex Variable I. 2. Auflage. Springer, 1978, ISBN 0-387-90328-3.
- John B. Conway: Functions of One Complex Variable II. Springer, 1995, ISBN 0-387-94460-5.
- Wolfgang Fischer, Ingo Lieb: Funktionentheorie – Komplexe Analysis in einer Veränderlichen. 8. Auflage. Vieweg, Braunschweig/Wiesbaden 2003, ISBN 3-528-77247-6.
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3. Auflage. Springer, 2000, ISBN 3-540-67641-4.
- Eberhard Freitag: Funktionentheorie 2. Riemann’sche Flächen; Mehrere komplexe Variable; Abel’sche Funktionen; Höhere Modulformen. Springer, 2009, ISBN 978-3-540-87899-5.
- Klaus Jänich: (Die ersten beiden Auflagen unterscheiden sich deutlich von den folgenden. Unter anderem fehlen ab der dritten Auflage die vier „Stern“-Kapitel zu Wirtinger-Kalkül, riemannschen Flächen, riemannschen Flächen eines holomorphen Keimes und algebraischen Funktionen.)
- Einführung in die Funktionentheorie. 2. Auflage. Springer-Verlag, Berlin/Heidelberg 1980, ISBN 3-540-10032-6.
- Funktionentheorie – Eine Einführung. 6. Auflage. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-20392-3.
- Serge Lang: Complex Analysis. 4. Auflage. Springer, 1999, ISBN 0-387-98592-1.
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, ISBN 3-540-41855-5.
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 2. 3. Auflage. Springer, Heidelberg 2007, ISBN 978-3-540-40432-3.
- Elias Stein, Rami Shakarchi: Complex Analysis. Princeton University Press, Princeton 2003, ISBN 0-691-11385-8.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Elias Wegert: Visualization of Complex Functions – Plea for the Phase Plot –, Technical University Freiberg, 2009, S. 1.
- ↑ Elias Wegert: Visualization of Complex Functions – Plea for the Phase Plot –, Technical University Freiberg, 2009, S. 3–4.
- ↑ Wolfram Language. 2019. ComplexPlot. Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020, abgerufen am 12. September 2021.
- ↑ Frank A. Farris, Visualizing complex-valued functions in the plane, abgerufen am 12. September 2021.
- ↑ David A. Rabenhorst: A Color Gallery of Complex Functions. In: Pixel: The Magazine of Scientific Visualization. 1. Jahrgang, Nr. 4. Pixel Communications, 1990, S. 42 ff. (google.com).
- ↑ Elias Wegert: Visual Complex Functions: An Introduction with Phase Portraits. Springer Basel, 2012, ISBN 978-3-0348-0179-9, S. 29 (springer.com [abgerufen am 12. September 2021]).
- ↑ Douglas N. Arnold: Graphics for complex analysis. 2008, abgerufen am 12. September 2021.
- ↑ Frank A. Farris: Creating Symmetry: The Artful Mathematics of Wallpaper Patterns. Princeton University Press, 2015, ISBN 978-0-691-16173-0, S. 36–37 (google.com).
- ↑ Peter Kovesi: Colour Maps for the Colour Blind, presented at IAMG 2017. 2017.
- ↑ Henri Cohen, Fredrik Strömberg: Modular Forms, American Mathematical Society, Volume 179, S. 404.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 120.
- ↑ J. H. Brunier, G. van der Geer, G. Harder, D. Zagier: The 1-2-3 of Modular Forms, Lectures at a Summer School in Nordfjordeid, Norway, Springer-Verlag Berlin Heidelberg, S. 27.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 92.
- ↑ David Wakeman: String perturbation theory and Riemann surfaces, 2018, S. 1.
- ↑ Barton Zwiebach: A First Course in String Theory, Second Edition, Cambridge University Press, S. 591.
- ↑ a b c Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 56.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 386.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 35.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 9.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 10.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 45.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 91.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 108.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 52–53.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 69.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 68.
- ↑ Klaus Gürlebeck, Klaus Habetha und Wolfgang Sprößig: Funktionentheorie in der Ebene und im Raum, Birkhäuser, S. 10–11.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 42.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 52.
- ↑ a b Devrim Cakmak, Aydin Tiryaki: Meam value theorem for holomorphic functions, Electronic Journal of Differential Equations, Vol. 2012, 2012, No. 34, S. 5.
- ↑ Bruce P. Palka: An Introduction to Complex Function Theory, Undergraduate Texts in Mathematics, Springer, S. 304.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 64.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 66.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 67.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 63.
- ↑ Bruce P. Palka: An Introduction to Complex Function Theory, Undergraduate Texts in Mathematics, Springer, S. 188.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 212.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 91.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 79.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 79–80.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 184.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 182.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 90.
- ↑ a b c Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 189.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 187.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 183.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 185.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 186.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 118.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 190.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 3.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 193.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 99.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 100.
- ↑ a b Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation, The Ramanujan Journal, doi:10.1007/s11139-020-00377-5, 2021, S. 18.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 195.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 114.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 135.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 209.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 137.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 136.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 142.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 140.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 144.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 149.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 148.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 335.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 156.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 19.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 38.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 47.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 22.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 48.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 38.
- ↑ Klaus Gürlebeck, Klaus Habetha und Wolfgang Sprößig: Funktionentheorie in der Ebene und im Raum, Birkhäuser, S. 228.
- ↑ Klaus Gürlebeck, Klaus Habetha und Wolfgang Sprößig: Funktionentheorie in der Ebene und im Raum, Birkhäuser, S. 230.
- ↑ W. F. Osgood: Lehrbuch der Funktionentheorie. Erster Band., Fünfte Auflage, Chelsea Publishing Company Bronx, N. Y., S. 357.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 108.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 242.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 207.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 173.
- ↑ a b John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 281.
- ↑ a b c Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 130.
- ↑ a b c Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 145.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 131.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 132.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 134.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 135.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 153.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 17.
- ↑ W. F. Osgood: Lehrbuch der Funktionentheorie. Erster Band., Fünfte Auflage, Chelsea Publishing Company Bronx, N. Y., S. 340.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 258.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 269.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 164.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 171.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 180.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 184.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 187.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 190.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 178–179.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 120.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 121.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 123.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 124.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 229.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 124–125.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 125.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 138.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 138–139.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 366.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 124.
- ↑ Toshitsune Miyake: Modular Forms, Springer, S. 118.
- ↑ a b Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 369.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 368.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 370.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 91.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 91–92.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 157.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 138.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 444.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 96.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 297.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 129.
- ↑ S. Ruscheweyh, T. Sheil-Small: Hadamard products of schlicht functions and the Polya-Schoenberg conjecture, Comment. Math. Helv., 48, 1973, 119–135.
- ↑ John L. Lewis: Convexity of a certain series, J. London Math. Soc. (2), 27, 1983, 435–446, S. 435.
- ↑ A. W. Goodman: On Uniformly Starlike Functions, Journal of Mathematical Analysis and Applications, 155, S. 364–370.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, S. 243.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 448.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 293.
- ↑ Lars V. Ahlfors, Helmut Grunsky: Über die Blochsche Konstante, 9. Dezember 1936, Mathematische Zeitschrift 42, Dezember 1937, S. 671–673.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 295.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 298.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 299.
- ↑ Peter L. Duren: Univalent Functions, Springer, S. 31.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 109.
- ↑ Alan Gluchoff und Frederick Hartmann: Univalent polynomials and non-negative trigonometric sums. Amer. Math. Monthly, 1998, 105(6):508– 522, S. 513.
- ↑ Harald Bohr: A theorem concerning power series. Proc. Lond. Math. Soc., 13 (2), 1914, S. 1–5
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 136.
- ↑ a b c Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 100.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, S. 232.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 101.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 55–56.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 195–196.
- ↑ a b Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 162.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 163.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 472.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 464.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 234–235.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 233.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 157.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 463.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 274–275.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 151.
- ↑ Alan Beardon, David Minda: On the pointwise Limit of Complex Analytic Functions, The American Mathematical Monthly, Vol. 110, No. 4, S. 292.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 460.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 238.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 50.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 50.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 49.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 214.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 12.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 170.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 173.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 222.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 342.
- ↑ Maurice Heins: Complex Function Theory, Academic Press, 1968, S. 317.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 116–117.
- ↑ Gérald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, American Mathematical Society, Volume 163, S. 242.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 116.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 216.
- ↑ Bruce P. Palka: An Introduction to Complex Function Theory, Undergraduate Texts in Mathematics, Springer, S. 167.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 197.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 118.
- ↑ W. Bridges, J. Franke, und T. Garnowski: Asymptotics for the twisted eta-product and applications to sign changes in partitions. Res Math Sci 9, 61, 2022, S. 7.
- ↑ Terry Sheil-Small: Complex Polynomials, Cambridge Studies in advanced mathematics, 75, Cambridge University Press, S. 129–130.
- ↑ Peter L. Duren: Univalent Functions, Springer, S. 122.
- ↑ Peter L. Duren: Univalent Functions, Springer, S. 143.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 149.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 148.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 136.
- ↑ G. Polya und G. Szego: Aufgaben und Lehrsätze aus der Analysis. Erster Band., Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Band 19, Dritte Auflage, Springer, S. 137.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 301.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 301–309.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 315.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie, Springer, 1995, S. 76.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie, Springer, 1995, S. 77.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 151–152.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 386.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 219.
- ↑ a b Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 360.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 360–361.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 194.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 122.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 161.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 95–96.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 114–115.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 115.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 227.
- ↑ Klas Diederich, Reinhold Remmert: Funktionentheorie I, Springer, S. 147.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 22.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane, Birkhäuser, S. 483.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 188.
- ↑ Philip Morse, Herman Feshbach: Methods of Theoretical Physics, Part I. New York: McGraw-Hill, 1953, S. 412.
- ↑ Eric W. Weisstein: Series Reversion. In: MathWorld (englisch). Abgerufen am 11. Mai 2021.
- ↑ a b Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 228.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 239.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 186.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 228.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 187.
- ↑ a b Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 188.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 279.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 127.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 126.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 280.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 215.
- ↑ Serge Lang: Complex Analysis, Fourth Edition, Springer, S. 216.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 155.
- ↑ Alexander Isaev: Twenty-One Lectures on Complex Analysis, Springer, S. 33–38.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 281.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 262.
- ↑ Nico Temme: Asymptotic Methods for Integrals, Series in Analysis Vol. 6, World Scientific, S. 10.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 263.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 264.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 265.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, S. 266.
- ↑ Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation, The Ramanujan Journal, doi:10.1007/s11139-020-00377-5, 2021, S. 4–5.
- ↑ Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation, The Ramanujan Journal, doi:10.1007/s11139-020-00377-5, 2021, S. 5.
- ↑ D. Zagier: Newman’s short proof of the prime number theorem. In: The American Mathematical Monthly, Bd. 104, Nr. 8 (Oktober 1997), S. 705–708 (PDF).
- ↑ Donald J. Newman: Analytic Number Theory, Springer, S. 67.
- ↑ John B. Conway: Functions of One Complex Variable I, Second Edition, Springer, S. 154.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 121.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 122.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 126.
- ↑ Elias Stein, Rami Shakarchi: Complex Analysis, Princeton University Press, S. 130.
- ↑ Eberhard Zeidler: Quantum Field Theory I. Basics in Mathematics and Physics., Springer, Appendix zur Mellin-Transformation und anderer nützlicher analytischer Techniken von Don Zagier, S. 305.
- ↑ Eberhard Zeidler: Quantum Field Theory I. Basics in Mathematics and Physics., Springer, Appendix zur Mellin-Transformation und anderer nützlicher analytischer Techniken von Don Zagier, S. 306.
- ↑ Eberhard Zeidler: Quantum Field Theory I. Basics in Mathematics and Physics., Springer, Appendix zur Mellin-Transformation und anderer nützlicher analytischer Techniken von Don Zagier, S. 307.
- ↑ Eberhard Zeidler: Quantum Field Theory I. Basics in Mathematics and Physics., Springer, Appendix zur Mellin-Transformation und anderer nützlicher analytischer Techniken von Don Zagier, S. 311.
- ↑ Lokenath Debnath, Dambaru Bhatta: Integral Transforms and Their Applications, Second Edition, Chapman & Hall, S. 340.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 365.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 366.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 368.
- ↑ Theodore Gamelin: Complex Analysis, Springer, S. 385.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 281.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 287.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 281–287.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 123.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, S. 285.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 138.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 96.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 139.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 140.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 142.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 141.
- ↑ a b c Reinhold Remmert, Georg Schumacher: Funktionentheorie 2, 3. Auflage, Springer, S. 110.
- ↑ Kentaro Hori et al.: Mirror Symmetry, Clay Mathematics Monographs, Vol. 1, S. 55.
- ↑ Gérald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, American Mathematical Society, Volume 163, S. 271.
- ↑ John Coats: The Conjecture of Birch and Swinnerton-Dyer. In: Open Problems in Mathematics. Hrsg.: John Forbes Nash u. Michael Th. Rassias, Springer, S. 209.
- ↑ J. H. Brunier, G. van der Geer, G. Harder, D. Zagier: The 1-2-3 of Modular Forms, Lectures at a Summer School in Nordfjordeid, Norway, Springer-Verlag, Berlin/Heidelberg, S. 12.
- ↑ G. Hardy, S. Ramanujan: Asymptotic Formulæ in Combinatory Analysis, Proceedings of the London Mathematical Society (2), Vol. 17, (1918), S. 75–115.
- ↑ George Andrews: The Theory of Partitions, Cambridge Mathematical Library, S. 70.
- ↑ Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory, Second Edition, Springer, S. 94.
- ↑ Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory, Second Edition, Springer, S. 94–95.
- ↑ Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory, Second Edition, Springer, S. 96.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 112–113.
- ↑ Marius Overholt: A Course in Analytic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Vol. 160, S. 111 ff.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 13 ff.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 187.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 314–315.
- ↑ Gunning-Rossi: Analytic functions of several complex variables. Prentice-Hall 1965, Kap. I.A: The Elementary Properties of Holomorphic Functions.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 319.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 322–323.
- ↑ Eberhard Freitag: Funktionentheorie 2, Springer, S. 315.































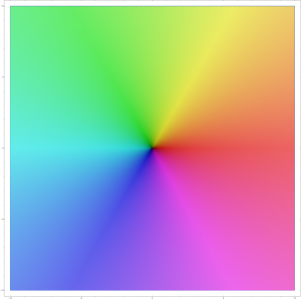

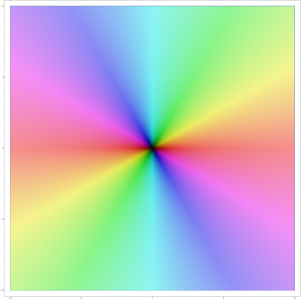
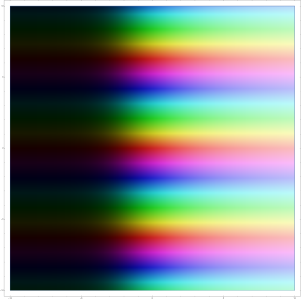
































































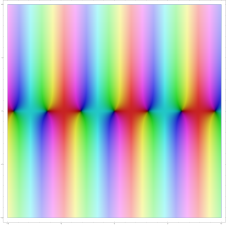
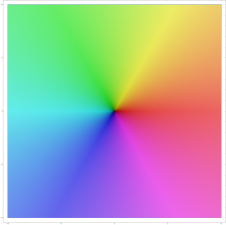



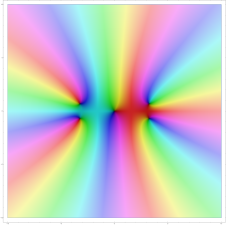

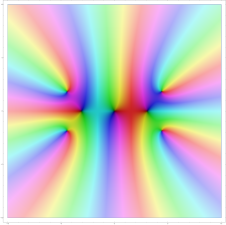





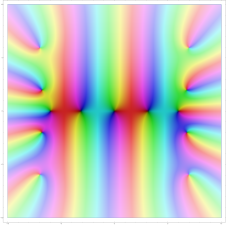






































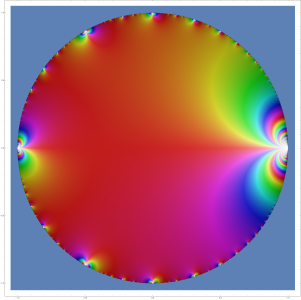





















































































































![{\displaystyle \gamma \colon [0,1]\to D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e472a1bd16d5c728ffc1aa8727e1585c9695548b)
























































![{\displaystyle R={\frac {1}{\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55eb6ac596939b67ff78b5333791282696869b43)















































































































![{\displaystyle z\in \gamma ([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cff517f0167179cda5f6c1773335081c1505b88)
![{\displaystyle \gamma ([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8899198b84485947179f1d5095f747700b0e8947)















































![{\displaystyle \gamma \colon [0,1]\to D\setminus \{a_{1},\dots ,a_{n}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f88665ca4b975052d536c55e5886fe84f843cb)























![{\displaystyle \sin(\mathbb {R} )=[-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4fb5152a67f71675a6c90a2f7840c19c3a307a0)






















































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





















































































![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
















![{\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccf6eb823414cc4f75e408522881f3423c52534d)






![{\displaystyle U\times [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e232769cc6acd51e363a7a8c3c02edd10669a28b)















































































































![{\displaystyle |f(z_{1})-f(z_{2})|=\left|\int _{z_{2}}^{z_{1}}f'(z)\mathrm {d} z\right|\leq |z_{1}-z_{2}|\max _{z\in [z_{1},z_{2}]}|f'(z)|\leq |z_{1}-z_{2}|\max _{|z-c|=r}|f'(z)|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77b2baf26bf22d0f4b277a235baa7e84bb79da46)


![{\displaystyle [z_{1},z_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba07875e5770e72f22fe18b97ae96a10f343252)
![{\displaystyle \left|{\frac {f(z_{1})-f(z_{2})}{z_{1}-z_{2}}}\right|\leq \max _{z\in [z_{1},z_{2}]}|f'(z)|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eebf9218eb656b55f87632871c018a16b28baef0)





































































![{\displaystyle \mathbb {C} [z]\subset {\mathcal {O}}({\mathcal {\mathbb {C} }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ebb7ef3bdf42818ec8d2d10793edc2853d4190)








![{\displaystyle \mathbb {Q} [f_{1},\dots ,f_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0f05de9dd829637c8fde98815c0ed07a02bc51)








![{\displaystyle \mathbb {Q} [z,e^{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f014d936bb8379b11c0750e72b85939d76852cc7)

































































































![{\displaystyle f\mapsto [M_{f}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3214a5d555f6b1409d38a2d95a5c50b2fd81755)























![{\displaystyle [c_{\nu },z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea94fea573d1d659afc1dff34924740c9e9e7ffd)
















































![{\displaystyle [-M,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/476bee11bf7b2b0731edbbc3c28227deb0f460b6)












































![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)






























































