Loxodrome

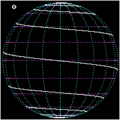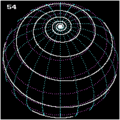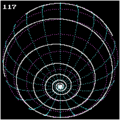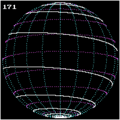
Eine Loxodrome (gr. loxos „schief“, dromos „Lauf“) ist eine Kurve auf einer Kugeloberfläche – z. B. der Erdoberfläche –, die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird.
Allgemeiner gibt es zu jedem Rotationskörper Loxodromen als Kurven konstanten Kurses. Die Loxodromen der Kugel heißen speziell Kugelloxodromen, Loxodromen eines Zylinders sind Schraubenlinien, die des Kegels sind konische Spiralen (konische Helizes).
Loxodromen wurden um 1550 von Pedro Nunes entdeckt, der Name stammt von Willebrord Snell (1624).
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
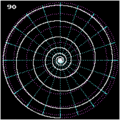
Außer in Spezialfällen, Schnittwinkel 0° und 90° mit den Meridianen, sind Loxodromen nicht geschlossen. Sie winden sich spiralförmig um die Erde herum und nähern sich dabei den Polen an. Im strengen Sinn erreicht eine Loxodrome zwar nach einer endlichen Strecke nie den Pol, nähert sich ihm jedoch asymptotisch an, indem sie sich unendlich oft um ihn windet. In Polnähe hat eine Loxodrome also lokal die Eigenschaften einer (ebenen) Spirale, in Äquatornähe dagegen Eigenschaften einer Helix (räumliche Wendel).
Beim Spezialfall eines Schnittwinkels mit einem Meridian von 0° ist die Loxodrome selbst ein Meridian und somit ein Großkreis, der durch die Pole geht. Das ist der einzige Fall einer Loxodrome, die den Pol erreicht. Daraus ergibt sich im Umkehrschluss: Da einzig und allein die Loxodromen mit 0° den Nordpol erreichen, starten umgekehrt vom Nordpol auch nur Loxodromen mit 180°. Vom geographischen Nordpol aus kommt man also nur in Richtung 180° weg – allerdings ist die Kursangabe 180° am Nordpol nicht definiert: Man könnte sich mit diesem Kurs vom Nordpol aus auf jedem Meridian bewegen. Lediglich die Ankunft am Südpol wird damit garantiert. In der praktischen Navigation wird dieses Problem umgangen, indem in hohen Breitengraden nach der Gitternavigation (engl. grid navigation) mit polarstereographischen Karten gearbeitet wird.
Beim zweiten Spezialfall – Schnittwinkel 90° – ist die Loxodrome ebenfalls geschlossen, sie bildet einen Breitenkreis (Breitenparallel), ist also im Allgemeinen kein Großkreis. Der einzige Breitenkreis, der ein Großkreis ist, ist der Äquator, also diejenige Loxodrome, auf der die geographische Breite konstant 0° beträgt.
Projektionen:
- In der Kartografie werden auf Karten in der Mercator-Projektion die Loxodromen als gerade Linien abgebildet. Darauf beruht der Nutzen der Mercatorkarte für die praktische Navigation.
- In einer stereografischen Projektion wird die Kurve zu einer logarithmischen Spirale
- In einer orthografischen Azimutalprojektion (Parallelriss entlang der Erdachse) entsteht eine Poinsotsche Spirale
-
Animation einer Loxodrome
-
Loxodrome am Pol
-
Loxodrome am Äquator
Berechnung[Bearbeiten | Quelltext bearbeiten]
Die Formel der Loxodrome (der Steigungswinkel in der Projektion) leitet sich aus der erwähnten Eigenschaft der Mercatorprojektion her, Loxodromen als Geraden abzubilden.
In Richtung Westen ist negativ, Richtung Osten positiv; ist positiv für Breiten der Nordhemisphäre und negativ auf der Südhalbkugel. Beide Winkel werden hier mathematisch im Bogenmaß verwendet, nicht in Grad
- der Richtungswinkel ist eine konstante Peilung in Richtung wahrer Norden, der Steigungswinkel in der Mercatorprojektion, mit der Steigung
In Raumkoordinaten[Bearbeiten | Quelltext bearbeiten]
Sei die Längenkoordinate eines beliebigen Punktes der Loxodrome (wobei nicht auf beschränkt ist).
In der Mercatorprojektion ist die Kurve eine Gerade:
Für einen Punkt der Breite und Länge gilt aufgrund der Abbildungvorschrift der Mercatorprojektion
Für die Breite des Punkts ergibt sich also
oder, als Gudermannfunktion gd ausgedrückt,
In kartesischen Koordinaten, mit als Radius einer Kugel:
Diese Kurve geht bei geographischer Länge durch den Äquator, für beliebige Lagen des Äquatordurchgangs ist , und in den obigen Formeln ist der Ausdruck entsprechend zu ersetzen.
In der Mercatorprojektion[Bearbeiten | Quelltext bearbeiten]

| Weg | Lox. | Orth. | Diff. |
|---|---|---|---|
| NY-MO | 8359 km | 7511 km | 10,1 % |
| NY-DA | 6207 km | 6150 km | 0,9 % |
| DA-MO | 6596 km | 6509 km | 1,3 % |
In der Luft- und insbesondere der Seefahrt kann es günstig sein, entlang einer Loxodrome zu reisen, da man dann immer nur einer Peilung (Kompassrichtung) folgen muss. Zwar ist die Strecke der Loxodrome immer länger als die der Orthodrome (nur wenn die Loxodrome auf einem Großkreis liegt, können sie gleich lang sein) – dafür muss man aber nicht ständig einen neuen Kurswinkel berechnen. Auf kürzeren Strecken ist die Navigation auf der Loxodrome nur unwesentlich länger als die Navigation auf der Orthodrome. Im Flugverkehr hingegen werden Lamberts winkeltreue Kegelprojektionen verwendet.
Die Mercatorprojektion bildet einen Punkt mit den Koordinaten auf die ebenen Koordinaten ab, wobei:
- mit der inversen Gudermannfunktion.
Durch die Mercatorprojektion zweier Punkte und entsteht in der Projektionsebene ein rechtwinkliges Dreieck mit als Hypotenuse und dem rechten Winkel bei . Für den Winkel bei ergibt sich:
Unter Verwendung der zweistelligen Funktion die zu den kartesischen Koordinaten den Winkel der Polarkoordinatendarstellung liefert und als arctan2- oder atan2-Funktion in vielen Programmiersprachen zur Verfügung steht, erhält man:
Der Richtungswinkel der Loxodrome, der von Nord über Ost im Uhrzeigersinn berechnet wird, ist dann:
Die Strecke, die man – innerhalb der Mercatorkarte – zwischen Punkt A und B auf der Loxodrome zurücklegt, beträgt:
Zu beachten ist, dass dies nur die kürzeste Loxodrome ist, wenn gilt, sie also in Westrichtung weiter voneinander entfernt sind als in Ostrichtung, im anderen Falle ist das nur der zweitbeste Weg. Außerdem lässt sich zwischen zwei beliebigen Punkten (außer den Polen) immer eine beliebige Anzahl an Loxodromen finden, die dann einmal oder mehrmals die Kugel (Erde) umrunden. Für diese Fälle ist in der anfänglichen Gleichung für ein anderer Nebenwert des Tangens zu wählen. In der Mercatorprojektion wandert der Graph dabei über den rechten oder linken Rand hinaus und erscheint auf der anderen Seite wieder.