Pollard-Rho-Methode

Die Pollard-Rho-Methoden sind Algorithmen zur Bestimmung der Periodenlänge einer Zahlenfolge, die mit einer mathematischen Funktion berechnet wird. Verschiedene schwierige mathematische Probleme wie der diskrete Logarithmus und die Faktorisierung lassen sich mit diesen Methoden berechnen. Eine optimierte Variante der Pollard-Rho-Methode wurde von John M. Pollard im Jahre 1975 zur Primfaktorzerlegung entwickelt. Derartige Verfahren lassen sich auch zur Berechnung von Kollisionen in Hash-Funktionen anwenden.
Bei den Pollard-Rho-Methoden werden Folgen von Teilergebnissen berechnet. Ab einem bestimmten Punkt wiederholt sich ein Teil dieser Teilergebnisse nur noch. Man kann die Teilergebnisse grafisch so anordnen, dass sich die Gestalt des Buchstaben ρ (Rho) erkennen lässt. Daraus leitet sich die Bezeichnung der Methoden ab.
Funktionsweise[Bearbeiten | Quelltext bearbeiten]
Gesucht ist ein Primfaktor der Zahl . Im Allgemeinen muss dieser Teiler jedoch nicht zwingend eine Primzahl sein. Das Verfahren beruht auf der Erzeugung einer Folge von Pseudozufallszahlen. Zur Erstellung der Zufallsfolge kann eine relativ beliebige Funktion verwendet werden. Es ist lediglich erforderlich, dass aus auch folgt, und dies gilt beispielsweise bereits, wenn durch ein Polynom mit ganzzahligen Koeffizienten gegeben ist.
Die Folge startet mit einem weitgehend beliebig wählbaren Startwert . Die weiteren Werte werden iterativ berechnet gemäß
Die Funktionswerte modulo können maximal die verschiedenen Werte annehmen. Tritt einer dieser Werte erneut auf, so wiederholen sich anschließend diese Werte modulo . Dies geschieht spätestens nach Iterationen und im Mittel nach etwa Iterationen. Aus denselben Gründen kann man nach etwa Iterationen erwarten, dass sich die Werte modulo wiederholen. Wenn bereits bekannt ist, dass einen kleinen Primfaktor hat, ist erheblich kleiner als , so dass gehofft werden darf, dass die Wiederholung modulo erheblich früher als die Wiederholung modulo einsetzt.
Bei einer derart berechneten Zahlenfolge mit endlich vielen möglichen Funktionswerten werden zunächst in einer Vorperiode einige Werte
angenommen. Sobald ein Wert wiederholt auftritt, wiederholen sich die Werte anschließend zyklisch
Dieses Verhalten der Folge gab der Methode ihren Namen, da man sich die Periode wie einen Kreis vorstellen kann und die Folgenglieder am Anfang wie einen Stängel, der in den Kreis hineinführt. Graphisch sieht das aus wie der griechische Buchstabe ρ.
Haben zwei Werte und modulo aus der Folge den gleichen Wert, für die folglich gilt, so ergibt der größte gemeinsame Teiler ein Vielfaches von und oftmals einen echten Teiler von .
Es ist jedoch sehr aufwändig, alle Zahlenwerte auf diese Weise zu vergleichen. Eine optimierte Variante der Pollard-Rho-Methode berechnet daher zur Bestimmung der Periodenlänge zwei Folgen. Eine Folge
und die zweite Folge
Durch diesen Trick kann der Vergleich sehr vieler Funktionswerte vermieden werden. Es muss jetzt nicht für alle Paare der größte gemeinsame Teiler berechnet werden. Es genügt jeweils, bzw. zu berechnen.
Da , als ein gesuchter Teiler von , unbekannt ist, kann zunächst der Rest der Division durch nicht berechnet werden. Es wird daher nicht die Gleichheit zweier Werte und abgefragt, sondern der berechnet. Falls sich die Werte und nur um ein Vielfaches von unterscheiden, ist der Wert des ein Vielfaches des gesuchten Teilers von . Ganzzahlige Vielfache von sind zugleich ganzzahlige Vielfache von und brauchen deshalb bei der Berechnung nicht berücksichtigt werden. Infolgedessen genügt es die Funktionswerte modulo zu berechnen.
Zur Berechnung der Zahlenfolge kann eine Funktion der Form benutzt werden. Durch diese Wahl können nur ein Teil, etwa die Hälfte, der Werte bis bei der Restbildung auftreten, wodurch das frühzeitigere Auftreten der gesuchten Wiederholungen etwas begünstigt wird.
Formale Definition[Bearbeiten | Quelltext bearbeiten]
Sei die Zahl, von der ein Primfaktor berechnet werden soll. Bezeichne eine Folge von Pseudozufallszahlen wie zum Beispiel
Existiert ein echter Primfaktor , so gilt
- Es gibt einen Index , so dass und mit .
Algorithmus[Bearbeiten | Quelltext bearbeiten]
Eingabe: ist die zu faktorisierende Zahl und sei die Pseudo-Zufallsfunktion modulo
Ausgabe: Ein nicht-trivialer Faktor von oder eine Fehlermeldung
- x ← 2, y ← x; d ← 1
- Solange d = 1:
- x ← f(x)
- y ← f(f(y))
- d ← ggT(|x − y|, n)
- Wenn 1 < d < n, dann d zurückgeben.
- Falls d = n, dann „Fehler“ ausgeben.
Anmerkung: Dieser Algorithmus liefert für alle , die nur durch 1 und sich selbst teilbar sind, eine Fehlermeldung zurück. Allerdings kann auch für die anderen eine Fehlermeldung zurückgeliefert werden. In diesem Fall wählt man eine andere Funktion und versucht es erneut.
Ist das Ergebnis eine Zahl, so ist diese wirklich auch ein Teiler und damit ein korrektes Ergebnis, wobei dieses im Allgemeinen nicht zwingend eine Primzahl sein muss.
Für wählt man ein Polynom mit einem ganzzahligen Koeffizienten. Eine übliche Funktion für diesen Algorithmus hat folgende Form:
Abschätzung der Laufzeit[Bearbeiten | Quelltext bearbeiten]
Die Zahlenfolgen und können als Pseudo-Zufallsfolgen angesehen werden. Falls ein Zahlenwert erneut auftritt, wiederholen sich zwangsläufig die folgenden Werte. Es können bis zu Werte angenommen werden (bei quadratischem wie oben: bis zu Werte). Der Erwartungswert für die Länge eines Zyklus beträgt . Die Tatsache, dass weit weniger als Berechnungen erforderlich sind, wird zuweilen Geburtstagsparadoxon genannt.
Der ungünstigste Fall tritt ein, wenn ein Produkt von zwei Primzahlen gleicher Länge ist. Der Algorithmus terminiert dann nach O(n1/4 polylog(n)) Schritten mit einer Wahrscheinlichkeit von . Die Methode ist gut geeignet, um Zahlen mit mehreren kleineren Faktoren zu faktorisieren. Der Algorithmus kann in der gleichen Zeit (mit hoher Wahrscheinlichkeit) eine Zahl mit doppelt so vielen Stellen wie die Probedivision faktorisieren. Der Algorithmus arbeitet exponentiell in der Länge der Eingabe und ist damit asymptotisch langsamer als das Quadratische Sieb und das Zahlkörpersieb.
Zahlenbeispiel[Bearbeiten | Quelltext bearbeiten]
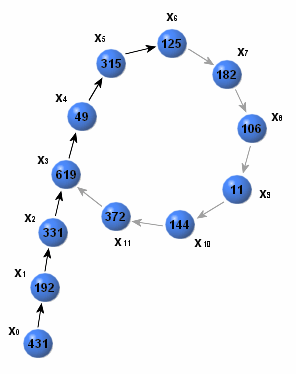
1. Beispiel
Gesucht seien die Faktoren der Zahl . Wir verwenden die Funktion und den Startwert :
| mit | |||
| 1 | 192 | 331 | 1 |
| 2 | 331 | 49 | 1 |
| 3 | 619 | 125 | 19 |
| 4 | 49 | 106 | 19 |
| 5 | 315 | 144 | 19 |
| 6 | 125 | 619 | 19 |
| 7 | 182 | 315 | 19 |
| 8 | 106 | 182 | 19 |
| 9 | 11 | 11 | 703 |
| 10 | 144 | 372 | 19 |
| 11 | 372 | 49 | 19 |
| 12 | 619 | 125 | 19 |
Damit ist die Primfaktorzerlegung von gefunden.
2. Beispiel
| mit | |||
| 1 | 8 | 68 | 1 |
| 2 | 68 | 277 | 209 |
| 3 | 1911 | 2367 | 19 |
| 4 | 277 | 68 | 209 |
| 5 | 657 | 277 | 19 |
| 6 | 2367 | 2367 | 2717 |
| 7 | 239 | 68 | 19 |
| 8 | 68 | 277 | 209 |
Dieses Beispiel zeigt, dass der gefundene Faktor nicht zwingend eine Primzahl sein muss. Der hier gefundene Faktor ist .
Faktorisierungen[Bearbeiten | Quelltext bearbeiten]
Mit der beschriebenen Methode konnte 1980 die Fermat-Zahl
faktorisiert werden. bezeichnet dabei eine (Prim)Zahl mit 62 Stellen, von der erst später bewiesen wurde, dass es sich bei ihr um eine Primzahl handelt.
Implementierungen[Bearbeiten | Quelltext bearbeiten]
Die Rho-Methode ist unter dem Namen rho_factorize() Bestandteil der Funktionsbibliothek des Programms ARIBAS von Otto Forster.
Literatur[Bearbeiten | Quelltext bearbeiten]
- A Monte Carlo Method for Factorization, J.M.Pollard, BIT 15 (1975) 331–334
- An Improved Monte Carlo Factorization Algorithm, R.P.Brent, BIT 20 (1980) 176–184
- Otto Forster: Algorithmische Zahlentheorie. Vieweg, 1996, ISBN 3-528-06580-X



















































