Polylogarithmus
Der Polylogarithmus ist eine spezielle Funktion, die durch die Reihe
definiert ist. Für geht der Polylogarithmus in den gewöhnlichen Logarithmus über:
In den Fällen und spricht man entsprechend von Dilogarithmus bzw. Trilogarithmus. Die Definition gilt für komplexe und mit . Durch analytische Fortsetzung lässt sich diese Definition auf weitere ausdehnen.
In den wichtigsten Anwendungsfällen ist eine natürliche Zahl. Für diese Fälle kann man den Polylogarithmus rekursiv durch
definieren, wonach der Dilogarithmus ein Integral des Logarithmus ist, der Trilogarithmus ein Integral des Dilogarithmus und so fort. Für negative ganzzahlige Werte von lässt sich der Polylogarithmus durch rationale Funktionen ausdrücken.
Der Polylogarithmus taucht beispielsweise im Zusammenhang mit der Fermi-Dirac-Verteilung und der Bose-Einstein-Verteilung auf. Zudem kann mit ihm im hexadezimalen Zahlensystem eine beliebige Stelle von polylogarithmischen Konstanten (z. B. ) einzeln berechnet werden.
Funktionswerte und Rekursionen[Bearbeiten | Quelltext bearbeiten]

Funktionswerte mit Index unter Zwei[Bearbeiten | Quelltext bearbeiten]
Einige explizite Funktionsterme für spezielle ganzzahlige Werte von :
Formal kann man mit der (für alle divergierenden) Reihe definieren. Obwohl diese Reihe nicht konvergiert, kann diese Definition zum Beweis von Funktionalgleichungen (im Ring der formal definierten Laurent-Reihen) verwendet werden.
Für alle ganzzahligen nichtpositiven Werte vom Index kann der Polylogarithmus als Quotient von Polynomen geschrieben werden. In diesen Fällen ist er also eine rationale Funktion.
Funktionswerte mit positivem Index[Bearbeiten | Quelltext bearbeiten]
Es gilt
und
Der Buchstabe stellt dabei die Riemannsche Zetafunktion und der Buchstabe die Dirichletsche Etafunktion[1] dar.
Für größeres sind keine weiteren derartigen Formeln bekannt.
Die zwei bekanntesten Werte des Dilogarithmus und somit des Polylogarithmus mit Indexzahl Zwei sind die folgenden Werte:
Diese beiden Werte gehen direkt aus der folgenden Integralidentität für den Dilogarithmus hervor:
Durch das Einsetzen der Werte sowie erscheinen direkt die soeben genannten Funktionswerte.
Und die nun gezeigte Formel geht wiederum aus dieser Areatangens-Hyperbolicus-Cardinalis-Formel durch Bildung der Ursprungsstammfunktion bezüglich hervor:
Für die drei kleinsten positiven Werte vom Index sind im Folgenden die Funktionswerte an der Stelle des inneren Klammerwertes angegeben:
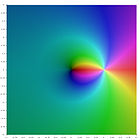
Die folgende Bildertafel zeigt die komplexen Ebenendiagramme für die Polylogarithmen.
Die erste Zeile zeigt die Diagramme für die Polylogarithmen von negativem Index und Nullindex und die zweite Zeile diejenigen von positivem Index:
 |
 |
 |
 |
 |
 |
 | |
Ableitung[Bearbeiten | Quelltext bearbeiten]
Die Ableitung der Polylogarithmen sind wieder Polylogarithmen:
Integraldarstellung[Bearbeiten | Quelltext bearbeiten]
Der Polylogarithmus lässt sich für alle komplexen durch
Auf der Abel-Plana-Summenformel basiert diese für den gesamten komplexen Raum gültige Gleichung.
mit Hilfe des Integralausdrucks für die Lerchsche Zeta-Funktion darstellen. Dabei ist die unvollständige Gammafunktion der unteren Grenze.
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Mehrdimensionale Polylogarithmen[Bearbeiten | Quelltext bearbeiten]
Die mehrdimensionalen Polylogarithmen sind folgendermaßen definiert:[2]
Lerchsche Zeta-Funktion[Bearbeiten | Quelltext bearbeiten]
Der Polylogarithmus ist ein Spezialfall der transzendenten Lerchschen Zeta-Funktion:
Nielsens verallgemeinerte Polylogarithmen[Bearbeiten | Quelltext bearbeiten]
Nielsen fand folgende Verallgemeinerung für den Polylogarithmus:[3]
Es gilt:
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Alexander Goncharov: Polylogarithms in arithmetic and geometry. (PDF; 228 kB) In: Proceedings of the International Congress of Mathematicians (Zürich, 1994). Birkhäuser, Basel 1995, Vol. 1, 2, S. 374–387.
- Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions. Dover Publications, New York 1964, ISBN 978-0-486-61272-0, Abs. 27.7.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Dilogarithm, Trilogarithm und Polylogarithm. In: MathWorld (englisch).
- David H. Bailey, David J. Broadhurst: A seventeenth-order polylogarithm ladder. arxiv:math.CA/9906134
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Eric W. Weisstein: Dirichlet Eta Function. In: MathWorld (englisch).
- ↑ Eric W. Weisstein: Multidimensional Polylogarithms. In: MathWorld (englisch).
- ↑ Eric W. Weisstein: Nielsen Generalized Polylogarithm. In: MathWorld (englisch).

















































