Quantenschaltung

Mit Quantenschaltung wird in der Quanteninformatik ein abstraktes Modell für Quantencomputer bezeichnet. Die darin stattfindende Berechnung ist eine Folge von Operationen an Quantengattern, Quantenmessungen und Initialisierungen von Qubits welche reversible Transformationen auf dem quantenmechanischen Gegenstück eines n-Bit Registers durchführt, das auch n-Qubit-Register (oder Quantenregister) bezeichnet wird.

Algorithmen und Anwendungen, die quantenmechanische Ressourcen nutzen, können einfach und effizient in der Sprache von „Quantenschaltkreisen“ geschrieben werden. Ein Quantenschaltkreis ist eine Rechenroutine, die aus kohärenten Quantenoperationen auf Quantendaten besteht, wie sie in Qubits gehalten werden, und parallel dazu ablaufenden klassischen Echtzeit-Berechnungen.

Darstellung der Quantenschaltungen

Quantenschaltung für den Bit-Flip-Code: Zwei CNOT-Gatter kodieren das Qubit. Die letzten drei Gatter (2× CNOT, 1× Toffoli) dekodieren es wieder.

Die Notation für Quantengatter wurde von den Begründern der Quanteninformatik, daruntern Adriano Barenco, Charles Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin und Harald Weinfurter entwickelt.

Die Notation der Schaltkreise wurde 1986 von Richard Feynman eingeführt.

Quantenalgorithmen sind in einem Diagramm leichter zu verstehen als in der entsprechenden ausgeschriebenen Matrixdarstellung. Quantenschaltkreise werden ähnlich dargestellt, wie klassische Schaltkreise, jedoch haben die Quantenschaltkreise, wie die Quantenbausteine aus denen sie bestehen, für n Eingänge immer auch n Ausgänge. Sie beschreiben die Zustandstransformationen durch, die sich durch die Hintereinanderausführung der Quantenbausteine ergibt.

In einem Schaltungsdiagramm stellt jede durchgezogene Linie ein Qubit oder allgemeiner ein Qubit-Register dar. Gemäß der Konvention ist die oberste Zeile das Qubit (oder Register) 1 und die restlichen Elemente werden dann aufsteigend nummeriert.

In einer Quantenschaltung fließt die Zeit von links nach rechts. Quantengatter sind in chronologischer Reihenfolge angeordnet, wobei das äußerste linke Gatter zuerst auf die Qubits angewendet wird. Der Quantenzustand der Qubits propagiert von links nach rechts durch die einzelnen Gatter des Diagramms und wird durch die Gatter verändert.

Die Leitungen in einem Quantenschaltkreis lassen sich als die einzelnen Qubits interpretieren, wobei der Zustand einer Leitung dem Zustand eines Qubits entspricht. Der Gesamtzustand aller Leitungen ergibt sich jedoch auf Grund der Besonderheiten der Quantenschaltkreise nicht unbedingt aus den Teilzuständen der Leitungen.

Jede horizontale Linie oder Draht in einer Schaltung stellt somit ein Qubit dar, wobei das linke Ende des Drahtes die ursprünglichen Quantendaten (Input) darstellt und das rechte die Quantendaten, die durch die Berechnung des Quantenschaltkreises erzeugt werden (Output). Operationen auf Qubits werden durch Boxen (Gatter) dargestellt, die auf diesen Drähten platziert sind.

Zusammenfassen zu Komplexen

Einzelne Gatterschaltungen lassen sich zu einem Block zusammenfassen und in einer Art Blockdiagramm darstellen. Die vielleicht hilfreichste Eigenschaft dieser abstrakten Schaltungsdiagramme ist, dass sie eine allgemeine Beschreibung komplexer Quantenalgorithmen ermöglichen, ohne elementare Gates darstellen zu müssen. So können Sie eine Vorstellung vom Datenfluss für einen großen Quantenalgorithmus erhalten, ohne alle Details der einzelnen Unterroutinen innerhalb des Algorithmus verstehen zu müssen.

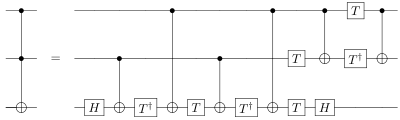
Beispiel: Darstellung eines Toffoli-Gatters

Quantenschaltungen werden benützt, um die Realisation komplexer Quantengatter aus einfachen Gattern und Quantenbausteinen darzustellen.

Konstruktion eines Toffoli-Gatters aus ein Ein-Qubit-Gattern (T und Hadamard) und sechs CNOT-Gattern.

Schaltsymbol für das Toffoli-Gatter

Legende

	Hadamard-Gatter
	CNOT-Gatter
	T-Gatter

Reversible Logikgatter

Im klassischen Computer sind Logikgatter mit mehr als einem Eingang (alle außer dem Nicht-Gatter) und einem Ausgang nicht reversibel. Beispielsweise kann man für ein Und-Gatter aus dem Ausgangs-Bit 0 nicht ableiten, ob die Eingangswerte 0,1 oder 1,0 oder 0,0 waren. Es ist jedoch auch in einem klassischen Computer theoretisch möglich, für Eingangswerte beliebiger Länge reversible Gatter zu konstruieren. Ein reversibles Gatter ist eine umkehrbare Funktion, die n-Bit auf n-Bit abbildet, wobei das n-Bit-Datum eine Zeichenkette der Länge n mit den Bits x₁,x₂, …,x_n.

Das n-Bit-Datum ist Element der Menge {0,1}ⁿ. Diese enthält 2ⁿ Elemente.

Ein reversibles n-Bit-Gatter ist eine bijektive Abbildung f aus der Menge {0,1}ⁿ von n-Bit-Daten auf sich selbst.

Ein Beispiel für ein derartiges Gatter f ist eine Abbildung, welche das erste Bit negiert.

Aus praktischen Erwägungen werden hier nur Gatter für kleine Werte von n betrachtet, also n = 1, n = 2 oder n = 3. Diese Gatter können leicht als Tabellen beschrieben werden. Ein Beispiel n = 2 ist das kontrollierte Nicht-Gatter, das Toffoli-Gatter und das Fredkin-Gatter.

Für die Betrachtung von Quantengattern muss man die quantenmechanische Ersetzung eines n-Bit-Datums definieren.

Die quantisierte Version eines klassischen n-Bit-Zustandsraums {0,1}ⁿ ist

$H_{\operatorname {QB} (n)}=\ell ^{2}(\{0,1\}^{n}).$

Dies ist definitionsgemäß der Raum von komplexwertigen Funktionen von {0,1}ⁿ und ist ein Prähilbertraum. Dieser Raum kann auch als Überlagerung von klassischen Bit-Zeichenketten betrachtet werden. Man beachte, dass H_QB(n) ein Vektorraum über den komplexen Zahlen der Dimension 2ⁿ ist.

Die Elemente dieses Raums werden n-Qubit genannt.

Beschreibt x₁,x₂, …,x_n in der Bra-Ket-Notation die klassische Bit-Zeichenkette, dann ist

$|x_{1},x_{2},\cdots ,x_{n}\rangle \quad$

ein spezielles n-Qubit korrespondierend zu der Funktion, die die klassische Bit-Zeichenkette auf 1 abbildet und alle anderen Zeichenketten auf 0. Diese 2ⁿ speziellen n-Qubits sind die Berechnungszustandsbasis der Funktion. Alle n-Qubits sind komplexe Linearkombinationen dieser Basis.

Für ein Quantengatter benötigt man eine spezielle Art einer reversiblen Funktion, nämlich eine unitäre Abbildung. Diese ist eine Abbildung auf H_QB(n), bei der die Skalarprodukte erhalten bleiben.

Ein reversibles n-Qubit Quantengatter ist eine unitäre Abbildung U aus dem Raum H_QB(n) auf sich selbst.

Wiederum ist nur die Unitäre Abbildungen U für kleine n von Interesse. Aus einem reversiblen n-Bit-Gatter f lässt sich ein reversibles n-Bit-Quantengatter W_f bilden, das wie folgt definiert ist:

$W_{f}(|x_{1},x_{2},\cdots ,x_{n}\rangle )=|f(x_{1},x_{2},\cdots ,x_{n})\rangle .$

Man beachte, das W_f die Berechnungszustandsbasis permutiert.

Von speziellem Interesse ist das 2-Qubit-CNOT-Gatter W_CNOT. Mit diesem Gatter wird deutlich, dass es über die Permutation der Basis hinaus viele weitere Quanten-Gatter gibt. Beispielsweise ist eine Verschiebung der Phase durch Multiplikation mit folgender unitärer Matrix ebenfalls zulässig:

$U_{\theta }={\begin{bmatrix}e^{i\theta }&0\\0&1\end{bmatrix}},$

also

$U_{\theta }|0\rangle =e^{i\theta }|0\rangle \quad U_{\theta }|1\rangle =|1\rangle .$

Reversible Schaltungen

→ Hauptartikel: Reversibles Computing

Wiederum betrachten wir zunächst die reversible klassische Berechnung. Grundsätzlich gibt es keinen Unterschied zwischen einer reversiblen n-Bit Schaltung und einem reversiblen n-Bit-Gatter. Es ist lediglich eine umkehrbare Funktion im Raum der n-Bit-Daten. Wie bereits im vorherigen Abschnitt beschrieben, möchte man aus praktischen Erwägungen eine kleine Anzahl reversibler Gatter haben, die zu einer reversiblen Schaltung zusammengesetzt werden können. Der Zusammenbau einer Schaltung wird an folgendem Beispiel deutlich. Angenommen man hat ein reversibles n-Bit-Gatter f und ein reversible m-Bit-Gatter g. Zusammenbau heißt, eine neue Schaltung herzustellen, indem man eine Teilmenge der k < n der Ausgänge von f mit einer Teilmenge k der Eingänge von g verbindet, wie im Bild unten dargestellt. In diesem Bild ist n = 5, k = 3 und m = 7. Die resultierende Schaltung ist ebenfalls reversibel und verarbeitet n + m − k Bits.

Im Folgenden wird diese Schema als klassischer Verbund bezeichnet. Beim Zusammenbau dieser reversibler Maschinen ist es wichtig, dass die Zwischenstufen ebenfalls reversibel sind. Mit dieser Bedingung wird sichergestellt, dass sich innerhalb der Maschine die Entropie nicht erhöht (Abfall). Damit ist es möglich zu zeigen, dass das Toffoli-Gatter ein Quantengatter ist. Das bedeutet, dass zu einer beliebigen reversiblen klassischen n-Bit-Schaltung h in oben beschriebener Weise ein klassischer Verbund aus Toffoli-Gattern eine n+m-Bit-Schaltung f erzeugen werden kann, so dass gilt.

$f(x_{1},\ldots ,x_{n},\underbrace {0,\dots ,0} )=(y_{1},\ldots ,y_{n},\underbrace {0,\ldots ,0} )$

Darin sind die Bereiche oberhalb der spitzen Klammern m 0-Eingaben und es gilt

$(y_{1},\ldots ,y_{n})=h(x_{1},\ldots ,x_{n})$.

Man beachte, dass das Endergebnis immer eine Kette von m Nullen als Hilfbits enthält. Es wird an keiner Stelle Abfall produziert, so dass die Berechnung tatsächlich im physikalischen Sinne keine Entropie erzeugt. Daraus folgt sofort, dass jede Funktion f (ob bijektiv oder nicht) durch eine Schaltung von Toffoli-Gattern simuliert werden kann. Wenn die Abbildung jedoch nicht injektiv ist, muss die Simulation an irgendeiner Stelle Abfall produzieren, z. B. beim letzten Schritt.

Für Quantenschaltungen kann eine ähnliche Verbindung von Qubit-Gattern definiert werden. Diese lässt sich mit dem klassischen Verbund oben assoziieren, indem man anstelle von f ein n-Qubit-Gatter U und statt g das m-Qubit-Gatter W verwendet. Daraus erhält man eine reversible Quantenschaltung, wie in der folgenden Abbildung dargestellt.

Es lässt sich leicht zeigen, dass sich durch Verbindung der Gatter eine unitäre Abbildung auf dem n+m−k-Qubit-Raum entsteht. Außerdem sei noch angemerkt, dass in realen Quantencomputern die physikalische Verbindung zwischen den Gattern eines der Hauptprobleme darstellt, da sie eine der Stellen ist, wo Dekohärenz auftreten kann.

Außerdem bilden einige Mengen wohlbekannter Gatter universelle Gatter. So ist das oben erwähnte Einzel-Qubit-Phasengatter U_Θ für sinnvolle Werte von Θ zusammen mit dem 2-Qubit-CNOT-Gatter W_CNOT universell. Allerdings ist die Universalität im Falle der Quantenberechnung etwas schwächer. Jede reversible n-Qubit-Schaltung kann beliebig nahe durch diese beiden elementaren Gatter approximiert werden. Man beachte dass es überabzählbar viele mögliche Einzel-Qubit-Phasengatter gibt (eines für jeden möglichen Winkel Θ). Damit können überabzählbar viele dieser Gatter nicht durch endliche Schaltungen aus {U_?, W_CNOT} konstruiert werden.

Quantenberechnungen

Da viele wichtige numerische Probleme sich auf die Berechnung einer unitären Transformation U auf einem endlich-dimensionalen Raum reduzieren lassen (als prominenteste Beispiel sei die Diskrete Fourier-Transformation genannt), könnte man erwarten, das man eine Quantenschaltung für die Transformation U bauen kann. Im Prinzip muss man nur einen n-Qubit-Zustand Ψ als zugehörige Superposition der Berechnungszustandsbasis für den Eingang präparieren und dann die Ausgänge von UΨ messen. Leider gibt es damit zwei Probleme:

• Man kann die Phase von Ψ nicht für jeden Basiszustand messen. Daher gibt es keine Möglichkeit, das vollständige Ergebnis zu messen. Dies liegt in der Natur der quantenmechanischen Messung.
• Es ist nicht möglich, den Eingangszustand Ψ effizient zu präparieren.

Trotzdem können Quantenschaltungen für die diskrete Fouriertransformation als Zwischenschritt in anderen Quantenschaltungen benutzt werden. Die Verwendung ist jedoch etwas komplizierter. Tatsächlich sind Quantenberechnungen probabilistisch.

Es wird nun ein mathematisches Modell für die Simulation von probabilistischen statt klassischen Berechnungen erstellt. Man betrachte eine r-Qubit-Schaltung U mit dem Registerraum H_QB(r). Damit ist U eine unitäre Abbildung

$H_{\operatorname {QB} (r)}\rightarrow H_{\operatorname {QB} (r)}.$

Um diese Schaltung mit der klassischen Abbildung von Bit-Zeichenketten zu assoziieren, spezifiziert man

• Ein Eingangsregister X = {0,1}^m von m (klassischen) Bits.
• Ein Ausgangsregister Y = {0,1}ⁿ von n (klassischen) Bits.

Der Inhalt x = x₁, …, x_m des klassischen Eingangsregisters wird irgendwie für die Initialisierung des Qubit-Registers verwendet. Idealerweise wird das mit der Berechnungszustandsbasis gemacht.

$|{\vec {x}},0\rangle =|x_{1},x_{2},\cdots ,x_{m},\underbrace {0,\dots ,0} \rangle$

Dabei gibt es unter der Klammer r − m 0-Eingänge.

Dennoch ist die perfekte Initialisierung absolut unrealistisch. Man nehme daher an, dass die Initialisierung ein Mischzustand ist, der durch den Dichteoperator S gegeben ist. Dieser ist in einer geeigneten Metrik dem idealen Eingangszustand sehr ähnlich, z. B.

$\operatorname {Tr} \left({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |}\right)\leq \delta$

Ebenso steht der Ausgangsregister-Raum mit dem Qubit-Register über die durch ein Y angenäherte Observable A in Beziehung. Es sei angemerkt, dass Observable in der Quantenmechanik üblicherweise durch projizierte Größenwerte ausgedrückt werden. Wenn die Variable diskret ist, dann reduziert sich der projizierte Größenwert auf eine Familie {E_λ}. Dabei ist λ ein Parameter über einer abzählbaren Menge. Analog kann eine Observable Y mit einer Familie von paarweisen orthogonalen Projektionen {E_y} indexiert durch Y assoziiert werden. Damit ist

$I=\sum _{y\in Y}\operatorname {E} _{y}.$

Zu einem gegebenen Mischzustand S korrespondiert ein Wahrscheinlichkeitsmaß für Y

$\operatorname {Pr} \{y\}=\operatorname {Tr} (S\operatorname {E} _{y})$

Die Funktion F:X → Y wird durch die Schaltung U:H_QB(r) → H_QB(r) innerhalb von ε berechnet genau dann, wenn für alle Bitzeichenketten x der Länge m gilt

$\left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle =\left\langle \operatorname {E} _{F(x)}U(|{\vec {x}},0\rangle ){\big |}U(|{\vec {x}},0\rangle )\right\rangle \geq 1-\epsilon$

Damit gilt

$\left|\operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)-\left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle \right|\leq \operatorname {Tr} ({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |})\|U^{*}\operatorname {E} _{F(x)}U\|\leq \delta$

so dass

$\operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)\geq 1-\epsilon -\delta$

Satz. Wenn $\epsilon +\delta <{\frac {1}{2}}$, dann kann die Wahrscheinlichkeitsverteilung

$\operatorname {Pr} \{y\}=\operatorname {Tr} (SU^{*}\operatorname {E} _{y}U)$

auf Y verwendet werden, um F(x) bei hinreichend vielen Stichproben mit einer beliebig kleinen Fehlerwahrscheinlichkeit zu bestimmen. Nimmt man k unabhängigen Stichproben aus der Wahrscheinlichkeitsverteilung Pr auf Y, dann ist die Wahrscheinlichkeit, dass der Wert F(x) mehr als k/2-mal gemessen wird mindestens

$1-e^{-2\gamma ^{2}k}$

wobei $\gamma ={\frac {1}{2}}-\epsilon -\delta$. Dies folgt aus der Chernoff-Ungleichung.

Siehe auch

• Quantengatter
• Liste der Quantengatter
• Quantenschaltkreis der Quanten-Fouriertransformation

Literatur

• Eli Biham, Gilles Brassard, Dan Kenigsberg, Tal Mor: Quantum computing without entanglement. In: Theoretical Computer Science. Band 320, Nr. 1, 2004, S. 15–33, doi:10.1016/j.tcs.2004.03.041, arxiv:quant-ph/0306182. 
• M.H. Freedman, A. Kitaev, M.J. Larsen, Z. Wang: Topological quantum computation. In: Bulletin of the AMS. Band 40, Nr. 1, 2003, S. 31–38 (ams.org [PDF]). 
• Mika Hirvensalo: Quantum Computing. Springer, Berlin 2000, ISBN 3-540-66783-0. 
• M. A. Nielsen, I. L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge MA 2010, ISBN 978-1-107-00217-3 (wordpress.com [PDF]). 

• M. Homeister: Vom Quantenregister zum Quantenschaltkreis. In: Quantum Computing verstehen: Grundlagen, Anwendungen, Perspektiven. Springer/Vieweg, Wiesbaden 2022, ISBN 978-3-658-36433-5, S. 67–99 (springer.com [PDF]). 

Weblinks

• Quantum circuit on arxiv.org (englisch)
• Q-circuit ist eine Makro-Bibliothek zum Zeichnen von Quantenschaltungen in LaTeX.
• Dagmar Bruß: Quantenschaltkreise - ein erster Eindruck Video Vorlesung