Rake Receiver
Als Rake-Receiver, auch Rake-Empfänger, bezeichnet man Empfangsgeräte für digitale Signale, die auf den Mehrwegempfang ausgelegt sind. Ein Rake-Empfänger besteht aus mehreren Teilempfängern, die das Empfangssignal zeitlich hintereinander empfangen und auswerten. Durch die Aneinanderreihung der einzelnen Teilempfänger ergibt sich eine Struktur, die in der schematischen Darstellung wie ein Rechen (engl. Rake) aussieht und dieser Empfangsstruktur ihren Namen gibt.
Anwendungen findet der Rake-Empfänger insbesondere bei mobil genutzten Funkübertragungen, welche auf dem Codemultiplexverfahren (CDMA) bzw. Wideband CDMA basieren. Dies sind beispielsweise Empfänger für die Mobilfunkstandards wie UMTS, CDMA2000 oder bei dem Wireless Local Area Network (WLAN).
Funktionsprinzip[Bearbeiten | Quelltext bearbeiten]
Der Rake-Empfänger ist durch Korrelation in der Lage, aus einem Signal, das sich wegen des Mehrwegeempfanges über mehrere Pfade ausbreitet und sich zeitlich versetzt überlagert, gezielt Signalkomponenten herauszugreifen und diese konstruktiv, das heißt mit einer Verbesserung des Signal/Rauschleistungsverhältnisses, zu empfangen.
Damit eine Entzerrung der Mehrwegeausbreitung mit einem Rake-Receiver möglich ist, muss das zu übertragende Datensignal vor der Modulation mit einer in den meisten Fällen antipodalen (bipolaren) Spreizsequenz multipliziert werden. Durch das eingesetzte Direct Sequence Spread Spectrum (DSSS) wird die Bandbreite gespreizt. Die empfängerseitige genaue Kenntnis der Spreizsequenz und ihres Startzeitpunkts ermöglicht dann eine Rückgewinnung der Komponenten des Sendesignals, die sich über Pfade mit unterschiedlichen Laufzeiten ausgebreitet haben. Hierbei macht man sich die Eigenschaften der Autokorrelation und der Kreuzkorrelation der verwendeten Spreizsequenz zu Nutze.
Prinzip der Bandspreizung[Bearbeiten | Quelltext bearbeiten]
Das Datensignal sei ein bipolares Datensignal, das aus rechteckförmigen Impulsen besteht, also
- mit und
Die Symboldauer des Datensignals ist damit . Dieses Sendesignal nimmt eine gewisse spektrale Bandbreite von in Anspruch. Diese ergibt sich aus der Fouriertransformation des Datensignals. Wegen des qualitativ gegenläufigen Zusammenhangs von Symboldauer und Spektralflächenbandbreite, der zumindest bei gleich wahrscheinlichen Sendebits auftritt, erscheint es unmittelbar einleuchtend, dass die Bandbreitenbelegung durch unmittelbar gegenläufig mit der Symboldauer verknüpft ist. Die Multiplikation mit der ebenfalls bipolaren Spreizsequenz
- mit und und weiterhin
führt zu dem Signal
Weil nun die Symboldauer des Datensignals ein ganzzahliges Vielfaches der Symboldauer der Spreizsequenz ist, ist anschaulich sofort klar, dass in höhere Frequenzen, als in auftreten. Die Symboldauer der Spreizsequenz heißt Chipdauer. Ein Chip beschreibt einen Zustand, also ein Symbol, der Spreizsequenz. Eine genauere Analyse verrät, dass das von belegte Frequenzband um den Faktor breiter geworden ist. Aus diesem Grund nennt man die Größe , die der Länge des Spreizcodes entspricht, Spreizfaktor. Eine genauere Beschreibung des Prinzips der spektralen Spreizung ist im Artikel Codemultiplexverfahren zu finden.
Anforderungen an Codesequenzen[Bearbeiten | Quelltext bearbeiten]
Rake-Receiver eignen sich besonders zur Entzerrung von sogenannten Makropfaden. Ein Makropfad zeichnet sich dadurch aus, dass die Laufzeit des Signals auf dem jeweiligen Pfad sehr viel größer ist als die Chipdauer. Wesentliche Eigenschaft der verwendeten Spreizsequenz bei der Einzelnutzerübertragung ist ihre Autokorrelationseigenschaft. Anschaulich beschreibt die Autokorrelation die lineare Ähnlichkeit eines Signals zu sich selbst, wenn das Signal um eine bestimmte Zeit verschoben wird. Siehe hierzu den Artikel Autokorrelation.
Eine geeignete Spreizsequenz hat idealerweise eine scharfe und periodische Autokorrelationsfunktion. Scharf bedeute hierbei, dass die periodische Autokorrelationsfunktion der Spreizsequenz bei Verschiebungen, die einem ganzzahligen Vielfachen von entsprechen ihren Maximalwert annimmt, aber die lineare Ähnlichkeit der Spreizsequenz zu sich selbst, bereits bei Verschiebungen von verschwunden ist.
Spreizsequenzen, die diese Anforderung theoretisch perfekt erfüllen sind Signale, die sogenannten M-Sequenzen, welche sich systematisch mit Hilfe von Schieberegistern gewinnen lassen. Man sagt: Zwei unterschiedliche, um mindestens eine Chipdauer unterschiedlich verzögerte M-Sequenzen sind exakt orthogonal zueinander. Diese Eigenschaft zusammen mit der Tatsache, dass die Multiplikation einer (bipolaren) Spreizsequenz mit sich selbst, also gleichverzögert, zu jedem Zeitpunkt genau 1 ergibt ist die Grundlage der Funktionsweise des Rake-Receivers.
Beispiel der Zweiwegeausbreitung[Bearbeiten | Quelltext bearbeiten]
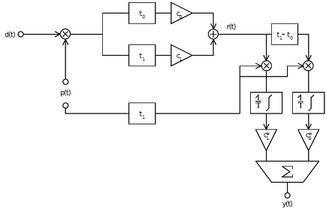
In diesem Abschnitt soll die Übertragungskette des Datensignals d(t), das Sendeseitig mit der Spreizsequenz p(t) gespreizt wird, am Beispiel von Zweiwegeausbreitung dargestellt werden. Das Signal p(t) erfülle zumindest näherungsweise die Forderung nach einer scharfen periodischen Autokorrelationsfunktion. Das Szenario ist in nebenstehenden Bild dargestellt.
Die Laufzeit sei größer als die Laufzeit . Der Rake-Receiver mit zwei Korrelatoren (Rake-Fingern) ist im rechten Teil der Graphik vertikal angeordnet, während der Übertragungskanal als horizontal angeordnetes Laufzeitsystem zu erkennen ist. Betrachtet werden nun die beiden Rake Finger und die in ihnen stattfindenden Operationen:
Im ersten Finger wird das Empfangssignal zunächst mit der um verzögerten Spreizsequenz gewichtet und anschließend über eine Symboldauer des Datensignals integriert (gemittelt). Anschließend erfolgt die Multiplikation mit der Kanalspezifischen Verstärkung . Das Produkt von und sei eine von Null verschiedene reelle Zahl, welche von der An- und Abwahl, so wie der sinnvollen Gewichtung der Rake-Finger abhängt. Dann gilt für das Ausgangssignal des ersten Rake-Fingers:
Wegen der oben geforderten Korrelationseigenschaften der Spreizsequenz ist aber
- und .
Damit gilt:
Während im zweiten Rake-Finger das Empfangssignal zunächst um die Laufzeitdifferenz auf beiden Pfaden verzögert wird, was unmittelbar sinnvoll erscheint, wenn man bedenkt, dass die beiden Signalanteile, die sich über die beiden Kanalpfade mit den Verzögerungen und ausbreiten, für eine konstruktive Überlagerung Phasenrichtig addiert werden müssen. Es gilt dann:
Wegen der geforderten Korrelationseigenschaften der Spreizsequenz gilt analog zum ersten Rake-Finger:
- und .
und damit für das Ausgangssignal des zweiten Rake-Fingers:
Das Datensignal lässt sich damit aus empfangsseitig zurückgewinnen.
Literatur[Bearbeiten | Quelltext bearbeiten]
- John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Prentice-Hall, 2002, ISBN 0-13-095007-6.
- C. Lüders: Mobilfunksysteme. Vogel Buchverlag, Würzburg 1996.



![{\displaystyle g_{r}(t)={\begin{cases}1&t\in [{\frac {-T_{d}}{2}};{\frac {T_{d}}{2}}]\\0&{\text{sonst.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07889dbafaf304225968c9fe92f5312a90b658c7)




![{\displaystyle g_{p}(t)={\begin{cases}1&t\in [{\frac {-T_{c}}{2}};{\frac {T_{c}}{2}}]\\0&{\text{sonst.}}\end{cases}}:}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b758ac9806ba6d51d1fb02bf929a09e50c0f8586)










![{\displaystyle {\begin{aligned}y_{1}(t)&={\frac {c_{1}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}[c_{0}\cdot d(t-t_{0})\cdot p(t-t_{0})+c_{1}\cdot d(t-t_{1})\cdot p(t-t_{1})]\cdot p(t-t_{1})\,\mathrm {d} t\\&={\frac {c_{1}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}[c_{0}\cdot d(t-t_{0})\cdot p(t-t_{0})]\cdot p(t-t_{1})\,\mathrm {d} t+{\frac {c_{1}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}[c_{1}\cdot d(t-t_{1})\cdot p(t-t_{1})]\cdot p(t-t_{1})\,\mathrm {d} t\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf7cac31c11df03107d3139eb7e7b426f361f438)



![{\displaystyle {\begin{aligned}y_{2}(t)&={\frac {c_{0}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}[c_{0}\cdot d(t-t_{0}-t_{1}+t_{0})\cdot p(t-t_{0}-t_{1}+t_{0})+c_{1}\cdot d(t-2t_{1}+t_{0})\cdot p(t-2t_{1}+t_{0})]\cdot p(t-t_{1})\,\mathrm {d} t\\&={\frac {c_{0}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}c_{0}\cdot d(t-t_{1})\cdot p(t-t_{1})\cdot p(t-t_{1})\,\mathrm {d} t+{\frac {c_{0}^{*}}{T_{\mathrm {d} }}}\int \limits _{0}^{T_{\mathrm {d} }}c_{1}\cdot d(t-2t_{1}+t_{0})\cdot p(t-2t_{1}+t_{0})\cdot p(t-t_{1})\,\mathrm {d} t\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f1f36e8c3b0b6120da5a5483a86bc80cc47bb18)


