Signalflussgraph
Ein Signalflussgraph ist eine Darstellung der Signalverarbeitung in einem System durch einen gerichteten, gewichteten Graphen. Die Knoten dieses Graphen sind dabei kleine Bearbeitungseinheiten, die die eingehenden Signale in einer bestimmten Form verarbeiten und das Ergebnis dann an alle ausgehenden Kanten senden[1].
Vom Signalflussplan unterscheiden sie sich durch die Bedeutung der Knoten und Kanten.
Begriffe[Bearbeiten | Quelltext bearbeiten]

Signalflussgraphen sind formal definiert. Deshalb zunächst einige Begriffsdefinitionen.
- Ein Pfad ist eine zusammenhängende Folge von Verbindungen (Kanten) zwischen Knoten in einer Richtung. Im Beispiel ist (X3→X4→X5) ein Pfad.
- Ein Eingangsknoten hat nur ausgehende Pfade. X1 ist Eingangsknoten.
- Ein Ausgangsknoten hat nur eingehende Pfade. X6 ist Ausgangsknoten.
- Ein Vorwärtspfad führt in Richtung Ausgangsknoten. (X2→X3→X4) und (X3→X7→X6) sind Vorwärtspfade.
- Ein Rückwärtspfad führt in Richtung Eingangsknoten. (X5→X8→X2) ist ein Rückwärtspfad.
- Eine Rückkopplungsschleife liegt vor, wenn Anfangsknoten und Endknoten gleich sind. (X2→X3→X4→X5→X8→X2) ist eine Rückkopplungsschleife.
- Eine selbstbezogene Schleife ist ein Pfad der von einem Knoten direkt wieder zum gleichen Knoten führt, ohne über andere Knoten zu führen.
Bild 1 zeigt einen allgemeinen gerichteten, gewichteten Graphen im mathematischen Sinn. Zum Signalflussgraphen wird er erst durch folgende Vereinbarungen:
- Ein Knoten stellt ein Signal dar.
- Eine Kante stellt über ihr Gewicht die Verarbeitung des Signals dar. Sie erzeugt also ein neues Signal.
Weiterhin gilt:
- sind statische Signale.
- sind kontinuierliche Signale.
- sind deren Laplace-Transformierte.
- sind diskrete Signale.
- sind deren Z-Transformierte.
- sind Übertragungsfaktoren.
- sind kontinuierliche Impulsantwortfunktionen.
- sind kontinuierliche Übertragungsfunktionen.
- sind diskrete Impulsantwortfunktionen.
- sind diskrete Übertragungsfunktionen.
Elemente eines Signalflussgraphen[Bearbeiten | Quelltext bearbeiten]
Die Addition erfolgt im Zielknoten.

|
|
Die Multiplikation mit einer Konstanten wird unter anderem für die Verarbeitung der Koeffizienten einer Differenzialgleichung verwendet.

|
|
Die Faltung ist ein allgemeines Übertragungsglied.

|
|
Den Integrator gibt es nur in zeitlich kontinuierlichen Systemen.

|
|
Das Verzögerungsglied gibt es nur in zeitlich diskreten Systemen.

|
|
Grundschaltungen[Bearbeiten | Quelltext bearbeiten]
Für Signalflussgrafen gelten gleiche Regeln wie für Signalflusspläne. Der einzige Unterschied ist die grafische Darstellung. Auf eine Darstellung der Beziehungen im Zeitbereich wurde hier verzichtet, da diese zu unübersichtlich sind. Die Verhältnisse sind im Bildbereich wesentlich einfacher. Mit den Grundschaltungen können komplexe Signalflussgraphen umgeformt, und damit vereinfacht, werden.
Reihenschaltung

|
|
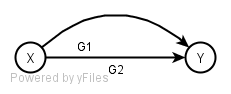
Parallelschaltung
|
|
Rückkopplung

|
|
Erstellen von Signalflussgraphen[Bearbeiten | Quelltext bearbeiten]
Aus der Differentialgleichung[Bearbeiten | Quelltext bearbeiten]
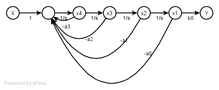
Gegeben sei die gewöhnliche, lineare, inhomogene Differenzialgleichung mit konstanten Koeffizienten 4. Ordnung
Wir führen die 4 Zustandsgrößen
ein. Damit kann die Differenzialgleichung 4. Ordnung in ein System von 4 Differenzialgleichungen 1. Ordnung
und
mit der Ausgangsgleichung
überführt werden. Wir brauchen also eine Reihenschaltung von 4 Integratoren im Vorwärtspfad des Signalflussgrafen. Die Multiplikation mit den Koeffizienten erfolgt in den zum Summations-Knoten führenden Rückwärtspfaden.
Aus der Übertragungsfunktion[Bearbeiten | Quelltext bearbeiten]

Gegeben sei die Übertragungsfunktion
- .
Nach Multiplikation von Zähler und Nenner mit hat die Übertragungsfunktion eine Form aus der sofort die benötigten Integratoren ersichtlich sind.
Im Zähler stehen die Faktoren des Vorwärtspfades und im Nenner die des Rückwärtspfades. Damit kann der Signalflussgraph direkt gezeichnet werden.
Aus dem Signalflussplan[Bearbeiten | Quelltext bearbeiten]

Durch Vertauschung von Knoten und Kanten erhält man aus dem Signalflussgraphen den Signalflussplan und umgekehrt.
Modifikationen von Signalflussgraphen[Bearbeiten | Quelltext bearbeiten]
In gleicher Weise, wie lineare Gleichungssysteme umgeformt werden können, kann auch der dazugehörige Signalflussgraph umgeformt werden. Im Folgenden werden einige Regeln erläutert.
Parallele Kanten zusammenfassen[Bearbeiten | Quelltext bearbeiten]
Unterschiedliche Kanten mit der gleichen Quelle und der gleichen Senke können zu einer Kante zusammengefasst werden. Es wird also das Distributivgesetz angewandt:
- .
Dazu müssen im Signalflussgraphen die Vektoren der zusammengefassten Kanten addiert werden[2].
 |
Sequentielle Kanten zusammenfassen[Bearbeiten | Quelltext bearbeiten]
Werden drei Punkte , und ausschließlich durch zwei Kanten derart verbunden, so dass gilt , dann kann der mittlere Knoten aus der Darstellung herausgenommen werden[2]. Es wird also das Assoziativgesetz angewandt:
- .
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Mason, Samuel J.: Feedback Theory – Some Properties of Signal Flow Graphs, Proceeding of the IRE, 1953, vol. 41, S. 1144–1156
- ↑ a b Strauß, Frieder: Grundkurs Hochfrequenztechnik, Vieweg+Teubner Verlag, Wiesbaden 2012, S. 172–175






















































