Steiner-Kette

Eine Steiner-Kette (auch Steiner’sche Kreiskette) ist in der Geometrie eine zusammenhängende Folge endlich vieler, einander berührender Kreise, deren jeder außerdem zwei vorgegebene, sich nicht schneidende Kreise – im Folgenden „Ausgangskreise“ genannt – berührt.
Die Steiner-Kette ist benannt nach dem Schweizer Mathematiker Jakob Steiner, der sie im 19. Jahrhundert definierte und viele ihrer Eigenschaften entdeckte und beschrieb.
Varianten[Bearbeiten | Quelltext bearbeiten]
Für die nachstehenden Überlegungen ist es hilfreich, sich den sukzessiven Aufbau einer Steiner-Kette vorzustellen, beginnend mit einem „Startkreis“ und endend mit einem „Endkreis“. In der üblicherweise betrachteten geschlossenen Steiner-Kette tangiert auch der Endkreis wieder den Startkreis, in einer offenen ist dies nicht der Fall. Die einzige Bedingung für die Ausgangskreise ist, dass diese einander nicht berühren oder schneiden. Das bedeutet, dass entweder ein kleinerer Kreis vollständig innerhalb eines größeren liegt oder dass die beiden Kreise, ohne einander zu berühren, außerhalb voneinander liegen.
Die Abbildung zeigt den Fall einer geschlossenen Steiner-Kette mit ineinander liegenden Ausgangskreisen – im Folgenden „Standardfall“ genannt.
Neben dem Standardfall sind etliche Varianten möglich.
Geschlossen, offen und multi-zyklisch[Bearbeiten | Quelltext bearbeiten]
Üblicherweise wird die geschlossene Steiner-Kette betrachtet, bei der der Endkreis den Startkreis wieder berührt. Ist dies nicht der Fall, bleibt eine Lücke (offene Steiner-Kette) zwischen Start- und Endkreis; wird diese geschlossen, überlappen der erste und der letzte Kreis. Wenn man eine solche Kette in weiteren „Runden“ zwischen den Ausgangskreisen fortführen kann, so dass schließlich doch ein Anschluss an das erste Glied der Kette erfolgt, spricht man von einer multi-zyklischen Kette. Die Abbildung ganz rechts zeigt eine Steiner-Kette, die nach einer ersten Runde (Übergang von den schwarz linierten Kreisen zu den grün ausgefüllten) eine zweite dreht und sich dann schließt.
- Geschlossene, offene und multi-zyklische Steiner-Kette
-
geschlossen
-
offen, überlappend
-
„multi-zyklisch“
Die Abbildungen oben zeigen der Einfachheit halber den Sonderfall einer Steiner-Kette im Kreisring.
Varianten der Kreisberührung[Bearbeiten | Quelltext bearbeiten]
Nicht nur können die beiden Ausgangskreise ineinander oder außerhalb voneinander („nebeneinander“) liegen, auch müssen die Kreise der Kette nicht zwingend alle einander extern berühren. Dies führt hinsichtlich der Berührung der beteiligten Kreise zu folgenden Varianten (die Kreise der Kette sind schwarz, die Ausgangskreise blau und rot dargestellt):
- Varianten der Kreisberührung
-
Variante 1
-
Variante 2
-
Variante 3
- Die Ausgangskreise liegen ineinander, die Kreise der Kette berühren sowohl einander als auch den inneren Ausgangskreis extern, den äußeren hingegen intern. Dies ist der Standardfall.
- Die Ausgangskreise liegen nebeneinander (blau und größer links, rot und klein etwa in der Mitte), die Kreise der Kette berühren sowohl einander als auch beide Ausgangskreise extern.
- Die Ausgangskreise liegen nebeneinander, sieben Kreise der – im Beispiel 8-gliedrigen – Kette berühren sowohl einander als auch beide Ausgangskreise extern, der achte (der schwarze ganz außen) wird von den beiden Ausgangskreisen sowie seinen beiden Nachbarn in der Kette intern berührt.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Kreiskettensatz[Bearbeiten | Quelltext bearbeiten]
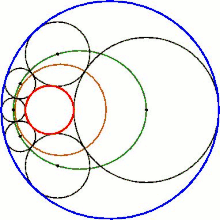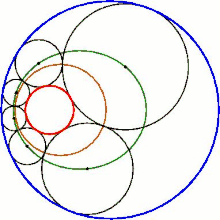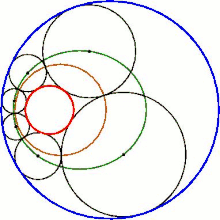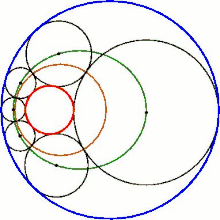
Eine fundamentale Aussage über die Steiner-Kette ist der Steinersche Kreiskettensatz (auch Schließungssatz von Steiner):[1]
- Wenn zwischen zwei Ausgangskreisen mindestens eine geschlossene Steiner-Kette möglich ist, dann sind auch unendlich viele möglich, wobei jeder beliebige Kreis, der die beiden Ausgangskreise berührt, der Startkreis einer solchen Kette sein kann.
Dies bedeutet, dass jede dieser Ketten durch Rotation der ursprünglichen Kette entlang der Ausgangskreise aus der Ursprungskette hervorgehen kann. Die Animation illustriert diesen Sachverhalt.
Mittelpunkte und Berührungspunkte[Bearbeiten | Quelltext bearbeiten]
Die Berührungspunkte der Kreise einer Steiner-Kette liegen stets auf einem Kreis (gold in der Animation).
Die Mittelpunkte der Kreise liegen auf einem Kegelschnitt. Im Standardfall (die beiden Ausgangskreise liegen ineinander) ist das eine Ellipse (grün in der Animation), deren Brennpunkte die Mittelpunkte der beiden Ausgangskreise sind. Dies ist übrigens immer dann der Fall, wenn Kreise einen vorgegebenen Kreis innen und einen weiteren vorgegebenen Kreis außen tangieren – außer bei der Steiner-Kette auch bei der Pappos-Kette, dem dreidimensionalen Soddy-Hexlet und den Apollonischen Kreisen.
Im anderen Fall (die Ausgangskreise liegen außerhalb voneinander) liegen die Mittelpunkte auf einer Hyperbel.
Generalisierungen[Bearbeiten | Quelltext bearbeiten]
- Generalisierungen
-
Pappos-Kette
-
Soddy-Hexlet
Eine Generalisierung der Steiner-Kette könnte darin bestehen, den beiden Ausgangskreisen zu erlauben, einander zu tangieren oder zu schneiden. Im ersten Fall erhält man eine Pappos-Kette mit unendlich vielen Kettengliedern.
Das Soddy-Hexlet (siehe Animation) ist eine in die dritte Dimension erweiterte, 6-gliedrige Steiner-Kette – aus den Ausgangskreisen sowie den Kreisen der Kette werden jeweils Kugeln. Die Mittelpunkte der sechs Kugeln der Kette (diese bilden das Hexlet) liegen auf derselben Ellipse wie die Mittelpunkte der Kreise der korrespondierenden Steiner-Kette. Die Einhüllende der Kugeln ist eine Dupinsche Zyklide, die Inversion eines Torus'. Die sechs Kugeln des Hexlets berühren nicht nur die innere (rot eingefärbt) und die äußere „Ausgangskugel“, sondern zusätzlich zwei weitere (in der Animation nicht dargestellte) Kugeln, die ober- bzw. unterhalb der Ebene der Hexlet-Mittelpunkte liegen.[2]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Steiner chain. In: MathWorld (englisch).
- Alexander Bogomolny: Steiner’s Chain: What is it? (interaktives Java-Applet)
- Michael Borcherds: Steiner’s Chain (interaktives Java-Applet)
- Eric W. Weisstein: Steiner’s Porism. In: MathWorld (englisch).
- Bob Allanson: Steiner’s Porism. (interaktives Java-Applet)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Thomas Bauer: Der Kreisketten-Satz von Steiner. Philipps-Universität Marburg, abgerufen am 5. April 2012.
- ↑ Bob Allanson: Soddy’s Hexlet. Abgerufen am 5. April 2012.







