Zentrierte Quadratzahl

25 Kugeln in Form ineinandergeschachtelter Quadrate

Eine zentrierte Quadratzahl ist eine Zahl, die die Summe zweier aufeinanderfolgender Quadratzahlen ist. Beispielsweise ist $13 = 4 + 9 = 2^2 + 3^2$ eine zentrierte Quadratzahl. Die ersten zentrierten Quadratzahlen sind

1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, … (Folge A001844 in OEIS)

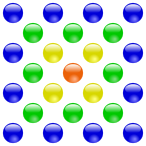
Eine zentrierte Quadratzahl beziffert eine Anzahl von Steinen, so dass ein Stein in der Mitte so von weiteren Steinen umgeben ist, dass diese ein Quadrat bilden.

1 Stein	5 Steine	13 Steine	25 Steine

Die $n$-te zentrierte Quadratzahl $ZQ_n$ berechnet sich nach der Formel

$ZQ_n = 2n^2 + 2n + 1$

Beziehungen zu anderen figurierten Zahlen

Dreieckszahlen

Die $n$-te zentrierte Quadratzahl ist eine ungerade Zahl, die um eins größer ist als das Vierfache der $n$-ten Dreieckszahl.

$ZQ_n = 1 + 4\Delta_n = 1 + 4\cdot \frac{n\cdot (n+1)}{2}$

Jede $n$-te zentrierte Quadratzahl lässt sich als Summe von Dreieckszahlen erzeugen:

$ZQ_n = \Delta_{n-1} + 2\Delta_n + \Delta_{n+1}= \frac{(n-1)n}{2} + 2\cdot \frac{n(n+1)}{2} + \frac{(n+1)(n+2)}{2}$

Quadratzahlen

Jede zentrierte Quadratzahl ist die Summe zweier aufeinanderfolgender (dezentraler) Quadratzahlen. Dies wird offensichtlich, wenn man die Berechnungsformel für die zentrierten Quadratzahlen umstellt.

$2n^2 + 2n + 1 = n^2 + (n+1)^2$

Auch an dem einer zentrierten Quadratzahl zugrundeliegenden Muster lässt sich dieser Sachverhalt erkennen:

Sonstiges

Im Vergleich zu den Quadratzahlen, die stets zusammengesetzt sind, gibt es in der Folge der Zentrierten Quadratzahlen auch einige Primzahlen. Die ersten primen zentrierten Quadratzahlen sind

5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, … (Folge A027862 in OEIS).

Abwandlungen und Verallgemeinungen

• Die dezentralen Quadrat- und Sechseckszahlen bzw. die Polygonalzahlen.
• Oktaederzahlen sind die Summen der ersten zentrierten Quadratzahlen (sh. Figurierte Zahl).

Siehe auch

• Figurierte Zahl
• Polygonalzahl und Zentrierte Polygonalzahl

Weblinks

• Eric W. Weisstein: Zentrierte Quadratzahl. In: MathWorld. (englisch)