Zirkulation (Feldtheorie)
Die Zirkulation ist das Umlaufintegral eines Vektorfeldes über einen geschlossenen Weg. Bei Strömungen ist sie ein Maß für die Wirbelstärke in dem vom Weg umschlossenen Gebiet.
Der Begriff wird in der Vektoranalysis, in der Strömungslehre und in der Elektrodynamik benutzt. Die Zirkulation kommt insbesondere im Satz von Stokes vor, der eine zentrale Rolle in der Elektrodynamik spielt.
Mathematische Formulierung[Bearbeiten | Quelltext bearbeiten]
Ist ein stückweise glatter, geschlossener und orientierter Weg im (von besonderer Bedeutung ist hier der ) und ein längs dieses Weges integrierbares Vektorfeld, so heißt
Zirkulation von längs .
Ist ein Vektorfeld auf einer orientierten und stückweise glatt berandeten Fläche differenzierbar, so ist nach dem Satz von Green die Zirkulation von längs des zu gehörigen orientierten Randes gleich dem Flächenintegral der Rotation von über :
Die komplexe Zirkulation[Bearbeiten | Quelltext bearbeiten]
Wenn das Vektorfeld in einer Ebene liegt, dann können die Eigenschaften komplexer Funktionen ausgenutzt werden. Dazu wird das Vektorfeld als komplexe Funktion aufgefasst, deren Real- und Imaginärteile die Komponenten des Vektorfeldes sind, dessen Ebene als Gauß’sche Zahlenebene modelliert wird, in der die komplexe Zahl einen Punkt markiert. Die komplexe Zirkulation ist dann das komplexe Kurvenintegral der komplexen Funktion längs einer Kurve in der Ebene. Der Realteil der komplexen Zirkulation ist die oben eingeführte reelle Zirkulation längs des Weges , also das Integral über die Komponente des Vektorfeldes, die tangential zur Kurve ist. Der Imaginärteil ist hingegen das Integral über die Komponente des Vektorfeldes, die senkrecht zur Kurve ist.
Besondere Regeln gelten, wenn die komplexe Funktion eine holomorphe Funktion ist. Wenn der Weg ein Gebiet umfasst, in dem die Funktion überall holomorph ist, dann verschwindet die komplexe Zirkulation längs des Weges identisch. Wenn eine weitere Kurve ist, die den Weg einschließt, und die Funktion im Gebiet zwischen den Kurven und holomorph ist, dann ist die Zirkulation der Funktion längs der Kurve gleich ihrer Zirkulation längs der Kurve .
Diese Aussagen werden im Folgenden begründet.
Definition[Bearbeiten | Quelltext bearbeiten]
Sei
die komplexe Funktion mit Komponenten des Vektorfeldes bezüglich eines kartesischen x-y-Koordinatensystems in der Gauß’schen Zahlenebene mit als imaginärer Einheit.
Die komplexe Zirkulation der Funktion längs des Weges ist dann das komplexe Wegintegral
Real- und Imaginärteil der komplexen Zirkulation[Bearbeiten | Quelltext bearbeiten]

Einsetzen der komplexen Funktion ergibt den Real- und den Imaginärteil:
Der Realteil
ist die oben eingeführte reelle Zirkulation längs des Weges in der Ebene. Die senkrecht zur Ebene zählenden Komponenten der hier vorkommenden Vektoren verschwinden nach Voraussetzung: Die Kurve wurde oben gemäß mit der Bogenlänge parametrisiert, so dass die Länge der Kurve ist und der Betrag des Tangentenvektors gleich eins ist, worin der Strich für die Ableitung nach der Bogenlänge steht.
Der Imaginärteil der komplexen Zirkulation ist gemäß
das Integral über die Komponenten des Vektorfeldes normal zur Kurve. Der Vektor hat den Betrag eins und steht senkrecht auf der Ebene, so dass die Normale an der Kurve ist, siehe Bild. Das Rechenzeichen bildet das Kreuzprodukt.
Wenn die Funktion eine komplexe Strömungsgeschwindigkeit ist und der Weg eine umströmte Wand darstellt, dann wird sie nicht durchflossen und die komplexe Zirkulation der komplexen Geschwindigkeit längs der Kontur ist reell.
Zirkulation holomorpher Funktionen[Bearbeiten | Quelltext bearbeiten]
Der Integralsatz von Cauchy besagt, dass das Kurvenintegral einer komplexen Funktion zwischen zwei Punkten wegunabhängig ist, wenn die Funktion holomorph also komplex differenzierbar ist. Das Kurvenintegral verschwindet demnach entlang einer geschlossenen Linie immer, wenn die Funktion in dem von der Linie umschlossenen Gebiet holomorph ist. Die Zirkulation einer Funktion entlang einer Linie kann also nur dann von null verschieden sein, wenn die Funktion irgendwo innerhalb der Linie nicht komplex differenzierbar ist.

Für die Berechnung der Zirkulation macht es keinen Unterschied, ob sie entlang eines Weges oder entlang eines anderen Weges , der den Weg umschließt, berechnet wird, sofern die Funktion im Gebiet zwischen den Wegen und holomorph ist, siehe Bild. Wenn die Funktion im gelb gezeichneten Gebiet holomorph ist, dann gilt nach dem Integralsatz von Cauchy:
Die Beiträge der Wege und gehen mit umgekehrtem Vorzeichen ein, weil bei ihnen der Integrationsweg gegenüber den Wegen und – wie im Bild angedeutet – gegensinnig durchlaufen wird. Geht die Linie in über, dann heben sich ihre beiden Beiträge auf, die Wege und werden geschlossen und es ergibt sich, dass die Zirkulation der Funktion längs des Weges gleich der längs des Weges ist:
Für den Weg kann beispielsweise – wie im Bild – ein Kreis genommen werden, wenn dieser für die Berechnung geeigneter ist.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Zirkulation des Magnetfeldes eines Stromfadens[Bearbeiten | Quelltext bearbeiten]
Ein auf der -Achse liegender Stromfaden, der in positiver -Richtung mit dem Strom durchflossen ist, wird von dem Magnetfeld
umgeben. Die Zirkulation dieses Vektorfeldes entlang eines Kreises mit und beliebigem positiven Radius ist gleich dem Strom :
Dieses Beispiel demonstriert, dass für die Anwendbarkeit des Stokes'schen Integralsatzes das betreffende Vektorfeld auf einer von der geschlossenen Kurve berandeten Fläche differenzierbar sein muss. Das Vektorfeld aus diesem Beispiel ist auf der -Achse nicht definiert. Die Zirkulation wird jedoch entlang eines Kreises gebildet, der die -Achse umschließt. Der Stokes'sche Integralsatz ist also in diesem Fall nicht anwendbar. Das bestätigt sich dadurch, dass die Zirkulation von entlang des Kreises den von null verschiedenen Wert hat, obwohl das Vektorfeld auf seinem gesamten Definitionsgebiet rotationsfrei ist ( für ).
Komplexe Zirkulation längs eines Kreises in einem Strudel[Bearbeiten | Quelltext bearbeiten]
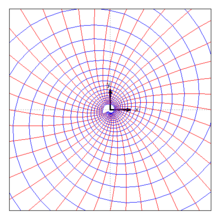
Sei
das komplexe Geschwindigkeitsfeld eines Strudels mit Zentrum bei , siehe das Bild und Potentialströmung. Die komplexe Zirkulation der Geschwindigkeit längs eines Kreises mit Radius um den Ursprung verschwindet nicht, weil die Geschwindigkeit bei nicht komplex differenzierbar ist und der Kreis diesen Punkt umschließt. Die komplexe Zirkulation der Geschwindigkeit längs des Weges
berechnet sich mit dem Differential zu
Längs des Kreises hat die Geschwindigkeit also unabhängig vom gewählten Radius immer die Zirkulation und die Quellstärke , die angibt wie groß der über den Kreis tretende Volumenstrom ist. Die komplexe Zirkulation der Geschwindigkeit längs der Kreise ist für alle Kreise gleich, weil die Geschwindigkeit im Kreisring zwischen zwei beliebigen Kreisen immer komplex differenzierbar ist.
Auch hier ist das Geschwindigkeitsfeld außerhalb des Ursprungs rotationsfrei, weil der Strudel eine Potentialströmung ist.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Königsberger: Analysis 2. Springer-Verlag Berlin, 1993. ISBN 3-540-54723-1.
- Theodore Frankel: The Geometry of Physics (An Introduction). Cambridge University Press, 1997. ISBN 0-521-38753-1.
- Michael Bestehorn: Hydrodynamik und Strukturbildung. Springer, Berlin u. a. 2006, ISBN 3-540-33796-2.














































