Dimensionsanalyse

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Die Dimensionsanalyse ist ein mathematisches Verfahren, um das Zusammenspiel physikalischer Größen bei Naturphänomenen zu erfassen, ohne die einem physikalischen Vorgang zugrundeliegende Formel oder eine exakte Gesetzmäßigkeit zu kennen. Ihre Anwendung beruht auf angewandter Mathematik, praktischer Beobachtungsgabe, der Durchführung und Auswertung von Versuchen und auf intuitivem physikalischen Verständnis. Sie hat sich insbesondere in der Strömungsmechanik bewährt.

Für wirklichkeitsnahe Probleme in Technik und Wissenschaft sind die zugeordneten mathematischen Gleichungen in den meisten Fällen aufgrund komplexer Randbedingungen nicht analytisch, sondern nur numerisch lösbar, also durch Computerverfahren. Die Anwendung der Dimensionsanalyse auf geometrisch ähnliche, jedoch labortechnisch oder numerisch leichter handhabbare Modelle erlaubt hier häufig sehr genaue Rückschlüsse auf die Lösung des hochkomplexen Ausgangsproblems.

Die Dimensionsanalyse findet hauptsächlich in der experimentellen Physik, im Ingenieurwesen, aber auch in der Medizin und Biologie Anwendung.

Teilweise wird auch die Dimensionsbetrachtung zur Prüfung der Plausibilität einer physikalischen Formel als Dimensionsanalyse bezeichnet.

Anwendungsgebiete

Die Problemstellungen und Anwendungsmöglichkeiten sind vielfältig. Einige Themenfelder sind:

• Aerodynamik und das Verhalten von Körpern in strömenden Fluiden im Allgemeinen. Etwa die Untersuchung und Optimierung der aerodynamischen Eigenschaften von Flugzeugen und Hängebrücken.
• Strömungswiderstand und Druckabbau in durchströmten Rohren.
• Bildung von Wellen und deren Ausbreitung in diversen Medien.
• Diffusion und Wärmetransport.
• Explosionsvorgänge
• Materialfestigkeitsprüfungen und Crashtests.
• Geowissenschaftlich interessant sind Auswirkungen von Erdbeben (etwa für Hochhäuser), Durchsickerungsvorgänge im Erdreich, Tragfähigkeit von Gründungen für Bauwerke oder Hangrutschungen und Lawinen.
• Im Wasserbau der Abfluss in Gerinnen und der Geschiebetransport in Flüssen.
• In Medizin und Biologie das Themengebiet der Bionik, der Blutkreislauf oder das Pflanzenwachstum.

Eine Dimensionsanalyse dieser Vorgänge liefert nützliche Proportionalitäten, Vorgaben zur Kalibrierung von Modellversuchen (s. Modellgesetze) und konkrete Anhaltspunkte für Variantenstudien. Wiederholt reicht das aus, um daraus funktionale Zusammenhänge abzuleiten. In jedem Falle trägt sie zum besseren Verständnis des Problems bei.

Historie und Überblick

Ludwig Prandtl, einer der Väter der Strömungsmechanik, und sein „handbetriebener“ Strömungskanal (1904).

Bereits Physiker wie Ludwig Prandtl, Theodore von Kármán, Albert Shields, Johann Nikuradse und John William Strutt, 3. Baron Rayleigh, die sich Ende des 19. und zu Beginn des 20. Jahrhunderts als erste tiefergehend mit den Eigenschaften von Strömungen und bewegten Körpern in Fluiden beschäftigten, nutzten die Dimensionsanalyse, um vom Laborexperiment mit kontrollierbaren Randbedingungen auf das Verhalten physikalischer Probleme mit geometrisch ähnlichen Körpern oder mit Fluiden anderer Zähigkeit und Dichte zu schließen. Dieses Ähnlichkeitsprinzip, also die Möglichkeit, physikalische Phänomene in unterschiedlichen Maßstäben untersuchen zu können, bildet die Grundlage der Ähnlichkeitstheorie. Häufig wird diese Theorie auch als Modelltheorie bezeichnet.

Die der Ähnlichkeitstheorie zugrundeliegende Dimensionsanalyse besagt, dass sich jede dimensionsgebundene physikalische Formel $y=f(x_{1},x_{2},\dots ,x_{n})$ in eine dimensionslose, d. h. von physikalischen Einheiten bereinigte Gestalt überführen lässt. Dazu werden $y$ und $f(x_{1},x_{2},\dots ,x_{n})$ durch ein Potenzprodukt der Variablen $x_{1},x_{2},\dots$ geteilt und gleichzeitig die einzelnen $x_{i}$ in beliebige Potenzen erhöht:

${\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}={\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}},\,k_{i}\in \mathbb {R} \neq 0,$

so dass die linke und die rechte Seite der Gleichung dimensionslos werden. Die Dimensionsreinheit und damit die Korrektheit jeder physikalischen Beziehung lässt sich anhand dieser Aussage prüfen. Genügt eine Formel nicht diesen Kriterien, dann ist sie physikalisch nicht exakt. Dies gilt für viele Näherungsformeln, die bewusst bestimmte Größen vernachlässigen. Auch ist klar, dass nur Größen gleicher Dimension addiert und subtrahiert werden können, also untereinander vergleichbar sind. Die Argumente etwa trigonometrischer oder anderer transzendenter Funktionen müssen folglich dimensionslose Zahlen sein.

Das wichtige, auf der Dimensionsanalyse aufbauende, und unabhängig voneinander von Aimé Vaschy (1890), Dmitri Pawlowitsch Rjabuschinski (1911) und Edgar Buckingham (1915) bewiesene Π-Theorem, erweitert obige Aussage dahingehend, dass sich die Funktion $y=f(x_{1},x_{2},\dots ,x_{n})$ in der allgemeineren Form

${\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p}),\,k_{i}\in \mathbb {R} \neq 0$

darstellen lässt. Die Potenzprodukte der $x_{n}$, die so genannten $\Pi$-Faktoren in $G$ mit $p<n$, sind dimensionslos.

Durch die Dimensionsanalyse ist es möglich, die funktionale Gestalt physikalischer Formeln bis auf eine reellwertige Konstante $C$ zu „erraten“, sofern nur wenige physikalische Größen Einfluss nehmen, wie beispielsweise beim erstmals von Galilei formulierten Fallgesetz

$s(t)=C\cdot g\cdot t^{2}$

mit $s$ als dem Fallweg, $g$ als der Fallbeschleunigung und $t$ als der Zeit. Die Proportionalitätskonstante $C$ verbleibt dabei im Experiment zu bestimmen; sie ergibt sich zu $C=0{,}5$.

Dimensionen und Maßsysteme

Basisgrößen und deren Einheiten in der Physik

Die Begriffe von Zeit…

… oder Länge, hier veranschaulicht durch das Urmeter, erfassen eigenständige Dimensionen.

Messen einer physikalischen Größe heißt Größenarten (z. B. Geschwindigkeit, Druck) mit etwas vergleichen.

Für solche Vergleiche benötigt man nie mehr als sieben Grundgrößenarten, die man Basisgrößenarten nennt. Für sie sind über Prototypen Basiseinheiten (z. B. Meter, Sekunde) definiert. Jede Basisgrößenart stellt eine eigene Dimension dar, die nicht über die restlichen Basisgrößenarten beschrieben werden kann. Sie sind alle voneinander unabhängig.

→ Hauptartikel: „SI-Basiseinheiten“ im Artikel Internationales Einheitensystem

Grundgrößensysteme

Ein Grundgrößensystem beinhaltet alle Dimensionen, in denen ein Messvorgang stattfindet. Ein System, das alle bekannten Dimensionen – L = Länge, M = Masse, T = Zeit, I = Stromstärke, Θ = thermodynamische Temperatur, N = Stoffmenge und J = Lichtstärke – enthält, heißt {L,M,T,I,Θ,N,J}-System. Es ist ausreichend, um alle Vorgänge in der Natur zu erfassen. In der Mechanik, dem Hauptanwendungsgebiet der Dimensionsanalyse, kann man sich meist auf ein {L,M,T}-System beschränken.

Im Grundgrößensystem selbst ist die explizite Wahl einer Basiseinheit belanglos. Die Länge [L] wird so etwa mit den Basiseinheiten Meter, Fuß, Zentimeter, Yard etc. gemessen. Die Basiseinheit dient aber nur einem Vergleichszweck, sie ist nicht mit der Dimension zu verwechseln.

Grundgrößensysteme können nicht nur aus denjenigen Grundgrößenarten gebildet werden, die auch gleichzeitig Basisgrößenarten sind, sondern auch mit allen anderen. So ist nach Newton die Kraft als zusammengesetzte Größe aus Masse und den Grundgrößenarten Länge und Zeit geeignet, die Masse in einem {L,M,T}-System zu ersetzen. Dann entsteht ein {L,F,T}-System mit der Grundgrößenart Kraft [F] an Stelle der Masse, über die sie definiert ist. Die Kraft besitzt hier als Dimensionsbegriff eine eigene, unabhängige Dimension, welche den Massenbegriff einschließt.

Äquivalenz von Grundgrößensystemen

Alle Größenarten eines {M,L,T}-System lassen sich auch in einem {F,L,T}-System angeben. Ein {M,F,L,T}-System darf es wegen der Abhängigkeit von Masse und Kraft nicht geben. Die Forderung nach voneinander unabhängigen Dimensionen wäre verletzt.

Man kann alternativ Grundgrößensysteme wählen, in denen der Druck, die Geschwindigkeit oder die Frequenz Grundgrößen sind. Bedingung ist, dass jede Grundgröße für sich eine von den anderen verwendeten Grundgrößen unabhängige Dimension darstellt.

Man nennt alle Grundgrößensysteme, in denen dieselben Größen dargestellt werden können, äquivalent. Für das Auffinden von so genannten Π-Faktoren ist die explizite Wahl von Grundgrößen belanglos. Sie ist nur eine Frage der bevorzugten Darstellungsweise.

In der Mechanik gebräuchliche Größenarten in einem {M,L,T}-System sind nachfolgend mit ihren Dimensionsformeln aufgelistet. Ihre Einheiten sind Potenzprodukte der Basiseinheiten. Ihre Dimensionsformeln sind Potenzprodukte der Dimensionen, innerhalb derer diese Einheiten beschrieben sind.

In der Mechanik gebräuchliche Größenarten in einem {M,L,T}-System

Größenart	Größenbezeichnung (Formelzeichen)	Einheit	Dimensionsformel
Masse	$m$	kg	$M$
Länge	$l$, $b$, $h$, …	m	$L$
Zeit	$t$	s	$T$
Frequenz	$f$	Hz (= 1/s)	$T^{-1}$
Winkelgeschwindigkeit	$\omega$	1/s	$T^{-1}$
Geschwindigkeit	$v$	m/s	$L\cdot T^{-1}$
Beschleunigung	$a$	m/s²	$L\cdot T^{-2}$
Impuls	$p$	m·kg/s	$M\cdot L\cdot T^{-1}$
Dichte	$\rho$	kg/m³	$M\cdot L^{-3}$
Kraft	$F$	N (= kg·m/s²)	$M\cdot L\cdot T^{-2}$
Wichte	$\gamma$	N/m³	$M\cdot L^{-2}\cdot T^{-2}$
Druck, Spannung	$p$	N/m²	$M\cdot L^{-1}\cdot T^{-2}$
Elastizitätsmodul	$E$	N/m²	$M\cdot L^{-1}\cdot T^{-2}$
Energie	$W$	J (= m²·kg/s²)	$M\cdot L^{2}\cdot T^{-2}$
Leistung	$P$	W (= m²·kg/s³)	$M\cdot L^{2}\cdot T^{-3}$
Dynamische Viskosität	$\mu$	N·s/m²	$M\cdot L^{-1}\cdot T^{-1}$
Kinematische Viskosität	$\nu$	m²/s	$L^{2}\cdot T^{-1}$

Formulierungen, wie „maßgebliche Größe der Dichte“ oder „Einfluss der Größen Geschwindigkeit und Beschleunigung“, sind umgangssprachlich. Diese Verwendung des Begriffs Größe ist im physikalischen Sinne nicht korrekt. Dichte, Geschwindigkeit, Beschleunigung usw. sind Größenarten. Erst in einer Gleichung der Art:

$v=3\,\mathrm {m/s}$

wird eine Größe $v$ (man kann auch von Messgröße sprechen) über eine (Maß-)Einheit [m/s] und eine Maßzahl 3 beschrieben. Für technische Zwecke ist dies aber nicht relevant.

Grundgrößensysteme und ihre Transformationen

Jedes Grundgrößensystem kann mithilfe einer Übergangsmatrix, welche die Exponenten der Dimensionen enthält, in ein dazu äquivalentes überführt werden. Möchte man in einem Grundgrößensystem beispielsweise die Dimension der Kraft $F$, gegeben in der Form

$F^{1}=M^{1}\cdot L^{1}\cdot T^{-2}$,

durch die Masse $M$ ausdrücken, so gelingt dies durch die einfache algebraische Umstellung

$M^{1}=F^{1}\cdot L^{-1}\cdot T^{2}$.

Oder, in übersichtlicher Form dargestellt, mit der Übergangsmatrix der Exponenten $D_{1}$

$D_{1}={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\\mathbf {M} &1&-1&2\\\mathbf {L} &0&1&0\\\mathbf {T} &0&0&1\\\end{pmatrix}}$

Die Transformation der Grundgrößen des {M,L,T}-Systems zum {F,L,T}-Grundgrößensystem ist durch die Matrizenmultiplikation

$R\cdot D_{1}={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\m&1&0&0\\l,b,h,\dots &0&1&0\\t&0&0&1\\f&0&0&-1\\\omega &0&0&-1\\v&0&1&-1\\a&0&1&-2\\\rho &1&-3&0\\F&1&1&-2\\\gamma &1&-2&-2\\p,E&1&-1&-2\\W&1&2&-2\\P&1&2&-3\\\mu &1&-1&-1\\\nu &0&2&-1\\\end{pmatrix}}\cdot {\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\\mathbf {M} &1&-1&2\\\mathbf {L} &0&1&0\\\mathbf {T} &0&0&1\\\end{pmatrix}}={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\m&1&-1&2\\l,b,h,\dots &0&1&0\\t&0&0&1\\f&0&0&-1\\\omega &0&0&-1\\v&0&1&-1\\a&0&1&-2\\\rho &1&-4&2\\F&1&0&0\\\gamma &1&-3&0\\p,E&1&-2&0\\W&1&1&0\\P&1&1&-1\\\mu &1&-2&1\\\nu &0&2&-1\\\end{pmatrix}}=Q$.

möglich, wenn die Dimensionsmatrix $R$ die Exponenten aller Dimensionsformeln des {M,L,T}-Systems enthält. Die gesuchten Exponenten der Dimensionsformeln im {F,L,T}-System finden sich dann in der Dimensionsmatrix $Q$.

Da Länge und Zeit durch die Transformation unberührt bleiben, ändern sich lediglich die Exponenten derjenigen Größen, die mit der Dimension der Masse $M$ korreliert sind. Man erkennt, dass sich für einige Grundgrößen, wie beispielsweise den Druck $p$, die Dimensionsformeln vereinfachen. Für andere hingegen, wie die direkt von der Masse abhängende Dichte $\rho$, jedoch verkomplizieren. Es ist nützlich ein solches Grundgrößensystem zu bilden, in dem sich die Größen des konkreten Problems möglichst einfach darstellen lassen.

Π-Faktoren

Definition

$\Pi$-Faktoren nennt man diejenigen Produkte, die sich aus einer Matrix wie der obigen Dimensionsmatrix $R$ ergeben, wenn man einzelne Größen in beliebige Potenzen erhebt und sie mit anderen in der Matrix vorkommenden Größen derart multipliziert, dass das Produkt dimensionslos wird bzw. die Dimension 1 besitzt. Die Dimension einer Größe $x$ wird durch das Klammerzeichen $[x]$ angegeben. Beispielsweise ist das Potenzprodukt

$\Pi =v^{1}\cdot a^{-1}\cdot t^{-1}$

ein $\Pi$-Faktor der Matrix $R$, der die geforderte Dimension

$[\Pi ]=L^{1}\cdot T^{-1}\cdot L^{-1}\cdot T^{2}\cdot T^{-1}=1$

besitzt. Die Dimension 1 bleibt natürlich auch dann erhalten, wenn man $\Pi$ in beliebige Potenzen erhebt. Es ist:

$[\Pi ^{2}]=[{\sqrt {\Pi }}]=[\Pi ^{\lambda }]=1,\,\lambda \in \mathbb {R} \neq 0$

Anzahl der Π-Faktoren

Es sind beliebig viele Darstellungen eines einmal gefundenen Faktors möglich. Die Anzahl der $\Pi$-Faktoren, die nicht als Potenz eines vorher gefundenen Faktors oder als Produkt von in Potenzen erhobenen Faktoren geschrieben werden können, ist allerdings beschränkt. Über die Existenz dieser $\Pi$-Faktoren in einer gewählten Dimensionsmatrix $A$ kann gesagt werden, dass es genau $p=n-r$ linear unabhängige $\Pi$-Faktoren gibt.

Dabei sind:

• p: Die Anzahl der dimensionslosen $\Pi$-Faktoren
• n: Die Anzahl der dimensionsgebundenen Größen
• r: Der Rang der Matrix $A$.

Formale Vorgehensweise für eine Dimensionsanalyse

$A$ ist als Dimensionsmatrix mit $n$ Zeilen für die Größen $x_{n}$ und 3 Spalten für 3 Dimensionen $Y_{j}$ zu wählen:

$(1)\quad A={\begin{pmatrix}&Y_{1}&Y_{2}&Y_{3}\\x_{1}&a_{11}&a_{12}&a_{13}\\x_{2}&a_{21}&\ddots &\ddots \\x_{3}&a_{31}&\ddots &\ddots \\\vdots &\ddots &\ddots &\vdots \\x_{n}&a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}$

Findet man einen Zeilenvektor $k$ mit der Spaltenanzahl $n$, für den gilt:

$(2)\quad k\cdot A={\begin{pmatrix}k_{1}&k_{2}&k_{3}&\dots &k_{n}\end{pmatrix}}\cdot {\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&\ddots &\vdots \\a_{31}&\ddots &\vdots \\\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}={\begin{pmatrix}0&0&0\\\end{pmatrix}}$

dann hat man mit:

$(3)\quad \Pi =x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}$

einen $\Pi$-Faktor von $A$ gefunden.

Kontrollmöglichkeiten

Die Anzahl linear unabhängiger Zeilenvektoren, die diese Gleichung (2) erfüllen, ist $p$. Ihre lineare Unabhängigkeit beweist man, indem man zeigt, dass der Rang der Matrix $K$, die man aus $p$ gefundenen Zeilenvektoren bilden kann, ebenfalls $p$ ist.

$(4)\quad \mathrm {rg} (K)={\begin{pmatrix}k_{11}&k_{12}&k_{13}&\dots &k_{1n}\\\vdots &\vdots &\vdots &\vdots &\vdots \\k_{p1}&k_{p2}&k_{p3}&\dots &k_{pn}\\\end{pmatrix}}=p$

Multipliziert $K$ mit $A$ ergibt sich die Nullmatrix $0$ mit der Anzahl der gewählten Dimensionen (hier: 3) als Spalten und der Anzahl der Vektoren als Zeilen.

$(5)\quad {\begin{pmatrix}k_{11}&k_{12}&k_{13}&\dots &k_{1n}\\\vdots &\vdots &\vdots &\vdots &\vdots \\k_{p1}&k_{p2}&k_{p3}&\dots &k_{pn}\\\end{pmatrix}}\cdot {\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&\ddots &\vdots \\a_{31}&\ddots &\vdots \\\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}={\begin{pmatrix}0&0&0\\\vdots &\vdots &\vdots \\0&0&0\\\end{pmatrix}}$

Aus der Matrixalgebra ergibt sich, dass auch jede beliebige Linearkombination der gefundenen Zeilenvektoren Gleichung (2) löst, und damit einen $\Pi$-Faktor darstellt. Demnach ist (5) auch für jede Matrix erfüllt, die sich aus $K$ ergibt, indem man Zeilen mit beliebigen reellen Zahlen verschieden von Null multipliziert und mit anderen Zeilen addiert oder subtrahiert. Am Rang der Matrix $K$ ändert sich nichts. Für die Anzahl möglicher Lösungsmöglichkeiten heißt dies, dass man mit $p$ gefundenen $\Pi$-Faktoren beliebig viele andere $\Pi$-Faktoren bilden kann:

$(6)\quad \Pi =\Pi _{1}^{\lambda _{1}}\cdot \Pi _{2}^{\lambda _{2}}\cdot \quad \cdot \Pi _{p}^{\lambda _{p}},\,\lambda _{i}\in \mathbb {R} \neq 0,$

wobei deren zugehörige Zeilenvektoren homogene Lösungen von (2) wären. Es sind allerdings weiterhin nur genau $p$ $\Pi$-Faktoren, die ein Fundamentalsystem der Dimensionsmatrix bilden.

Schlussfolgerungen

• Mit einem beliebigen Fundamentalsystem sind über (6) alle existierenden Lösungen von (2) bestimmt. Dabei sind beliebig viele Lösungen darstellbar.
• Dimensionslose Zahlenkonstanten, die oft schon Verhältnisgrößen sind, bleiben bei dieser Rechnung dimensionslos und stellen automatisch einen dimensionslosen Π-Faktor dar.

Auffinden eines Fundamentalsystems von Π-Faktoren

Analytisches Vorgehen

Eine erste Möglichkeit ein Fundamentalsystem von $\Pi$-Faktoren zu erlangen besteht darin, die unabhängigen Variablen $k_{i}$ im Gleichungssystem, das sich aus (2) ergibt, beliebige Werte außer Null annehmen zu lassen und den Rang der Zeilenmatrix nach (4) zu prüfen. Die Anzahl der unabhängigen Variablen ist identisch mit der Anzahl der $\Pi$-Faktoren.

Unabhängig oder frei wählbar sind im Gleichungssystem diejenigen Variablen, denen man beliebige Zahlenwerte zuweisen kann, ohne in der Lösung einen Widerspruch herbeizuführen. Eine geschickte Wahl ist es beispielsweise, immer einer unabhängigen Variablen den Zahlenwert Eins zuzuweisen und die anderen unabhängigen Variablen auf Null zu setzen. Die fehlenden abhängigen Variablen ergeben sich durch die Lösung des verbleibenden Gleichungssystems.

Der Nachteil dieser Methode besteht jedoch darin, dass man recht wenig Einfluss auf das Aussehen dieses Fundamentalsystems hat und unter Umständen eine Vielzahl von Gleichungssystemen lösen muss.

Methode des Erratens

Eine zweckmäßigere Methode ist es, einzelne $\Pi$-Faktoren schlichtweg aus (1) zu erraten. Dazu muss man die Zeilen der Größen in der Dimensionsmatrix $A$ „zu Null“ addieren.

Praktisch heißt dies:

• Will man eine Größe im Zähler, muss man ihre Zeile mit „+1“ multiplizieren, andernfalls mit „−1“. (Die Zeilen mit Zahlen zu multiplizieren bedeutet die Größen in die entsprechenden Potenzen zu erheben.)
• Ergibt die Addition solcher Zeilen Null, besitzt man ein Potenzprodukt (wie zuvor mit der Matrix $S$ demonstriert).

Diese Methode beinhaltet die Möglichkeit, das Aussehen von $\Pi$-Faktoren zu beeinflussen. Allerdings muss man im Nachhinein den Rang der resultierenden Zeilenmatrix bestätigen, beispielsweise indem man eine nichtverschwindende Unterdeterminante findet, also zeigt, dass (4) erfüllt ist.

Wertung der Methoden

Meist führt das Erraten der Faktoren bei geschickter Wahl des Grundgrößensystems und übersichtlichen Verhältnissen wesentlich schneller zum Ziel als ein formales Vorgehen.

In der Literatur zur linearen Algebra werden noch weitere Methoden zum analytischen Auffinden der $\Pi$-Faktoren demonstriert, um das Gleichungssystem aus (2) möglichst geschickt zu lösen, z. B. das gaußsche Eliminationsverfahren.

Bildung physikalisch nützlicher Fundamentalsysteme

Ist man zu einem Fundamentalsystem gelangt, befriedigt dies oftmals nicht den Wunsch nach einer physikalischen Aussagekraft der einzelnen $\Pi$-Faktoren. Abhilfe schafft die Anwendung von Gleichung (6).

Durch geschicktes Kombinieren der Faktoren untereinander und ihre Erhebung in beliebige Potenzen kann leicht ein neuer, physikalisch ergiebigerer Faktor gebildet werden. Soll dieser in einem neuen Fundamentalsystem vorhanden sein, ist lediglich einer der Faktoren zu streichen, durch deren Kombination man den neuen gebildet hatte. Dadurch wird der neu erlangte $\Pi$-Faktor linear unabhängig von den restlichen. Angenommen, dass es ein Fundamentalsystem mit $\Pi _{1},\Pi _{2},\Pi _{3}$ als $\Pi$-Faktoren gibt, und ein neuer, aussagekräftigerer Faktor die Gestalt

$\Pi _{4}=\Pi _{1}^{-1}\cdot \Pi _{2}^{2}$

hätte, dann wäre ein neues Fundamentalsystem $\Pi _{1},\Pi _{3},\Pi _{4}$ oder $\Pi _{2},\Pi _{3},\Pi _{4}$ , jedoch nicht $\Pi _{1},\Pi _{2},\Pi _{4}$ , da ja $\Pi _{4}$ von den ersten beiden linear abhängt.

Für Modelluntersuchungen ist es nützlich, solche Faktoren gebildet zu haben, die immer eine charakteristische Größe enthalten, die dann nur in einem einzigen Faktor vorkommt. Dies muss nicht unbedingt möglich sein. Gleichung (6) erlaubt aber das zu prüfen.

Dimensionshomogene Funktionen

Wenn es eine dimensionshomogene Funktion mit einem dimensionsgebundenen Funktionswert $y$ gibt, der über Größen $x_{i}$ bestimmt ist, also

$(7)\quad y=f(x_{1},x_{2},\dots ,x_{n});\,\,[y]=[f(x_{1},x_{2},\dots ,x_{n})]\neq 1$

dann findet sich immer ein Potenzprodukt derart, dass sich schreiben lässt:

$(8)\quad {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}={\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}},\,k_{i}\in \mathbb {R} \neq 0$

$\left[{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right]=\left[{\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right]=1$

Jede physikalische Formel und insbesondere ihr an eine Einheit gebundener Funktionswert $y$ lassen sich also über Potenzerhebung der in der Funktion $f$ enthaltenen Größen $x_{i}$ dimensionslos darstellen.

Aussagen des Π-Theorems

Das so genannte $\Pi$-Theorem (in der Literatur auch oft Buckingham-Theorem), leitet einen Schritt weiter. Seine Hauptaussage ist, dass sich jede dimensionsgebundene Gleichung

$y=f(x_{1},x_{2},\dots ,x_{n});\quad [y]=[f(x_{1},x_{2},\dots ,x_{n})]\neq 1$

in die Form von

$(9)\quad {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})$

$\left[{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}\right]=\left[G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})\right]=1,\,k_{i}\in \mathbb {R} \neq 0,\,p\,{\text{wie vorher}}$

überführen lässt und damit nur aus dimensionslosen Potenzprodukten (und Zahlenkonstanten) aufgebaut ist. Dabei kann es sein, dass es mehrere Möglichkeiten gibt, die linke Seite der Gleichung in dimensionsloser Form darzustellen. Gelegentlich wird in der Literatur die linke Seite ebenfalls als Π-Faktor bezeichnet. Dies ist legitim, aber nicht konsequent, denn durch die Trennung in linke und rechte Seite erhält man die präzisere Aussage

${\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}-G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})=0$

an Stelle von

$F\left(\Pi _{1},\Pi _{2},\dots ,\Pi _{p},{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right)=0$

Die Bedeutung des Theorems liegt darin, dass eine Aussage über den funktionalen Zusammenhang dimensionsbehafteter physikalischer Größen gemacht werden kann, der sich vielleicht nicht explizit formelmäßig angeben lässt. Dies gilt für viele komplexe Sachverhalte in der Natur (z. B. Turbulenz, Kármánsche Wirbelstraße). Da Größen nur noch in bestimmten Relationen, den vorgestellten Π-Faktoren, zueinander auftreten können, erreicht man gleichzeitig eine nützliche Reduktion der Funktionsvariablen in $G$ gegenüber denen in $f$, denn es gilt wiederum $p=n-r$.

Schlussfolgerungen

Ist die Anzahl $p$ der Π-Faktoren klar, dann gilt:

• Bei $p=0$ ist der gesuchte funktionale Zusammenhang bis auf eine Proportionalitätskonstante bestimmt.
• Existieren einer oder mehrere Faktoren ($p>0$), dann kann ein funktionaler Zusammenhang, etwa aus experimentellen Ergebnissen oder durch pure Intuition, nur erraten werden. Explizit herleiten lässt er sich nicht.

Häufig trifft im zweiten Fall der Produktansatz nach Rayleigh zu, also dass die gefundenen Π-Faktoren miteinander multipliziert und in eine entsprechende, oft ganzzahlige Potenz erhöht, das gesuchte Endergebnis liefern.

Es lassen sich noch zwei allgemeinere Schlussfolgerungen ziehen:

• Satz 1: Wenn eine Größe $x_{a}$ nicht dazu benötigt wird, auf ein Fundamentalsystem von Π-Faktoren zu gelangen oder $y$ dimensionslos zu machen, dann hängt $y$ entweder nicht von $x_{a}$ ab, oder der gedachte funktionale Zusammenhang muss um mindestens eine weitere Größe erweitert werden.
• Satz 2: Wenn $y$ durch kein Potenzprodukt aus den $x_{i}$ dimensionslos gemacht werden kann, dann ist die Dimensionsmatrix unvollständig oder falsch.

Das bedeutet, dass man in jedem Falle bei dimensionsbehafteten Gleichungen, was physikalische Formeln immer sind, zu einer vorteilhaften, dimensionslosen Darstellung gelangen kann, in der die Einheiten der Größen keine Rolle spielen.

Diese fundamentalen Prinzipien sind bedeutsam für die gesamte Physik.

Vektoren und Tensoren

An ihre Grenzen stößt die Dimensionsanalyse, wenn nicht nur skalare Größen wie Druck oder Temperatur oder eindimensionale, gerade Bewegungsvorgänge behandelt werden, sondern Vektoren und Tensoren ins Spiel kommen.

Da nur eine physikalische Dimension der Länge zur Verfügung steht, für die Beschreibung von räumlichen Vorgängen aber ein dreidimensionales kartesisches Koordinatensystem nötig ist (wobei Vektoren ins Spiel kommen), müsste für den zweidimensionalen Parabelflug einer Kanonenkugel etwa deren zeitabhängige Höhe und Weite getrennt untersucht werden. Dies schließt nicht aus, dass man über die Kenntnis von Symmetrien in beiden Formeln und dem nötigen Hintergrundwissen die eine gültige Bestimmungsgleichung für den Flug innerhalb eines rechtwinkligen und unbewegten Koordinatensystems herleiten kann. Wird die Kugel zusätzlich noch durch Seitenwind abgelenkt, und das Problem damit dreidimensional, steigt die zu erfassende Komplexität weiter.

Der scheinbare Widerspruch zwischen den drei Dimensionen des Raumes und der einen zur Verfügung stehenden Dimension der Länge löst sich auf, wenn man diese Längendimension gedanklich in einem mitwandernden Koordinatensystem an der Flugkurve selbst ausrichtet. Folgt man der Bahn, ist die Kurve und die Kugelgeschwindigkeit eindimensional. Die Dimensionsanalyse ist also durchaus gültig. Die Bahngeschwindigkeit entlang der Kurve lässt sich eindimensional, nämlich über den Betrag des Geschwindigkeitsvektors, erfassen. Dies ist nur für einen unbewegten Beobachter wenig hilfreich, der nicht nur Kenntnis über Beträge der Geschwindigkeit oder den zurückgelegten Weg der Kugel, sondern auch über die Richtung der Geschwindigkeit und die Kugelposition im Raum erlangen möchte.

Ähnliches gilt etwa für dreidimensionale Spannungszustände (etwa bei Untersuchung von Materialfestigkeiten), die mit einem Spannungstensor erfasst werden müssten.

Übergang zur Modelltheorie

Die dritte wichtige Schlussfolgerung, die das $\Pi$-Theorem in der experimentellen Versuchstechnik bedeutsam macht, ist diejenige:

Ähnlichkeit von Luftwirbeln im Kleinen …

… und im Großen beim Hurrikan Fran.

• Satz 3: Wenn in der dimensionslosen Funktionsgleichung

${\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p}),\,k_{i}\in \mathbb {R} \neq 0$ alle $\Pi$-Faktoren auf der rechten Seite der Gleichung konstant gehalten werden, dann wird auch das dimensionslose Funktionsergebnis auf der linken Seite immer dasselbe sein.

Satz 3 ist entscheidend für die gesamte Ähnlichkeitstheorie. Alle Randbedingungen, die in realistischen Modellversuchen zu wählen sind, gehen hieraus hervor (s. vollständige und teilweise Modellähnlichkeit).

Als Beispiel für einen in Modellversuchen bedeutenden Π-Faktor sei die Reynolds-Zahl genannt. Diese ist:

$Re={\frac {\rho \cdot v\cdot L}{\mu }}={\frac {v\cdot L}{\nu }}$ mit: $\mu =\nu \cdot \rho$

Da in die Reynolds-Zahl eine geometrische Länge $L$, die Strömungsgeschwindigkeit $v$ die Dichte $\rho$ und die Viskosität $\mu$ eingehen, ist es möglich, maßstabsgetreue kleinere Modelle (etwa Flugzeuge im Strömungskanal) zu untersuchen, und dennoch ein korrektes Ergebnis auf der linken Seite der obigen dimensionslosen Funktionsgleichung zu erhalten, indem man bei der Untersuchung des Modells $v$ und/oder $\nu$ anpasst.

Bei vielen Problemstellungen tauchen dieselben charakteristischen Π-Faktoren wiederkehrend auf. So sind viele, unter dem Stichwort dimensionslose Kennzahl, nach ihren Entdeckern und Erforschern benannt.

Vollständige und teilweise Modellähnlichkeit

Wenn es gelingt, alle Π-Faktoren in einem physikalisch interessierenden Wertebereich konstant zu halten, spricht man von vollständiger Modellähnlichkeit, ansonsten von teilweiser Modellähnlichkeit.

Oftmals glückt die vollständige Modellähnlichkeit allerdings nicht, und man ist gezwungen, den mehr oder weniger großen Nebeneffekt auf das letztendliche Messergebnis abzuschätzen. Nebeneffekte können auch anderweitig auftreten, nämlich wenn eine Größe, deren Einfluss auf den Prototyp belanglos wäre, das Modell unerwünscht stark beeinflusst (s. Froude-Zahl im Schiffsmodell).

Kavitation bei einem Propeller im maßstäblichen Modellversuch. Die Konstanz von Reynoldszahlen in Modell und Prototyp verlangt die vierfache Umdrehungs­geschwindigkeit des Modellpropellers, wenn sein Durchmesser halbiert wird.

Modellgesetze

Über die Gleichsetzung der Π-Faktoren von Modell und Prototyp ergeben sich Modellgesetze. Variiert man in der Reynoldszahl des Modells gegenüber dem Prototyp die Länge, kann man dies, wie oben erklärt, durch Anpassung der Viskosität und/oder der Geschwindigkeit ausgleichen.

Um die Modellgesetze in eine vorteilhafte Form zu bringen, ist man immer bestrebt, nur diejenigen Größen in die Π-Faktoren zu übernehmen, die man auch im Modell variieren kann und nicht diejenigen, die sich aus der Konsequenz dieser Variation ergeben würden. Die praktisch sinnvollste Form erreicht man, wenn es möglich ist, diese Gleichungen derart zu schreiben, dass beim Einsetzen der Größenwerte des Prototyps immer eine eindeutige Aussage über eine einzelne Versuchseinstellung im Modell möglich ist. Also dergestalt, dass sich bei jeder Änderung der Ausgangssituation im Prototyp immer die erforderliche Versuchseinstellung im Modell offenbart.

Modellversuche

Ein nicht zu unterschätzender Vorteil liegt überdies noch darin, in einem Modellversuch nicht mehr alle einfließenden Größen einzeln variieren zu müssen, sondern nur noch die aus ihnen gebildeten, und von der Anzahl her geringeren, Π-Faktoren. Auch für die Darstellung der späteren Versuchsergebnisse ist dies von entscheidender Bedeutung. Indem man nur noch Π-Faktoren statt einzelner, dimensionsbehafteter, Größen aufträgt, gelangt man zu einer wesentlich knapperen und übersichtlicheren Veranschaulichung der Messgrößen (man spart Dimensionen). Alle Diagramme, in denen die Achsen dimensionslos dargestellt sind, basieren auf der Grundlage der Dimensionsanalyse.

Beim Bau eines Modells und der späteren Versuchsdurchführung muss man sorgfältig alle relevanten Größen im Voraus überlegen. Nur über die richtigen Parameter gelangt man auf die richtigen oder einen vollständigen Satz von Π-Faktoren und kann eine realistische Simulation durchführen. Bei Auswahl zu vieler Größen, die möglicherweise nur geringe Bedeutung auf die Messung haben, steigt jedoch die Anzahl der Versuche gewaltig. Dies erfordert physikalischen Sachverstand.

Vielleicht stellt sich im Nachhinein heraus, dass eine Größe, der man eine Bedeutung zugedacht hatte, wesentlich weniger Einfluss auf das Ergebnis hat als angenommen. Falls diese Größe nur in einem einzigen Faktor vorkommt, ist es möglich, diesen zu streichen. Ansonsten empfiehlt es sich, mit einem neuen Satz von Größen die Dimensionsmatrix zu bilden und ein passendes Fundamentalsystem zu finden.

Beispiele

Um die Anwendung der Formeln aus den vorhergehenden Kapiteln zu demonstrieren, folgen einige Rechenbeispiele.

Galileis Fallgesetz

Zunächst sei fälschlicherweise angenommen, dass im Fallgesetz von Galileo Galilei der Fallweg $s$ neben der Fallbeschleunigung $g$ und Zeit $t$ auch von der Masse $m$ des fallenden Körpers abhinge, also:

$s=f(g,t,m)\,$

Die zugeordnete Dimensionsmatrix $A$ lautet in ausführlicher Schreibweise

$A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\g&0&1&-2\\t&0&0&1\\m&1&0&0\\\end{pmatrix}}$

bzw. in mathematisch exakter Formulierung

$A={\begin{pmatrix}0&1&-2\\0&0&1\\1&0&0\end{pmatrix}}.$

Da alle Zeilenvektoren von $A$ linear unabhängig sind, ergibt sich der Rang zu $\mathrm {rg} (A)=3$; es existieren keine Π-Faktoren, denn mit $n=r=3$ gilt $p=n-r=0$. Es kann nur gelten:

${\frac {s}{gt^{2}}}={\text{const.}}$

Der Ansatz $s=f(g,t,m)$ kann nicht dimensionslos gemacht werden und ist folglich physikalisch nicht korrekt. Eine Abhängigkeit des Fallwegs von der Masse führt erst dann zu einer richtigen Beschreibung, wenn die Luft berücksichtigt wird. Denn die für die bremsende Reibung verantwortliche Luftdichte enthält die Dimension der Masse.

Galilei stand die Differentialrechnung nicht zur Verfügung. Ihm war unbekannt, dass die Fallgeschwindigkeit $v$ die zeitliche Ableitung des Fallwegs $s$ ist. Zeitweilig nahm er an, dass $s\sim v$. Hätte er sich der Dimensionsanalyse bedient, wäre klar gewesen, dass der Ansatz $s=f(v,g)$ zu

${\frac {sg}{v^{2}}}={\text{const.}}$

führt und dies ohne Kenntnis der Differentialrechnung.

Eulers Knickstab

Vertikal belastete Stäbe einer bestimmten Länge sind knickgefährdet, d. h. ihr Versagen erfolgt häufig, bevor die eigentliche Bruchlast des Querschnitts erreicht ist. Die so genannte Knicklast $F$ eines solchen Stabes mit Rechteckquerschnitt hängt vom Elastizitätsmodul $E$, seiner Länge $l$, seiner Querschnittshöhe $h$, seiner Querschnittsdicke $d$ und den Lagerbedingungen an den Enden ab:

$F=f(E,l,h,d)\,$.

Die 4 Eulerfälle mit folgenden Randbedingungen (v. l. n. r.): (1) eingespannt/frei, (2) gelenkig/gelenkig, (3) eingespannt/gelenkig, (4) eingespannt/eingespannt

Die Dimensionsmatrix $A$ für den zweiten Fall der nebenstehenden Abbildung ergibt sich für ein {F,L,T}-System in ausführlicher Schreibweise zu

$A={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\E&1&-2&0\\l&0&1&0\\h&0&1&0\\d&0&1&0\\\end{pmatrix}}$

bzw. in mathematisch exakter Formulierung zu

$A={\begin{pmatrix}1&-2&0\\0&1&0\\0&1&0\\0&1&0\\\end{pmatrix}}$.

Der Rang von $A$ ist $r:=\mathrm {rg} (A)=2$. Die Anzahl der Π-Faktoren ergibt sich mit $n=4$ und $r=2$ zu $p=n-r=2$. Bei diesen beiden leicht zu erratenden Π-Faktoren handelt es sich um die so genannten geometrischen Ähnlichkeiten $\Pi _{1}=hl^{-1}$ und $\Pi _{2}=hd^{-1}$. Für dimensionsloses $F$ muss

${\frac {F}{E\cdot l^{2}}}=G\left({\frac {h}{l}},{\frac {h}{d}}\right)$

gelten, womit die Dimensionsanalyse gezeigt hat, dass man in Laborversuchen lediglich die so genannte Schlankheit des Stabes $hl^{-1}$ und das Seitenverhältnis des Querschnitts $hd^{-1}$ variieren muss, um für beliebige E-Moduln von Rechteckstäben deren Knicklast zu erhalten.

Nach Gleichung 6 im Abschnitt Existenz und Anzahl von Π-Faktoren lässt sich ein weiterer Π-Faktor bilden:

$\Pi _{3}=\Pi _{1}\cdot \Pi _{2}^{-1}={\frac {h}{l}}\cdot {\frac {1}{\frac {h}{d}}}={\frac {d}{l}}$.

Mithilfe dieses Faktors liefert die Dimensionsanalyse die gleichwertige Beziehung

${\frac {F}{E\cdot l^{2}}}=G\left({\frac {h}{l}},{\frac {d}{l}}\right)$.

Häufig liegt es nahe, $G$ als ein Produkt der Π-Faktoren anzusetzen. Für dieses Beispiel gelangt man damit zur Gleichung

${\frac {F}{E\cdot l^{2}}}=C\cdot \left({\frac {h}{l}}\right)^{3}\cdot {\frac {d}{l}}$,

die der exakten, von Leonhard Euler aufgestellten Beziehung

$F={\frac {\pi ^{2}}{12}}\cdot {\frac {E\cdot h^{3}\cdot d}{l^{2}}}$

analog, d. h. von gleicher funktionaler Gestalt ist. Die Knicklast lässt sich in Versuchen an Stäben beliebiger Länge und Elastizität, und nicht nur auf die Rechteckform beschränkt, leicht verifizieren und in Diagrammform dargestellten. Die Kenntnis geschlossener Formeln, wie etwa der von Euler, ist nicht nötig. Bemerkenswert ist die gewonnene Erkenntnis, dass Elastizitätsmodul und Länge eines feststehenden Querschnitts für einen Knickversuch prinzipiell frei wählbar sind. Die Proportionalität zwischen $F$, $E$ und $l$ ist nach der Dimensionsanalyse bekannt.

In Fluiden umströmte Körper

Strömungswiderstand einer Kugel

Das Standardproblem in der Anfangszeit der Strömungsmechanik war die Bestimmung des Widerstands eines in einem Fluid umströmten Körpers. Dieses lässt sich mit Hilfe der Dimensionsanalyse erfassen.

Die Widerstandskraft $F$ einer Kugel und jedes anderen Körpers hängt von seiner Form, hier präzisiert durch den Kugeldurchmesser $d$, der Geschwindigkeit $v$, mit der er sich im Fluid bewegt, der Dichte $\rho$ des Mediums und dessen dynamischer Zähigkeit $\mu$ ab.

Strömungswiderstandskoeffizient einer Kugel in Abhängigkeit von der Reynolds-Zahl. Bei kleinen Re und damit niedrigen Geschwindigkeiten gilt das Stokes-Gesetz. Die Darstellung ist dimensionslos.

Gesucht ist der funktionale Zusammenhang $F=f(v,\rho ,\mu ,d)$.

Die Dimensionsmatrix $A$ in einem {M,L,T}-System ist:

$A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\v&0&1&-1\\\rho &1&-3&0\\\mu &1&-1&-1\\d&0&1&0\\\end{pmatrix}}\,{\text{bzw.}}\,A={\begin{pmatrix}0&1&-1\\1&-3&0\\1&-1&-1\\0&1&0\\\end{pmatrix}}$

Der Rang von $A$ ist 3. Es gibt $p=n-r=4-3=1$ Π-Faktor, die berühmte Reynolds-Zahl, benannt nach dem Erkenner dieses Prinzips, Osborne Reynolds und damit:

${\frac {F}{\rho \cdot v^{2}\cdot d^{2}}}=G\left({\frac {v\cdot d\cdot \rho }{\mu }}\right)=G(Re)$

Für $G(Re)$ wird üblicherweise mit sinnvoll erscheinenden Zahlenkonstanten zu $C_{D}$ umformuliert, wobei die Konvention ist, dass $d^{2}$ durch die Stirnfläche des Körpers ersetzt wird und der Proportionalitätsfaktor 1/2 aus dem Staudruck zugefügt wird. Auch mit dieser Umformulierung gilt der Zusammenhang $C_{D}=C_{D}(Re)$

Die gesuchte Widerstandskraft ist:

$F=C_{D}\cdot {\frac {1}{2}}\rho v^{2}\cdot {\frac {d^{2}\pi }{4}}$

$C_{D}$ wird als Strömungswiderstandskoeffizient bezeichnet. Er kann durch Versuche bestimmt werden und ist, wie im dimensionslosen Diagramm zu erkennen, geschwindigkeitsabhängig und keinesfalls konstant. Mit dem durch Messungen ermittelten Zusammenhang zwischen $C_{D}$ und $Re$ kann auf Kugeln mit anderem Durchmesser d und andere Fluide umgerechnet werden.

Zu Beginn bei niedrigen $Re$ gilt das analytisch schwer herzuleitende lineare Stokes-Gesetz. Anschließend, bei höheren Geschwindigkeiten, variiert $C_{D}$, bedingt durch Wirbelbildung auf der Kugelrückseite. Ähnliche Diagramme lassen sich mit Versuchen für beliebige geometrische Formen und Körper ermitteln.

Modelle von Schiffen

Skizze Schiffsmodell

Modellversuch eines F-18-Jets im Wasser. Da die Dichte des Wassers etwa 800 mal so groß ist wie die der Luft, die Viskosität aber nur um einen Faktor von ca. 100, erreichen auch kleine Modelle bei geringen Anströmgeschwindigkeiten gleiche Reynolds-Zahlen wie Flugzeuge in der Luft und ermöglichen mit begrenztem Aufwand realistische Simulationen.

Ein Schiff wird als Modell im kleinen Maßstab 1:100 untersucht.

Der Prototyp, also das echte Schiff, besitzt die Länge $L$ und die Breite $D$. Sein Tiefgang ist $t$ und es fährt mit der Geschwindigkeit $v$. Das Wasser besitzt die Dichte $\rho$ und die dynamische Zähigkeit $\mu$. Der Vorgang unterliegt der Erdbeschleunigung $g$, denn an der Wasseroberfläche entstehen dem Gesetz der Schwerkraft unterliegende Wellen. Das Wasser ist ausreichend tief gegenüber $t$.

Untersucht wird der Strömungswiderstand in Fahrtrichtung, gemessen durch eine Kraft $F$. In die Dimensionsmatrix dürfen nur unabhängige Variablen eingehen. Da etwa die Wichte $\gamma =\rho \cdot g$ ist, sind als Eingangsgrößen in $A$ nur zwei dieser drei Variablen zulässig.

Gesucht wird der funktionale Zusammenhang $F=f(v,g,\rho ,\mu ,L,D,t)$

Die Dimensionsmatrix $A$ in einem {M,L,T}-System stellt sich dar als:

$A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\v&0&1&-1\\g&0&1&-2\\\rho &1&-3&0\\\mu &1&-1&-1\\L&0&1&0\\D&0&1&0\\t&0&1&0\\\end{pmatrix}}\,\,{\text{bzw.}}\,A={\begin{pmatrix}0&1&-1\\0&1&-2\\1&-3&0\\1&-1&-1\\0&1&0\\0&1&0\\0&1&0\\\end{pmatrix}}$

Der Rang von $A$ ist 3. Für die Anzahl $p$ der Π-Faktoren gilt $p=n-r=7-3=4$. Mit Erfahrung in der Strömungsmechanik errät man:

$\Pi _{1}={\frac {L}{D}}\,$, $\Pi _{2}={\frac {t}{D}}\,$ , $\Pi _{3}=Re={\frac {\rho \cdot v\cdot D}{\mu }}\,$, $\Pi _{4}=Fr={\frac {v^{2}}{g\cdot D}}$

$\Pi _{1}$ und $\Pi _{2}$ sind geometrische Ähnlichkeiten. Maßstabsgetreu wiedergegebene Rundungen der Schiffsform werden vorausgesetzt. $\Pi _{3}$ ist die Reynolds-Zahl und $\Pi _{4}$ die Froude-Zahl.

Der dimensionslose Zusammenhang

${\frac {F}{g\cdot \rho \cdot L\cdot D\cdot t}}=G\left({\frac {L}{D}},{\frac {t}{D}},Re={\frac {\rho \cdot v\cdot D}{\mu }},Fr={\frac {v^{2}}{g\cdot D}}\right)$

ist gültig.

Vollständige Modellähnlichkeit ist erreicht, wenn alle Π-Faktoren in Modell und Prototyp konstant gehalten werden können. Bei $\Pi _{1}$ und $\Pi _{2}$ ist dies trivial. Im Wasser bleiben $\rho$ und $\mu$ unverändert. Die Konstanz der Reynolds-Zahl $Re$ erfordert die Geschwindigkeit $v$ um den Maßstabsfaktor 100 zu vergrößern, da $D$ um 100 verkleinert wurde.

• Dilemma: In die Froude-Zahl $Fr$ geht die Geschwindigkeit $v$ im Quadrat ein. Für die Konstanz von $Fr$ wäre die Erdbeschleunigung $g$ anzupassen, was ohne Zentrifuge auf der Erde nicht realisierbar ist. Vollständige Modellähnlichkeit ist nicht zu erreichen, nur $Re$ oder $Fr$ können konstant sein. Alternativ kann das Modell in einer anderen Flüssigkeit mit entsprechender Dichte und Zähigkeit untersucht werden.
• Fazit: Spielt sowohl $Fr$ als auch $Re$ eine Rolle, wird im Regelfall keine vollständige Modellähnlichkeit erreicht. Sehr kleine Modelle verlangen außerdem große Anströmgeschwindigkeiten. Viele Modelle sind deshalb nur realistisch, wenn sie entsprechend groß sind.

Modelle von Flugzeugen und U-Booten

Bei Strömungsvorgängen, in denen die freie Oberfläche des Fluids keine Rolle spielt, ist die Froude-Zahl mangels Oberflächenwellenbildung nicht relevant. Modelle von U-Booten oder Flugzeugen (unterhalb der Schallgeschwindigkeit) können im Prinzip bei vollständiger Modellähnlichkeit untersucht werden. Entscheidend ist nur die Reynolds-Zahl.

Um riesige, nicht realisierbare Strömungsgeschwindigkeiten im Windkanal zu umgehen, werden Flugzeugmodelle oft in dichteren Medien angeströmt. Bewegt sich ein Objekt so schnell, dass der Kompressionsmodul $K$ des Fluids von Belang ist, kommt die Mach-Zahl ${\mathit {Ma}}$ ins Spiel. Dann gilt die Beziehung $F=f(v,\rho ,\mu ,K,L,D,T)$. $L$ und $D$ sind charakteristische Abmessungen. Ergebnis sind drei bereits bekannte und ein neuer Π-Faktor:

$\Pi _{1}={\frac {L}{D}}\,$, $\Pi _{2}={\frac {t}{D}}\,$ , $\Pi _{3}=Re={\frac {\rho \cdot v\cdot D}{\mu }}\,$, $\Pi _{4}={\mathit {Ma}}={\frac {v}{\sqrt {\frac {K}{\rho }}}}$

Der Nenner von ${\mathit {Ma}}$ ist die Geschwindigkeit von Longitudinalwellen in elastischen Medien, in Luft die sogenannte Schallgeschwindigkeit. Die Mach-Zahl ist ab Werten von etwa ${\mathit {Ma}}=0{,}8$ von Einfluss. $K$ ist in Gasen stark druck- und temperaturabhängig.

Energie des ersten Atombombentests 1945 in New Mexico

Ein berühmtes Beispiel für die Anwendung der Dimensionsanalyse stammt vom britischen Physiker Geoffrey Ingram Taylor. Nachdem er eine Bilderserie mit genauen Zeitintervallen der ersten Atombombenexplosion 1945 in New Mexico erhalten hatte (Trinity-Test), konnte er die freigesetzte Energie der dortigen Nuklearexplosion ermitteln. Die vor Ort gemessene Sprengkraft war von den Entwicklern in Los Alamos gegenüber den außenstehenden Briten geheim gehalten worden.

Trinity-Explosion in New Mexico

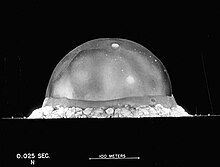
Durch frühere Überlegungen zu diesem Thema war Taylor klar, dass der Radius $R$ der anfangs etwa halbkugelförmigen Explosion maßgeblich von der Zeit $t$ seit dem Zünden der Bombe, der Dichte $\rho$ der die Explosion umgebenden Luft und natürlich von der freigesetzten Energie $E$ der Bombe abhängt. Andere Größen sind vernachlässigbar.

Damit gilt: $R=f(t,\rho ,E)$

und:

$A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\t&0&0&1\\\rho &1&-3&0\\E&1&2&-2\\\end{pmatrix}}\,{\text{bzw.}}\,A={\begin{pmatrix}0&0&1\\1&-3&0\\1&2&-2\\\end{pmatrix}}$

Der Rang von $A$ ist 3 und $p=n-r=3-3=0$. Der funktionale Zusammenhang ist bis auf eine Konstante $c$ bestimmt, denn es kann nur gelten:

${\frac {R^{5}\cdot \rho }{E\cdot t^{2}}}=c^{5}\to R(t)=c\cdot {\sqrt[{5}]{\frac {E\cdot t^{2}}{\rho }}}\to E(R,t)={\frac {R^{5}\cdot \rho }{c^{5}\cdot t^{2}}}$

Bei einer geschätzten Temperatur zum Explosionszeitpunkt um etwa 6 Uhr morgens in New Mexico von $T=20\ ^{\circ }C$ ergibt sich für die Luftdichte: $\rho =1{,}204\,\mathrm {kg/m} ^{3}$.

Der Radius $R$ ist zum Zeitpunkt $t=0{,}025\,\mathrm {s}$ im obigen Bild etwa $R=130\,\mathrm {m}$.

Der Proportionalitätsfaktor $c$ ließe sich aus einer Vergleichsexplosion mit konventionellem Sprengstoff (mehrere kg TNT) bestimmen. Taylor besaß genug Hintergrundwissen, um $c\approx 1{,}0$ annehmen zu können. Damit ist:

$E={\frac {130^{5}\cdot 1{,}204}{1{,}0^{5}\cdot 0{,}025^{2}}}=7{,}15\cdot 10^{13}\,\mathrm {J}$

1 Tonne TNT besitzt eine Energie von 4,18 Milliarden Joule. Dies führt zur Abschätzung:

$E={\frac {7{,}15\cdot 10^{13}}{4{,}18\cdot 10^{9}}}=17.095\,{\text{Tonnen TNT}}$

Trinity hatte nach offiziellen Angaben eine Energie von annähernd 19.000–21.000 Tonnen TNT. Die Abweichung zu oben erklärt sich dadurch, dass der Radius $R$ in der 5. Potenz eingeht. Das Ergebnis ist bemerkenswert genau. Taylor selbst errechnete ca. 19.000 Tonnen TNT.

Literatur

• H. L. Langhaar: Dimensional Analysis and Theory of Models., 166 p., John Wiley & Sons, New York London 1951, ISBN 0-88275-682-6.
• Henry Görtler: Dimensionsanalyse, Theorie der physikalischen Dimensionen mit Anwendungen. Springer-Verlag, Heidelberg 1975, ISBN 3-540-06937-2.
• W. J. Duncan: Physical Similarity and Dimensional Analysis. Edward Arnold & Co., London 1951, ISBN 0-7131-3042-3.
• Wilfred E. Baker, Peter S. Westine, Franklin T. Dodge: Similarity Methods in Engineering Dynamics, Theory and Practice of Scale Modeling. Second Edition, Elsevier Science Publishers, Amsterdam 1991 (Neuauflage), ISBN 0-444-88156-5.
• Joseph H. Spurk: Dimensionsanalyse in der Strömungslehre. Springer, Berlin 1999, ISBN 3-540-54959-5.
• Jochem Unger / Stephan Leyer: Dimensionshomogenität. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-05411-3
• Edgar Buckingham: On Physically Similar Systems. Illustrations of the Use of Dimensional Equations. In: Physical Review. Series II. Band 4, Nr. 4. American Physical Society, Oktober 1914, S. 345–376, doi:10.1103/PhysRev.4.345. 
• Edgar Buckingham: The Principle of Similitude. In: Nature. Band 96, Nr. 2406, 9. Dezember 1915, S. 396–397, doi:10.1038/096396d0 (nature.com [PDF; abgerufen am 1. Juni 2012]). 
• Helmut Kobus: Anwendung der Dimensionsanalyse in der experimentellen Forschung des Bauingenieurwesens. In: Die Bautechnik. Heft 3, Ernst & Sohn, Berlin 1974.

Weblinks

• Artikel über die Arbeit von Geoffrey Ingram Taylor In: Physics Today. (englisch)
• Aerospaceweb, mit Darstellungen von Strömungswiderständen mittel Ähnlichkeitskennzahlen. (englisch)
• Dimensionsanalytische Methoden zur Optimierung zerstäubungstechnischer Prozesse in der Verfahrenstechnik (PDF; 246 kB)
• An exploration of physics by dimensional analysis. (englisch)