Autonome Differentialgleichung
Als autonome Differentialgleichung oder autonomes System bezeichnet man einen Typ von gewöhnlichen Differentialgleichungen, der nicht explizit von der unabhängigen Variable abhängt.
Zum Beispiel ist die Differentialgleichung für den harmonischen Oszillator
autonom, die Mathieusche Differentialgleichung
dagegen nicht, da sie explizit von der unabhängigen Variable abhängt (ein Parameter wird „von außen“ periodisch verändert).
Die unabhängige Variable steht in den Anwendungen häufig für die Zeit.
Definition[Bearbeiten | Quelltext bearbeiten]
Eine gewöhnliche Differentialgleichung
heißt autonome Differentialgleichung, wenn die Funktion nicht explizit von der unabhängigen Variable abhängt, das heißt wenn
für alle im Definitionsbereich gilt.
Diese Differentialgleichung -ter Ordnung kann auch als ein System aus Differentialgleichungen erster Ordnung geschrieben werden – dazu führt man neue Variablen
- mit
und
- (die gesuchte Funktion)
ein.
Dadurch erhält man ein System von gekoppelten Differentialgleichungen für gesuchte Funktionen.
Das System der Differentialgleichungen kann man geometrisch interpretieren als System erster Ordnung in einem n-dimensionalen Phasenraum gegeben durch :
Die Differentialgleichung bestimmt die Tangenten der Lösungskurven im Phasenraum. Ein solches System gekoppelter autonomer gewöhnlicher Differentialgleichungen erster Ordnung kann aber auch direkt in den Anwendungen vorgegeben sein. Für die qualitative Diskussion von Bedeutung sind die Fixpunkte, an denen die Ableitung verschwindet (siehe unten).
Die Lösungen der autonomen Differentialgleichungen sind translationsinvariant. Ist eine Lösung einer autonomen Differentialgleichung, so ist auch für alle eine Lösung ebendieser Gleichung bei geeignet verschobener Anfangsbedingung.
In vielen Anwendungen ist die unabhängige Variable die Zeit .
Ein nicht-autonomes System in Variablen , in dem noch explizit von der unabhängigen Variablen abhängt, kann man durch Hinzufügung einer weiteren Variablen mit
formal autonom machen.[1] Damit erhält man
- .
Lösungsmethoden[Bearbeiten | Quelltext bearbeiten]
Die Gleichung erster Ordnung (die unabhängige Variable ist im Folgenden )
kann durch Trennung der Variablen gelöst werden, formal:
mit einer Konstanten . Bei Gleichungen zweiter Ordnung kann man häufig wie oben nach Einführung neuer Variabler ebenfalls durch Trennung der Variablen lösen. Sei
mit der neuen Variablen
- (Gleichung 1)
und
erhält man:
- (Gleichung 2)
Das ist ein gekoppeltes System von zwei Gleichungen (Gleichung 1,2). Wendet man in der Gleichung 1 Trennung der Variablen an erhält man:
Für muss man die Gleichung 2 lösen. Ist
kann man dort ebenfalls Trennung der Variablen ausführen und erhält:
und insgesamt:
Ebenfalls mit Trennung der Variablen kann man den Fall:
behandeln, wie man durch Einsetzen in die Gleichung 2 sieht.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Autonome Systeme kommen häufig in der Theorie Dynamischer Systeme vor. Ein Beispiel für eine autonome Differentialgleichung ist die in der theoretischen Biologie verwendete logistische Differentialgleichung und der Lorenz-Attraktor in der Chaostheorie. Beide sind nichtlinear. In der Hamiltonschen Mechanik (mit klassischem Phasenraum aus Orts- und Impulsvariablen) hat man es mit solchen Systemen zu tun falls die Hamiltonfunktion nicht explizit zeitabhängig ist.
Das Umschreiben eines nicht-autonomen Differentialgleichungssystems in ein autonomes Differentialgleichungssystem wird als Autonomisierung bezeichnet.
Qualitative Theorie der Fixpunkte der Differentialgleichung[Bearbeiten | Quelltext bearbeiten]
Als Fixpunkt (Gleichgewichtspunkt) der Differentialgleichung, betrachtet als Vektorfeld (Fluss) im Phasenraum (die Tangenten der Trajektorien (Bahnen) sind ) bezeichnet man eine Stelle , an der die autonome gewöhnliche Differentialgleichung (unabhängige Variable sei die Zeit t, ein tiefgestellter Index stellt eine Ableitung dar) eine Nullstelle hat:[2]

An diesem Punkt ist das dynamische System stationär (zeitunabhängig). Ein Fixpunkt ist stabil, falls Trajektorien aus einer Umgebung des Fixpunkts in der Umgebung bleiben, und asymptotisch stabil, falls Trajektorien aus einer Umgebung (die maximale Erweiterung ist das Einzugsgebiet (Basin of attraction) des Fixpunkts) für gegen den Fixpunkt konvergieren, ein Fall, der häufig bei Problemen mit Dämpfung auftritt. Das ist ein Beispiel eines Attraktors. Es gibt auch kompliziertere Attraktoren zum Beispiel mit Grenzzyklus, hier werden nur solche vom Typ isolierter Punkte betrachtet.
Man linearisiere um den Fixpunkt
- :
mit Termen höherer Ordnung in , die vernachlässigt werden, und einer Matrix , der Jacobi-Matrix:
- (ausgewertet an der Stelle )
so dass der Fall einer konstanten, als nicht-singulär angenommenen Matrix vorliegt. Der Einfachheit wird hier nur der ebene Fall behandelt . Dann hat die Matrix , da sie reell ist, die beiden komplex konjugierten Eigenwerte , die aus der charakteristischen Gleichung bestimmt werden:
ausgedrückt durch die Determinante und Spur der Matrix . Die Lösung der linearisierten Gleichung ist:
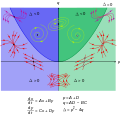
- Der Fall asymptotischer Stabilität (Abbildung rechts) liegt dann für vor (beide Eigenwerte negativer Realteil). Das entspricht genau dem Fall, dass und Im Phasenbild liegt eine Senke (stabiler Knoten) vor. In der Abbildung hat sie Spiralform (das heißt die Eigenwerte sind nicht reell, sondern haben nicht verschwindenden Imaginärteil), was auch Fokus genannt wird[3], sind sie reell liegt ein Knoten vor.
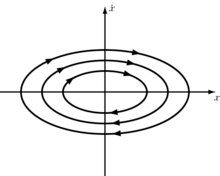
- Für (also rein imaginäre Eigenwerte) hat man den Fall neutraler Stabilität, zum Beispiel die periodische Bewegung eines Pendels (das Phasenbild hat eine Zentrums-Mannigfaltigkeit, elliptischer Fixpunkt). Das entspricht das .
- Falls nur für einen der Eigenwerte ist, sind alle Eigenwerte reell und der zweite Eigenwert ist positiv. Das entspricht dem Fall . Hier hat man einen Sattelpunkt. Der Phasenraum der Differentialgleichung wird beim Sattelpunkt durch zwei sich kreuzende Geraden (Separatrix) in vier Bereiche aufgeteilt, in denen die Trajektorien jeweils bleiben. Auf der einen Geraden verläuft die Bahn für zum Fixpunkt (stabile Untermannigfaltigkeit), auf der anderen vom Fixpunkt fort (Instabile Untermannigfaltigkeit), das heißt für zum Fixpunkt. Da sie den Fixpunkten nur für unendliche Zeiten erreichen, schneiden sich die zu den Geraden gehörigen Trajektorien nicht.

- Für hat man keinen stabilen Fixpunkt: die Trajektorien streben vom Punkt weg. Hier liegt ein instabiler Knoten (Quelle) vor bzw. bei nicht-verschwindendem Imaginärteil der Eigenwerte ein instabiler Fokus. Das entspricht dem Fall und .
Die Diskussion für den linearisierten Fall gilt lokal. Für sogenannte Hyperbolische Fixpunkte[4], für die die Realteile der Eigenwerte des linearisierten Systems ungleich Null sind (worunter Quellen, Senken, Sattelpunkte und Foki (Spiralen) fallen), lässt sich aus dem linearisierten Verhalten auf das Verhalten des nichtlinearen Systems nahe dem Fixpunkt schließen (Satz von Hartman-Grobman).
Man unterscheidet zwischen konservativen Systemen, in denen für die Geschwindigkeiten
gilt (zum Beispiel Hamiltonsche Systeme ohne Zeitabhängigkeit der Hamiltonfunktion nach dem Satz von Liouville) und solchen, in denen dies nicht gilt (dissipative Systeme). Bei konservativen Systemen, in denen das Phasenraumvolumen erhalten ist, gibt es als Fixpunkte nur elliptische Fixpunkte (Zentren) und Sattelpunkte (nicht Quellen, Senken oder Spiralen), und Grenzzyklen sind auch nicht erlaubt. Grenzzyklen sind als mögliche Grenzmengen des Phasenraumflusses zuerst von Henri Poincaré betrachtet worden (der für zwei Dimensionen geltende Satz von Poincaré-Bendixson macht hier Existenzaussagen). Grenzzyklen können bei Variation der Parameter des Systems durch Hopf-Bifurkation aus Fixpunkten entstehen (das entspricht dem Fall, dass und ). Bei einer Sattel-Knoten-Bifurkation kollidieren zwei Fixpunkte. Das entspricht dem Übergang von nach (von Knoten zu Sattelpunkten und umgekehrt).
In drei Dimensionen hat man drei Eigenwerte und je nachdem deren Real- und Imaginärteil verschwindet, positiv oder negativ ist mehr Möglichkeiten: zum Beispiel neben Sattel und Knoten wie oben stabile und instabile Fokus-Knoten und Sattel-Foki.[5] Es gibt auch neue Arten nicht-hyperbolischer Fixpunkte, die bei Zuschalten der nichtlinearen Terme nicht strukturell stabil sind. Deren Verhalten hängt vielmehr von den nichtlinearen Termen ab und es entstehen neue Typen nicht-hyperbolischer Fixpunkte etwa bei Hopf-Bifurkationen oder Sattel-Knoten-Bifurkationen. Zum Beispiel tritt die Bogdanov-Takens-Bifurkation in nichtlinearen Systemen auf, in denen zwei der Eigenwerte verschwinden (sie besteht aus einer Kombination von Sattel-Knoten-Bifurkation und Hopf-Bifurkation).
Galerie[Bearbeiten | Quelltext bearbeiten]
-
Qualitatives Verhalten nahe der Fixpunkte in zwei Dimensionen in Abhängigkeit von Spur p und Determinante q
-
Phasendiagramme des Pendels mit durchgehender blauer Separatrix mit Sattelpunkten in den scheinbaren Schnittpunkten. Die Separatrix umhüllt die geschlossenen Kurven (periodische Bewegung mit Zentrum)
Literatur[Bearbeiten | Quelltext bearbeiten]
- Günther Wirsching: Gewöhnliche Differentialgleichungen, Teubner 2006
- Hirsch, Smale, Devaney: Differential Equations, Dynamical Systems and Introduction to Chaos, Academic Press 2004
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Autonomous, Wolfram Mathworld
- ↑ Darstellung im Folgenden nach Beltrami, Mathematics for Dynamics Modeling, Academic Press 1987. Auch dargestellt in Hirsch, Smale, Differential Equations, Dynamical Systems and Linear Algebra, Academic Press 1974 und der Neuauflage Hirsch, Smale, Devaney, Differential Equations, Dynamical Systems and Introduction to Chaos, Academic Press 2004, dort Klassifikation ebener Systeme nach Determinante und Spur der Matrix zusammengefasst in der Abbildung S. 63
- ↑ Fixpunkte, Spektrum Lexikon der Physik
- ↑ Manchmal wird auch im engeren Sinn ein Sattelpunkt als hyperbolischer Fixpunkt, der Fall eines Zentrums als elliptisch bezeichnet, siehe das oben zitierte Spektrum Lexikon der Physik.
- ↑ Siehe die Abbildungen in Eugene M. Izhikevich, Equilibrium, Scholarpedia

![{\displaystyle y''(x)+[\lambda +\gamma \cos(x)]\cdot y(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/249913336cbd31556b47a6fe7c54b3738bda0dec)