Born-Koordinaten

Abb. 1: Die Raumzeit der Born-Koordinaten im Minkowski-Raum (Zylinderkoordinaten). Die roten Linien ( | ) sind die Weltlinien der ruhenden Punkte auf der rotierenden Scheibe. Die wechselnden grauen und blauen Streifen zeigen Flächen mit konstanter Zeit $T$. Die orangefarbenen Linien (/ \) zeigen lichtartige Kurven mit konstanten $R,\,T$ und $\Phi$.

Die Born-Koordinaten beschreiben in der relativistischen Physik eine Karte für einen Teil des flachen Minkowski-Raumes der speziellen Relativitätstheorie, den räumlichen Zylinder mit $r<1/\omega .$ Das entsprechende Linienelement mit der Signatur $(1,3)$, also $(+,-,-,-),$ den natürlichen Einheiten $G=c=1$ und der Winkelgeschwindigkeit $\omega$ ist

$\mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},$

$-\infty <t{,}\,z<\infty {,}\quad 0<r<1/\omega {,}\quad -\pi \leq \phi <\pi .$

Die Born-Koordinaten werden für die mathematische Analyse der Physik von sogenannten Langevin-Beobachtern benutzt, die auf einem Ring mit konstantem Abstand zum Drehmittelpunkt rotierender starrer Scheiben ruhen (siehe Ehrenfestsches Paradoxon). Die erstmalige Beschreibung dieser Koordinaten erfolgte im Zusammenhang mit Max Borns (1909) relativistischer Physik der starren Körper, die für rotierende Körper unter anderem von Gustav Herglotz (1909) weiterentwickelt wurde. Für einen allgemeinen Überblick zu Beschleunigungen in der Minkowski-Raumzeit, siehe Beschleunigung (Spezielle Relativitätstheorie).

Uhrensynchronisation und Abstandsmessung

Abb. 2: Die Animation zeigt die Synchronisation der Uhren bei ${\rm {A}}$, ${\rm {B}}$ und ${\rm {L}}$ auf dem Ring mit dem Radius $r=1$ und etwa 62 % der Lichtgeschwindigkeit auf einer rotierenden Scheibe mit der zentralen Uhr ${\rm {O}}$ im Rotationsmittelpunkt als Referenz. Die so synchronisierten Uhren ${\rm {A}}$, ${\rm {B}}$, ${\rm {L}}$ und ${\rm {O}}$ zeigen die Koordinatenzeit $t$ des Inertialsystems im Minkowskiraum, in dem die Drehachse der Scheibe ruht. Die gepunkteten Linien zeigen den Weg der Lichtstrahlen (Nullgeodäten) im Inertialsystem. Die farbigen Linien die entsprechenden Nullgeodäten im Bezugssystem der rotierenden Scheibe. Die grünen Linien sind die auslaufenden radialen Nullgeodäten. Sie sind in Drehrichtung gebogen. Die blauen Linien sind die einlaufenden radialen Nullgedäten. Sie sind gegen die Drehrichtung gebogen. Zu beachten ist, dass auslaufende und einlaufende radiale Nullgedäten nicht den gleichen Weg nehmen. Die violette Kurve zeigt die nach außen gebogene Nullgedäte von ${\rm {A}}$ nach ${\rm {L}}$, die rote Kurve, die nach innen gebogene Nullgeodäte von ${\rm {B}}$ nach ${\rm {L}}$. Die bei ${\rm {A}}$ und ${\rm {B}}$ gleichzeitig (bezüglich des Inertialsystems) abgesendeten Lichtstrahlen kommen nicht gleichzeitig beim Langevin-Beobachter in ${\rm {L}}$ an. Für diesen sind die Uhren ${\rm {A}}$ und ${\rm {B}}$ nicht synchron.

Ideale ruhende Uhren auf der rotierenden Scheibe lassen sich nicht widerspruchsfrei synchronisieren. Nicht auf einem Ring mit konstantem Durchmesser auf dem die Uhren zumindest gleich schnell laufen, schon gar nicht auf der ganzen Scheibe, auf der die Uhren, je weiter sie von der Drehachse entfernt sind, um den Faktor $\gamma ^{-1}=(1-\omega {^{2}}r{^{2}})$ langsamer laufen (Zeitdilatation). Das heißt, dass die Uhren entlang eines Radius mit $t=\phi =z={\rm {const.}}$ nicht gleich schnell laufen, sondern im Vergleich mit einer Referenzuhr im Drehmittelpunkt $r=0$ mit wachsendem $r>0$ langsamer werden.

Da die Born-Koordinaten einen Teil des flachen Minkowski-Raums beschreiben, lassen sich die Uhren wie dort synchronisieren, indem die Uhr im Drehmittelpunkt (Uhr ${\rm {O}}$ im Rotationszentrum) als Referenz dient und z. B. im Sekundentakt ein Lichtsignal aussendet, mit dem alle Uhren auf der rotierenden Scheibe synchronisiert werden (siehe Abb. 2). Die Empfängeruhren ${\rm {L}}$, ${\rm {A}}$ und ${\rm {B}}$ kennen die jeweilige Laufzeit des Signals vom Drehmittelpunkt und justieren ihre Uhrzeit entsprechend. Das heißt, dass alle Beobachter, die sich auf der Drehachse befinden, Lichtsignale, die von den Uhren auf der Scheibe im Sekundentakt abgesendet werden, im Sekundentakt empfangen werden. Werden die Signale von Uhren auf einem Ring mit konstantem Radius gesendet, werden sie darüber hinaus gleichzeitig empfangen. Solcherart synchronisiert, sind die Uhren in ${\rm {A}}$, ${\rm {B}}$, ${\rm {L}}$ und ${\rm {O}}$ synchron mit der Koordinatenzeit $t$ des Inertialsystems, in dem die Drehachse der rotierenden Scheibe ruht.

Für den Langevin-Beobachter (Uhr ${\rm {L}}$) ist die Situation jedoch nicht zufriedenstellend. Für ihn ergeben sich zwei Probleme. Erstens läuft seine so synchronisierte Uhr zu schnell im Vergleich zu einer Uhr, die er auf die Standard-SI-Sekunde geeicht hat. Zweitens macht er die irritierende Feststellung, dass zwei Lichtsignale, die von den beiden gleich weit entfernten Uhren ${\rm {A}}$ und ${\rm {B}}$ auf seinem Ring gleichzeitig ausgesendet werden, nicht gleichzeitig bei ihm eintreffen. Da er weiß, dass die Uhren ${\rm {A}}$ und ${\rm {B}}$ gleich weit von seiner Uhr ${\rm {L}}$ entfernt sind, gibt es nur zwei Möglichkeiten. Entweder ist die Lichtausbreitung nicht isotrop – Licht von ${\rm {A}}$ in Drehrichtung ist früher bei ihm (die Geschwindigkeit des Lichts wäre daher schneller als $c$), als Licht von ${\rm {B}}$ entgegen der Drehrichtung (die Geschwindigkeit des Lichts wäre daher langsamer als $c$). Oder die Uhren ${\rm {A}}$ und ${\rm {B}}$ sind mit seiner Uhr ${\rm {L}}$ nicht synchron.

Um sie aus seiner Sicht zu synchronisieren geht er wie im Inertialsystem vor. Er eicht die Uhren in ${\rm {A}}$, ${\rm {B}}$ und ${\rm {L}}$ auf die SI-Sekunde und synchronisiert die Uhren ${\rm {A}}$ und ${\rm {B}}$ mit seiner Uhr ${\rm {L}}$ mittels Einstein-Synchronisation (eine interne Synchronisation). Er stellt fest, dass er die Uhr ${\rm {A}}$, die in Drehrichtung liegt, zurückstellen muss und die Uhr ${\rm {B}}$, die entgegen der Drehrichtung liegt, vorstellen muss. Zwei Lichtsignale, die jetzt gleichzeitig von ${\rm {A}}$ und ${\rm {B}}$ ausgesendet werden, treffen gleichzeitig bei ${\rm {L}}$ ein (sie treffen aber nicht gleichzeitig bei der Uhr ${\rm {O}}$ ein). Synchronisiert man alle Uhren entlang des Ringes auf diese Art und Weise, ergibt sich neuerlich ein Problem. Zumindest zwei benachbarte Uhren zeigen nicht die gleiche Zeit. In Summe weisen die Uhren entlang des Rings mit dem Radius r eine Zeitdifferenz $\Delta t=(2\pi \omega r^{2})/(1-\omega ^{2}r^{2})$ auf.

Außerdem stellt der Langevin-Beobachter fest, dass, egal wie er die Distanzen seiner lokalen Umgebung vermisst, die Geometrie nicht-euklidisch ist und am besten durch eine Riemannsche Metrik, die sogenannte Langevin-Landau-Lifschitz Metrik beschrieben wird. Diese Metrik wiederum wird sehr gut durch die Metrik der hyperbolischen Ebene angenähert. Bei der Vermessung großer Distanzen über die lokale Umgebung hinaus hängen die Ergebnisse von der Messmethode ab, die sich nicht mit den Eigenschaften einer Riemann Metrik beschreiben lassen. Die mit der Radarmethode gemessenen großen Distanzen sind nicht einmal symmetrisch. Die gemessene Entfernung von ${\rm {L}}$ nach ${\rm {O}}$ ist nicht gleich der gemessenen Entfernung von ${\rm {O}}$ nach ${\rm {L}}$. Das heißt, dass die Geometrie der rotierenden Scheibe weder eine euklidische noch eine riemannsche Geometrie ist.

Die rotierende Scheibe ist kein Paradoxon. Egal welche Methode der Langevin-Beobachter verwendet um seine lokale Umgebung zu analysieren: er stellt fest, dass er sich in einem rotierenden Bezugssystem befindet und nicht in einem Inertialsystem.

Langevin-Beobachter in Zylinderkoordinaten

Für die Herleitung der Born-Koordinaten ist es sinnvoll, die Langevin-Beobachter zuerst in Zylinderkoordinaten darzustellen. Ihre Weltlinien bilden eine zeitartige Kongruenz, die als starr angesehen werden kann, da der entsprechende Expansionstensor verschwindet (siehe unten). Die Langevin-Beobachter rotieren um die Symmetrieachse des Zylinders.

Abb. 3: Darstellung der wendelförmigen Weltlinie eines Langevin-Beobachters in Zylinderkoordinaten (rote Kurve). Ebenfalls dargestellt sind die Zukunftslichtkegel (goldfarben) und die Tetraden (Basisvektoren) der lokalen Bezugssysteme (schwarze Vektoren). Der graue Zylinder ist eine Fläche mit konstantem $R$ und die grüne strichlierte Linie ist die Symmetrieachse (Drehachse) bei $R=0$. Die blaue Kurve ist eine integrale Kurve des azimutalen Vektors ${\vec {p}}_{3}$. Die $Z$-Koordinate ist für diese Darstellung unwesentlich und wird weggelassen.

Aus dem Linienelement des Minkowskiraumes in Zylinderkoordinaten

${\begin{aligned}&\mathrm {d} s^{2}=\mathrm {d} T^{2}-\mathrm {d} Z^{2}-\mathrm {d} R^{2}-R^{2}\,\mathrm {d} \Phi ^{2},\;\;\\&-\infty <T,\;Z<\infty ,\quad 0<R<\infty ,\quad -\pi \leq \Phi <\pi ,\end{aligned}}$

können unmittelbar die Tetraden (Vektorfelder der Basisvektoren) des lokalen Bezugssystems für stationäre Beobachter abgelesen werden:

${\vec {e}}_{0}=\partial _{T},\;\;{\vec {e}}_{1}=\partial _{Z},\;\;{\vec {e}}_{2}=\partial _{R},\;\;{\vec {e}}_{3}={\frac {1}{R}}\,\partial _{\Phi }.$

${\vec {e}}_{0}$ ist ein zeitartiges Vektorfeld. ${\vec {e}}_{1}$, ${\vec {e}}_{2}$ und ${\vec {e}}_{3}$ sind raumartige Vektorfelder.

Mit einem Lorentz-Boost der Vektorfelder der Basisvektoren mit $\omega R$ in Richtung ${\vec {e}}_{3}$ (Anwendung der Lorentz-Transformation auf ${\vec {e}}_{3}$ und ${\vec {e}}_{0}$) ergeben sich die Vektorfelder der Basisvektoren für die Langevin-Beobachter mit

${\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\partial _{\Phi },$

${\vec {p}}_{1}=\partial _{Z},\;\;{\vec {p}}_{2}=\partial _{R},$

${\vec {p}}_{3}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\,\partial _{\Phi }+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}.$

Diese Vektorfelder wurden erstmals (implizit) von Paul Langevin 1935 verwendet. Eine ausführliche Beschreibung erfolgte durch Thomas A. Weber erst 1997. Definiert sind diese Vektorfelder im Gegensatz zu den Zylinderkoordinaten mit $0<R<\infty$ im Bereich $0<R<1/\omega$. Diese Einschränkung ist fundamental, da sich die Geschwindigkeit der Langevin-Beobachter nahe der Grenze $R\rightarrow 1/\omega$ der Lichtgeschwindigkeit nähert.

Abb. 4: Darstellung der Weltlinien (strichlierte blaue Kurven) der zu einem bestimmten Langevin-Beobachter (rote wendelförmige Kurve) benachbarten Beobachter. Aus der Sicht eines bestimmten Langevin-Beobachters. Die cyanfarbene Kurve stellt die Bewegung des radialen Vektorfeldes ${\vec {p}}_{2}$ (des radialen Basisvektors) für ein Viertel einer vollen Umdrehung um die Drehachse (grüne Kurve) dar.

Jede integrale Kurve des zeitartigen Vektorfeldes ${\vec {p}}_{0}$ wird in Zylinderkoordinaten als wendelförmige Kurve mit konstantem Radius abgebildet (siehe die rote Kurven in Abb. 1 und Abb. 3) und repräsentiert einen in Bezug auf die rotierende Scheibe ruhenden Langevin-Beobachter. Weitere Langevin-Beobachter, die sich mit dem ersten auf einem Ring mit dem Radius $R$ und der Winkelgeschwindigkeit $\omega$ befinden, sollten auf der integralen Kurve des Vektorfeldes ${\vec {p}}_{3}$ (siehe die blaue Kurve in Abb. 3) gleichzeitig (synchron) sein. Jedoch zeigt sich, dass sich ideale Uhren entlang der blauen Kurve mittels Einstein-Synchronisation nicht synchronisieren lassen, da sich die blaue Kurve an unterschiedlichen Stellen mit der roten Kurve schneidet. Zumindest zwei benachbarte Uhren zeigen unterschiedliche Zeiten, da die blaue Kurve gleichzeitig ist, zwei unterschiedliche Stellen auf der roten Kurve aber einen zeitlichen Abstand haben – die blaue Kurve ist keine geschlossene Kurve in der Raumzeit und die benachbarten Uhren sie sind nicht synchron. Das ist der erste Hinweis darauf, dass sich für die rotierende Scheibe keine zufriedenstellende Beschreibung einer räumlichen Geometrie finden lässt, auf der alle Ereignisse gleichzeitig sind. Weder für die ganze rotierende Scheibe, noch für einen rotierenden Ring mit Radius $R$.

Im Gegensatz dazu, ist die Projektion der wendelförmigen Weltlinie eines Langevin-Beobachters auf die räumliche Hyperebene $T=\mathrm {const.}$ ein Kreis – also eine geschlossene Kurve in der Raumzeit. Darüber hinaus ist das Vektorfeld der Basisvektoren ${\vec {e}}_{3}=(1/R)\,\partial _{\Phi }$ ein raumartiges Killingvektorfeld, dessen integrale Kurven geschlossene Kurven im Raum sind (de-facto Kreise). Sie degenerieren für $R=0$ zu Kurven mit der Länge Null. Das entspricht der Vorstellung der zylindrischen Symmetrie und der Vorstellung eines rotierenden Langevin-Beobachters. Diese Vorstellung basierend auf $T=\mathrm {const.}$ lässt sich jedoch nicht realisieren, da die idealen Uhren auf dem Ring nicht widerspruchsfrei synchronisiert werden können und damit $T=\mathrm {const.}$ (Gleichzeitigkeit) keinen Sinn ergibt, wenn keine eindeutige Synchronisation der Uhren möglich ist.

Die Viererbeschleunigung des zeitartigen Vektorfeldes ${\vec {p}}_{0}$ ist

$\nabla _{{\vec {p}}_{0}}{\vec {p}}_{0}={\frac {-\omega ^{2}\,R}{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{2}.$

Sie zeigt radial zur Drehachse und hängt nur vom konstanten Radius $R$ und der konstanten Winkelgeschwindigkeit $\omega$ der wendelförmigen Weltlinie des Langevin-Beobachters ab (Zentripetalbeschleunigung). Mit der kinematischen Dekomposition (siehe Viererbeschleunigung oben) ergeben sich der Expansionstensor und der Wirbelvektor. Der Expansionstensor ist Null. Das heißt, dass die Abstände der Langevin-Beobachter zueinander und zur Drehachse konstant bleiben (starren Scheibe). Der Wirbelvektor ergibt sich mit

${\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{1}$

und ist parallel zur Drehachse. Das heißt, dass die Langevin-Beobachter um die Drehachse rotieren. Das heißt aber auch, dass die Langevin-Beobachter um ihre eigene Achse rotieren. Das entspricht der Vorstellung einer lokalen Verwirbelung. In Abb. 4 zeigt die cyanfarbene Kurve, wie sich die raumartigen Vektorfelder ${\vec {p}}_{2},\;{\vec {p}}_{3}$ um das Vektorfeld ${\vec {p}}_{1}$ winden (${\vec {p}}_{1}$ – die $Z$-Koordinate – ist in der Abb. 4 durch ${\vec {e}}_{0}$ – die Zeit – ersetzt, da die $Z$-Koordinate hier keine Rolle spielt). Die lokalen Bezugssysteme der Langevin-Beobachter rotieren also auch und sind keine Inertialsysteme und ihre ${\vec {p}}_{2}=\partial _{R}$ sind mit dem radial Basisvektor ${\vec {e}}_{2}=\partial _{R}$ ausgerichtet. Diese lokale Rotation von ${\vec {p}}_{2}$ und ${\vec {p}}_{3}$ um die Achse ${\vec {p}}_{1}$ kann durch eine konstante lokale Gegenrotation aufgehoben werden.

Transformation in Born-Koordinaten

Abb. 5: Darstellung einer Vorstellung eines „Raumes zu einer bestimmten Zeit“ in Born-Koordinaten (einer „Gleichzeitigkeitsfläche“ oder auch einer dreidimensionale Hyperfläche). Die Fläche zeigt den Bereich $0<r<1$ mit der Winkelgeschwindigkeit $\omega =1/5.$ Ausgehend vom radialen Strahl mit $\phi =0$ (die blaue Linie rechts hinten) wird die Fläche durch die Integralkurven mit dem Tangentenvektor ${\vec {p}}_{3}$ gebildet. Diese Vorstellung eines „Raumes zu einer bestimmten Zeit“ ist jedoch zumindest aus zwei Gründen zum Scheitern verurteilt. Erstens müssten die Vektoren ${\vec {p}}_{1},\,{\vec {p}}_{2},\,{\vec {p}}_{3}$ Tangentenvektoren dieser „Gleichzeitigkeitsfläche“ sein, ${\vec {p}}_{2}=\partial _{r}$ ist jedoch nur für $\phi =0$ (mit dem Fußpunkt auf der blauen Linie) tangential. Zweitens hat die „Gleichzeitigkeitsfläche“ bei $\phi =\pi$ eine Unstetigkeit (einen „Sprung“, siehe die blauen Gitterlinien). An dieser Unstetigkeit lässt sich keine eindeutige Zeit definieren.

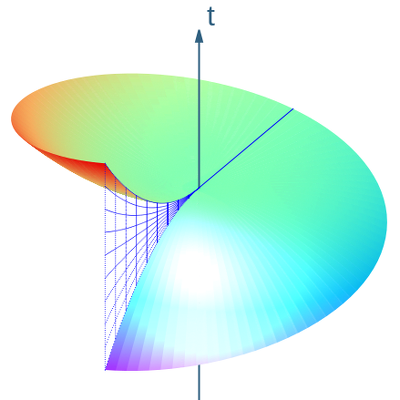
Um die Born-Koordinaten zu erhalten, werden die wendelförmigen Weltlinien der Langevin-Beobachter mittels der Transformation

$t=T,\;\;z=Z,\;\;r=R,\;\;\phi =\Phi -\omega \,T$

„gestreckt“ und es ergibt sich das neue Linienelement

$\mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},$

$-\infty <t,\,z<\infty ,\quad 0<r<{\frac {1}{\omega }},\quad -\pi <\phi <\pi .$

Wegen des Mischterms $\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi$ sind die Born-Koordinaten kein orthogonales Koordinatensystem.

Die Weltlinien der Langevin-Beobachter sind jetzt gerade vertikale Linien. In Born-Koordinaten sind die Vektorfelder der Basisvektoren der Langevin-Beobachter

${\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},$

${\vec {p}}_{1}=\partial _{z},\;\;{\vec {p}}_{2}=\partial _{r},$

${\vec {p}}_{3}={\frac {\sqrt {1-\omega ^{2}\,r^{2}}}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}.$

Die wendelförmigen Weltlinien der Langevin-Beobachter in Zylinderkoordinaten sind in Born-Koordinaten gerade Linien. Jedoch sind die geraden Weltlinien der statischen Beobachter in Zylinderkoordinaten, die neben der rotierenden Scheibe ruhen, in Born-Koordinaten wendelförmige Weltlinien. Im Gegensatz zu den Zylinderkoordinaten, sind nicht nur die Vektorfelder der Basisvektoren der Langevin-Beobachter auf den Bereich $0<r<1/\omega$ beschränkt, sondern die Born-Koordinaten insgesamt.

Die kinematische Dekomposition der zeitartigen Kongruenz $\textstyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}$ liefert die gleichen Ergebnisse wie zuvor, jedoch mit den neuen Born-Koordinaten. Der Beschleunigungsvektor ist

$\nabla _{{\vec {p}}_{0}}\,{\vec {p}}_{0}={\frac {-\omega ^{2}\,r}{1-\omega ^{2}\,r^{2}}}\,{\vec {p}}_{2},$

der Expansionstensor ist Null und der Wirbelvektor ist

${\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,r^{2}}}\;{\vec {p}}_{1}.$

Das zu einem zeitartigen Einheitsvektorfeld duale Kovektorfeld definiert in jedem lokalen Bezugssystem eine infinitesimale räumliche Hyperebene. Ob diese infinitesimalen räumlichen Hyperebenen zu einer globalen räumlichen Hyperebene verbunden werden können, die überall zur Kongruenz der Weltlinien orthogonal ist, wird durch die Bedingung für die vollständige Integrierbarkeit bestimmt. Es zeigt sich, dass diese Bedingung genau dann und nur dann erfüllt ist, wenn der Wirbeltensor Null ist. Für den statischen Beobachter in Zylinderkoordinaten existieren solche räumliche Hyperflächen für die $T=\mathrm {const.}$ gilt, für den Langevin-Beobachter jedoch nicht. Insbesondere sind die räumlichen Hyperflächen $t=\mathrm {const.}$ in Born-Koordinaten orthogonal zu den Weltlinien der statischen Beobachter, nicht zu den Weltlinien der Langevin-Beobachter.

Dies wird deutlich, wenn die Integralkurven des Langevin-Vektorfeldes

${\vec {p}}_{3}={\sqrt {1-\omega ^{2}\,r^{2}}}\,{\frac {1}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},$

die durch den Radius $\phi =0,\,t=0$ verlaufen, dargestellt werden. Diese Kurven liegen in der Fläche

$\phi +\omega \,t-{\frac {t}{\omega \,r^{2}}}=0,\;\;-\pi <\phi <\pi$

(siehe Abb. 5). Die für die Darstellung unwesentliche Koordinate $z$ wurde durch die Koordinate $t$ ersetzt. Es liegt nahe, diese Fläche als räumliche „Gleichzeitigkeitsfläche“ für Langevin-Beobachter zu interpretieren. Dies ist aus zwei Gründen nicht möglich. Erstens ist die Bedingung für die vollständige Integrierbarkeit nicht erfüllt, sodass es keine räumliche Hyperfläche gibt zu der die Vektorfelder ${\vec {p}}_{2},\,{\vec {p}}_{3}$ tangential sind. Das Vektorfeld ${\vec {p}}_{2}$ ist nur für $\phi =0$ tangential. Das ist ein infinitesimales (lokales) Problem. Zweitens wird in Abb. 5 ersichtlich, dass die so konstruierte räumliche Hyperebene eine Unstetigkeit aufweist, einen Sprung (siehe die blauen Gitterlinien Abb. 5). Das ist ein globales Problem und eine Konsequenz daraus, dass sich die Uhren der Langevin-Beobachter nicht widerspruchsfrei synchronisieren lassen. Weder auf der ganzen rotierenden Scheibe, noch auf einem Ring mit konstantem $r$.

Nullgeodäten

Abb. 6: In Zylinderkoordinaten sind die Nullgeodäten gerade Linien (grüne Kurve). In Parameterdarstellung mit dem affinen Parameter λ sind der Radius $R={\sqrt {\lambda ^{2}(E^{2}-P^{2})+R_{\mathrm {min} }^{2}}}$ und der Winkel $\Phi =\Phi _{0}+\operatorname {arctan} \left[(\lambda {\sqrt {E^{2}-P^{2}}})/(R_{\mathrm {min} }\,\operatorname {sgn} {(L)})\right]$.

Die Nullgeodäten in Zylinderkoordinaten ergeben sich aus den Geodätengleichungen

${\ddot {T}}=0,\;\;{\ddot {Z}}=0,\;\;{\ddot {R}}-R\,{\dot {\Phi }}^{2}=0,\;\;{\ddot {\Phi }}+{\frac {2}{R}}\,{\dot {\Phi }}\,{\dot {R}}=0.$

Die ersten Integrale für ${\ddot {T}},\,{\ddot {Z}},\,{\ddot {\Phi }}$ lassen sich unmittelbar angeben mit

${\dot {T}}=E,\;\;{\dot {Z}}=P,\;\;{\dot {\Phi }}={\frac {L}{R^{2}}}.$

Wird das in den Ausdruck für das Linienelement der Zylinderkoordinaten eingesetzt und wird außerdem $\mathrm {d} s^{2}=0$ (für die Nullgeodäte) gesetzt, so ergibt sich

${\dot {R}}^{2}=E^{2}-P^{2}-{\frac {L^{2}}{R^{2}}}\geq 0.$

Daraus ergibt sich für den minimalen Radius R_min einer Nullgeodäte

$E^{2}-P^{2}-{\frac {L^{2}}{R_{\mathrm {min} }^{2}}}=0\quad$ also $\quad R_{\mathrm {min} }={\frac {|L|}{\sqrt {E^{2}-P^{2}}}}$

und weiter

${\dot {R}}^{2}=L^{2}\left({\frac {1}{R_{\mathrm {min} }^{2}}}-{\frac {1}{R^{2}}}\right).$

Damit ist für ${\ddot {R}}$ das erste Integral ebenfalls gefunden.

Abb. 7: Auf der linken Seite sind radiale Nullgeodäten in Born-Koordinaten abgebildet. Die grüne Kurve zeigt einen auslaufenden Lichtstrahl, die rote Kurve einen einlaufenden Lichtstrahl. Die im Gegenuhrzeigersinn rotierenden Langevin-Beobachter sitzen auf dem blauen Ring mit R = R₀.
• Die Parameter für diese Kurven sind: ω = +0,2, R₀ = r₀ = 1.

Auf der rechten Seite sind Nullgeodäten in Born-Koordinaten zwischen zwei Langevin-Beobachtern auf dem Ring r = r₀ = 1 abgebildet. Nullgeodäten in Rotationsrichtung (im Gegenuhrzeigersinn – grüne Kurve) sind einwärts gebogen, Nullgeodäten gegen die Rotationsrichtung (im Uhrzeigersinn – rote Kurve) sind auswärts gebogen. Die Eigenzeit für den Langevin-Beobachter Δt₁₂, die der Lichtstrahl von L₁ nach L₂ benötigt, ist 1,311, die Eigenzeit Δt₂₁ von L₂ nach L₁ ist 1,510. Diese beiden Zeit sind nicht identisch (asymmetrisch für die Beobachter L₁ L₂), die Radardistanz (Δt₁₂ + Δt₂₁)/2 jedoch schon. Für ω → 0 gehen beide Zeiten Δt₁₂ und Δt₂₁ gegen √2 = 1,414.
• Die Parameter für diese Kurven und die nächsten sind: ω = +0,1, R₀ = r₀ = 1, Δϕ(L₁,L₂) = π/2, Δϕ(L₁,L₃) = π

In der Mitte sind Nullgeodäten zwischen gegenüberliegenden Langevin-Beobachtern L₁ und L₃ (graue Kurven) zu sehen, die sich symmetrisch um das Rotationszentrum biegen.

Die Lösung der Nullgeodäten als Kurven mit dem affinen Parameter λ ist (siehe Abb. 6)

${\begin{aligned}R&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,\lambda ,\\[1em]Z&=Z_{0}+P\,\lambda ,\\\Phi &=\Phi _{0}+\operatorname {arctan} \left({\frac {E^{2}-P^{2}}{L}}\,\lambda \right)=\\&=\Phi _{0}+\operatorname {arctan} \left({\frac {\sqrt {E^{2}-P^{2}}}{R_{\mathrm {min} }\,\operatorname {sgn} {(L)}}}\,\lambda \right).\end{aligned}}$

Die Trajektorien der Nullgeodäten, also die Spuren ihrer „Projektion“ in die räumliche Hyperebene $T=\mathrm {const.}$ sind im Minkowski-Raum mit Zylinderkoordinaten natürlich Geraden und gegeben durch

$R={\frac {R_{\mathrm {min} }}{\cos(\Phi -\Phi _{0})}}.$

Für radiale Nullgeodäten ist $R_{\mathrm {min} }=0$. Außerdem gilt mit $E=1,\,P=0$ in die Gleichungen oben eingesetzt für auslaufende radiale Nullgeodäten

$T=\lambda ,\;Z=Z_{0},\;R=\lambda ,$

$\Phi =\mathrm {const.} =\omega \,R_{0}.$

$R_{0}$ ist der Abstand des Langevin-Beobachters vom Rotationszentrum (siehe Abb. 7). Werden diese Gleichungen in Born-Koordinaten transformiert, ergibt sich für den auslaufenden Lichtstrahl

$r=r_{0}-{\frac {\phi }{\omega }}.$

In Born-Koordinaten ist diese Trajektorie keine Gerade (siehe die grüne Kurve in der Abb. 7). Wie im Abschnitt Transformation in Born-Koordinaten gezeigt, handelt es sich in Born-Koordinaten bei diesen Trajektorien streng genommen nicht um eine Projektion in eine räumliche Hyperebene, da eine solche für $t=\mathrm {const.}$ nicht definiert ist (siehe Abb. 5).

Für einlaufende radiale Nullgeodäten ergibt sich

$r={\frac {\phi }{\omega }}$

dargestellt als rote Kurve in Abb. 7.

Um einen Laserimpuls zum stationären Beobachter S bei r = 0 zu senden, muss der Langevine-Beobachter bei r = R₀ voraus zielen (für ihn bewegt sich S gegen den Uhrzeigersinn von rechts nach links). Das Gleiche gilt für den Beobachter S, der einen Laserimpuls zum Beobachter L schicken will. Für ω > 0 sind die ein- und auslaufenden Nullgeodäten unterschiedliche Kurven in der Raumzeit mit unterschiedlichen Trajektorien.

Nullgeodäten zwischen Langevin-Beobachtern auf dem Ring mit r = R₀ sind für ω > 0 ebenfalls nach innen oder nach außen gebogen. Um dies zu sehen, werden die Gleichungen für die in Rotationsrichtung laufenden Nullgeodäten in Zylinderkoordinaten in der Form

$T=R_{\mathrm {min} }\,\tan(\Phi ),$

$R={\frac {R_{\mathrm {min} }}{\cos(\Phi )}}$

geschrieben. Die Transformation in Born-Koordinaten ergibt

$t=r_{\mathrm {min} }\,\tan(\phi +\omega \,t),$

$r={\frac {r_{\mathrm {min} }}{\cos(\phi +\omega \,t)}}$

oder nach r und ϕ aufgelöst

$r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},$

$\phi =-\omega \,t+\operatorname {arctan} (t/r_{\mathrm {min} }).$

Diese Trajektorie ist für ω > 0 tatsächlich nach innen gebogen (siehe die grüne Kurve in Abb. 7). Für Nullgeodäten gegen die Rotationsrichtung (siehe die rote Kurve in Abb. 7) ergeben sich die Kurven

$r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},$

$\phi =-\omega \,t-\operatorname {arctan} (t/r_{\mathrm {min} })$

deren Trajektorien nach außen gebogen sind. Für die Langevin-Beobachter gilt, dass sie um sich Laserimpulse zu senden vorhalten müssen.

Damit sind die Betrachtungen zu Nullgeodäten abgeschlossen, denn eine Nullgeodäte ist entweder radial oder hat einen minimalen Radius r_min.

Radardistanz im Großen

Abb. 8: Hin- und rücklaufende Nullgeodäten (Laserimpulse) in Born-Koordinaten zwischen den beiden Langevin-Beobachtern A und B auf dem rotierenden Ring mit dem Radius r₀ und der Winkelgeschwindigkeit ω. Die grüne Kurve zeigt die Nullgeodäte für den entgegen der Rotationsrichtung laufenden Impuls, die rote Kurve für den in Rotationsrichtung laufenden Impuls. Die Laufzeit (Eigenzeit) von A nach B Δτ_AB ist kleiner als die Laufzeit von B nach A Δτ_BA. Die Radardistanz (Δτ_AB+Δτ_AB)/2 von B für A ist identisch mit der Radardistanz von A für B.

Für beschleunigte Beobachter gibt es selbst im einfachsten Fall des flachen Minkowski-Raumes verschiedene Möglichkeiten zur Entfernungsmessung, die sich als operational sinnvoll erweisen. Von diesen ist die Radardistanz die einfachste. Misst ein stationärer Beobachter C im Drehzentrum der Scheibe R = r = 0 die Laufzeit zu einem Langevin-Beobachter A auf einem Ring mit dem Radius $r_{0}$, so erhält er als Ergebnis $r_{0}$. Für den Langevin-Beobachter A ist die Situation anders. Er misst eine etwas kürzere Laufzeit, da seine Uhr im Vergleich zur Uhr des stationären Beobachters C um den Faktor ${\sqrt {1-\omega ^{2}r_{0}^{2}}}$ zeitdilatiert ist. Er erhält als Ergebnis seiner Messung $r_{0}{\sqrt {1-\omega ^{2}r_{0}^{2}}}$. Bereits dieser einfache Fall zeigt sich widersprüchlich. Die Beobachter A und C sind sich über ihren Abstand nicht einig. Die Radarmessung liefert kein symmetrisches Ergebnis.

Im Vergleich dazu liefert die Radarmessung zwischen zwei Langevin-Beobachtern A und B auf dem Ring mit dem Radius $r_{0}$ ein symmetrisches Ergebnis. Der Beobachter A misst den Abstand zu B gleich wie der Beobachter B den Abstand zu A (siehe Abb. 9). Die Laufzeiten zwischen A und B können mit den Gleichungen für die allgemeinen Nullgeodäten ermittelt werden. Mit dem Winkel ΔΦ zwischen A und B ergibt sich für die Laufzeit Δt_AB (in Koordinatenzeit) von A nach B

$\Delta \phi =+\omega \,\Delta t_{AB}+2\operatorname {arctan} \left(\Delta t_{AB}/{\sqrt {4r_{0}^{2}-\Delta t_{AB}^{2}}}\right)$

und für die Laufzeit Δt_BA (in Koordinatenzeit) von B nach A

$\Delta \phi =-\omega \,\Delta t_{BA}+2\operatorname {arctan} \left(\Delta t_{BA}/{\sqrt {4r_{0}^{2}-\Delta t_{BA}^{2}}}\right).$

Die beiden Laufzeiten können mit diesen nichtlinearen Gleichungen numerisch berechnet werden. Die Radardistanz unter Berücksichtigung der Zeitdilatation ist damit

$l={\sqrt {1-\omega ^{2}r^{2}}}\;{\frac {\Delta t_{AB}+\Delta t_{BA}}{2}}.$

Trotz der dargestellten Schwierigkeiten bei der Bestimmung von Radardistanzen im Großen lässt sich beispielsweise mit Märzke-Wheeler-Koordinaten für einen bestimmten Langevin-Beobachter eine Gleichzeitigkeitsfläche konstruieren, mit deren Hilfe sich große Radardistanzen messen lassen.

Radardistanz im Kleinen

Wie im Abschnitt Transformation in Born-Koordinaten gezeigt, lassen sich mit Born-Koordinaten keine „Gleichzeitigkeitsflächen“ festlegen. Jedoch ist die zeitartige Kongruenz der Langevin-Beobachter stationär und ihre Weltlinien können durch Punkte ersetzt werden. Dadurch wird ein Quotientenraum des Bereichs $0<R<1/\omega$ des Minkowskiraums gebildet. Dieser Raum ist eine dreidimensionale topologische Mannigfaltigkeit, die sich durch eine Riemannsche Metrik in eine dreidimensionale Riemannsche Mannigfaltigkeit wandeln lässt, mit der sich einfach operational Abstände finden lassen.

Ausgangspunkt ist das Linienelement in Born-Koordinaten

$\mathrm {d} s^{2}=(1-\omega ^{2}\,r^{2})\,\mathrm {d} t^{2}-2\,\omega \,r^{2}\,\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\,\mathrm {d} \phi ^{2},$

$-\infty <t,z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi .$

Wird $\mathrm {d} s^{2}=0$ gesetzt und nach $\mathrm {d} t$ aufgelöst, ergeben sich die Lichtlaufzeiten hin und zurück

$\mathrm {d} t_{+}={\frac {\omega \,r^{2}\,\mathrm {d} \phi +{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}},$

$\mathrm {d} t_{-}={\frac {\omega \,r^{2}\,\mathrm {d} \phi -{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}}.$

Und damit die lokale (infinitesimale) Radardistanz als arithmetischer Mittelwert der Lichtlaufeigenzeit

${\sqrt {1-\omega ^{2}\,r^{2}}}\;{\frac {\mathrm {d} t_{+}-\mathrm {d} t_{-}}{2}}={\sqrt {\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}}}}.$

Somit hat der Quotientenraum das Riemannsche Linienelement

$\mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}},$

$-\infty <z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi$

das dem Abstand zweier benachbarter Langevin-Beobachter mit infinitesimalem Abstand entspricht. Diese Metrik wird Langevin-Landau-Lifschitz-Metrik genannt und stellt die „Radardistanz im Kleinen“ dar. Diese Metrik wurde von Langevin eingeführt und von Lifschitz und Landau als „Radardistanz im Kleinen“ für durch beliebige stationäre zeitartige Kongruenzen gebildete Quotientenräumen von Lorentzmannigfaltigkeiten verallgemeinert.

Für den Quotientenraum der Langevin-Landau-Lifschitz-Metrik berechnet sich der Krümmungsskalar mit

${R}={\frac {-6\omega ^{2}}{(1-\omega ^{2}r^{2})^{2}}}=-6\omega ^{2}+{\mathcal {O}}(\omega ^{4}).$

Dieser ist bis Größen vierter Ordnung in $\omega$ identisch mit der konstanten negativen Krümmung des Hyperbolischen Raums mit dem Linienelement

$\mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {\sinh ^{2}({\sqrt {3}}\omega r)}{3\omega ^{2}}}\;\mathrm {d} \phi ^{2},$

$-\infty <z<\infty ,\;\;0<r<\infty ,\;\;-\pi <\phi <\pi$

und dem Krümmungsskalar

${R}=-6\omega ^{2}.$

In diesem Sinne ist die „Geometrie der rotierenden Scheibe“ tatsächlich gekrümmt und entspricht in der Näherung dem Hyperbolischen Raum, wie Theodor Kaluza bereits 1910 (ohne Beweis) vermutet hat. Wie jedoch oben gezeigt wurde, gibt es unterschiedliche Möglichkeiten Abstände auf der rotierenden Scheibe zu messen, die sehr unterschiedliche Ergebnisse liefern. Mit der Langevin-Landau-Lifschitz-Metrik lässt sich ebenso wie mit der Radardistanz im Großen, der radiale Abstand eines Langevin-Beobachters am Ring mit Radius $r_{0}$ vom Rotationszentrum ermitteln. Dazu wird das entsprechende Linienelement für die oben angegebene Nullgeodäte integriert.

$\mathrm {d} r={\frac {\mathrm {d} \phi }{\omega }},\quad \mathrm {d} z=0$

in das Linienelement eingesetzt ergibt

$\int _{0}^{\Delta }\mathrm {d} \sigma =\int \limits _{0}^{r_{0}}{\left(1+{\frac {\omega ^{2}r^{2}}{1-\omega ^{2}r^{2}}}\right)^{\frac {1}{2}}}\,\mathrm {d} r$

und weiter

$\Delta =\int _{0}^{r_{0}}{\frac {\mathrm {d} r}{\sqrt {1-\omega ^{2}\,r^{2}}}}={\frac {\arcsin(\omega r_{0})}{\omega }}=r_{0}+{\frac {\omega ^{2}\,r_{0}^{3}}{6}}+{\mathcal {O}}(r_{0}^{5}).$

Dieser Abstand ist größer als $r_{0}$, während die „Radardistanz im Großen“ gleich oder kleiner als $r_{0}$ ist.

Da die zugrunde liegende Langevin-Landau-Lifschitz-Metrik eine Riemann-Metrik ist, ist dieser Abstand im Gegensatz zur „radialen Radardistanz im Großen“ symmetrisch. Der Riemannsche Krümmungstensor der (gekrümmten) Langevin-Landau-Lifschitz-Metrik ist operational signifikant. Wie Nathan Rosen festgestellt hat, stimmen für benachbarte Langevin-Beobachter die gemessenen lokalen (infinitesimalen) Abständen mit jenen überein, die von einem inertialen Beobachter gemessen werden, der sich in einem bestimmten Augenblick parallel und synchron zu ihnen bewegt.

Siehe auch

• Geschichte der speziellen Relativitätstheorie – Starre Körper und Realität der Längenkontraktion
• Paul Ehrenfest
• Nichteuklidische Geometrie
• Laserkreisel
• Tests der speziellen Relativitätstheorie

Quellen

Standardwerke

1. Grøn, Ø.: Relativistic description of a rotating disk. In: Amer. J. Phys. 43. Jahrgang, Nr. 10, 1975, S. 869–876, doi:10.1119/1.9969, bibcode:1975AmJPh..43..869G. 
2. Landau, L. D., Lifschitz, E. M.: The Classical Theory of Fields (4th ed.). Butterworth-Heinemann, London 1980, ISBN 0-7506-2768-9. 
   • Für die Beschreibung der Langevin-Landau-Litschitz-Metrik als Quotient einer Lorentzschen Mannigfaltigkeit durch eine stationäre Kongruenz siehe Abschnitt 84 und das Beispiel für die Anwendung eines Langevin-Beobachters am Ende des Abschnitts 89.

Weblinks

• The Rigid Rotating Disk in Relativity, by Michael Weiss (1995), from the sci.physics FAQ.
• arxiv:gr-qc/9904078: Hrvoje Nikolic: Relativistic contraction and related effects in noninertial frames.
• arxiv:gr-qc/0207104: Guido Rizzi, Matteo Luca Ruggiero: Space geometry of rotating platforms: an operational approach.
• arxiv:gr-qc/0403111: Olaf Wucknitz: Sagnac effect, twin paradox and space-time topology – Time and length in rotating systems and closed Minkowski space-times.