Diskussion:Areasekans hyperbolicus und Areakosekans hyperbolicus
Zusammenführung Areasekans Hyperbolicus mit Areakosekans Hyperbolicus
[Quelltext bearbeiten]Versionsliste von Areakosekans Hyperbolicus
[Quelltext bearbeiten]- 17:48, 21. Mai 2006 König Alfons der Viertelvorzwölfte (?Eigenschaften)
- 02:37, 7. Jan 2006 Bsmuc64
- 17:00, 4. Jan 2006 Fredstober K (?Ableitung)
- 10:23, 4. Jan 2006 Exxu K (?Integral - Formelumstellung zwecks eindeutigerer Lesbarkeit)
- 00:39, 4. Jan 2006 Fredstober K (?Reihenentwicklung - Abk. vereinheitlicht)
- 00:21, 4. Jan 2006 Exxu K (Erg.)
- 22:19, 3. Jan 2006 Fredstober (?Reihenentwicklung)
- 21:58, 3. Jan 2006 Fredstober K (?Definition)
- 20:14, 3. Jan 2006 Fredstober (Ich greife mal das Vorhaben von Benutzer:Bsmuc64 auf.)
- 19:01, 3. Jan 2006 Thomas S. (LA+)
- 02:24, 3. Jan 2006 Fredstober (+Bild)
- 22:07, 2. Jan 2006 Bsmuc64 K (Vermeidung von kaputten Redirects)
Definitionen
[Quelltext bearbeiten]Die Formel des ArCscH im Abschnitt "Definitionen" funktioniert nur für positive x. Formeln, die funktionieren, habe ich im neuen Abschnitt "Umrechnung und Beziehungen zu anderen trigonometrischen Funktionen" ergänzt (Konsistent zu diesem Artikel). (nicht signierter Beitrag von Asfdlol (Diskussion | Beiträge) 10:42, 12. Sep. 2014 (CEST))
Bilder
[Quelltext bearbeiten]Warum werden im Artikel Rastergrafiken verwendet, wenn Vektorgrafiken verfügbar ist?
-
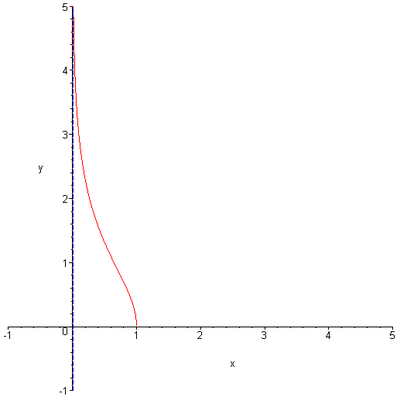
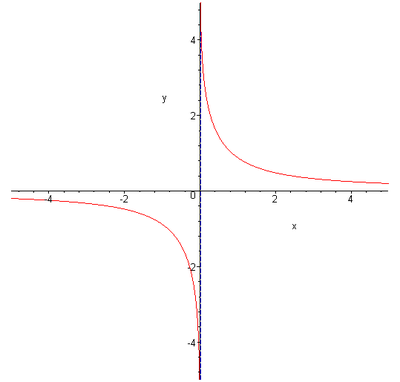
Rastergrafik im Artikel
-
Vektorgrafik
-
Rastergrafik im Artikel
-
Vektorgrafik
@Asfdlol:@Bsmuc64: Gibt es Änderungswünsche an der Vektorgrafik? --Martin Thoma 07:11, 9. Nov. 2015 (CET)
Fehler in der Definition des Areakosinus hyperbolicus
[Quelltext bearbeiten]Die Funktionsgleichung $\operatorname{arcsch}(x) = \ln \left( \frac{1 + \sqrt{1+x^2}} {x} \right)$ ist nur für $x>0$ definiert. Da der Kosekans hyperbolicus allerdings für $x\in\RR\backslash\{0\}$ bijektiv ist, ist $\operatorname{arcsch}(x)$ durchaus für $x\in\RR\backslash\{0}$ definiert, allerdings stückweise: $\operatorname{arcsch}(x) = \begin{cases}\ln\left(\frac{1+\sqrt{1+x^2}}x\right)&,\text{für }x>0\\\ln\left(\frac{1-\sqrt{1+x^2}}x\right)&,\text{für }x<0\end{cases} $ --Matheholikerin (Diskussion) 11:36, 1. Nov. 2023 (CET)