Kollabierender Zirkel
Der kollabierende Zirkel,[1] auch euklidischer Zirkel[2] oder Klappzirkel[3] genannt, ist ein Zirkel, der beim Hochheben vom Blatt zuschnappt, so dass er sich nicht unmittelbar zum Übertragen von Strecken eignet. Dabei handelt es sich um eine eher theoretische Überlegung, denn die meisten Zirkel kollabieren nicht.
Euklid verwendet in seiner Geometrie kollabierende Zirkel. In Proposition 2 von Buch I der Elemente beweist er, wie man mit einem solchen Zirkel und einem Lineal eine beliebige Strecke übertragen kann.[3]
Auch ohne Lineal kann mit einem kollabierenden Zirkel ein Kreis mit gegebenem Radius an einen beliebigen anderen Ort übertragen werden.
Problemstellung und Begriffsklärung[Bearbeiten | Quelltext bearbeiten]
Bei Konstruktionen mit Zirkel und Lineal wird meist ein nicht-kollabierender Zirkel verwendet. In den ursprünglichen Konstruktionsproblemen des Euklid wurde jedoch von einem kollabierenden Zirkel ausgegangen, dessen Radius beim Hochheben vom Blatt nicht festgehalten werden kann, um einen weiteren Kreis mit diesem Radius zu zeichnen.
Laut Euklid existieren zu zwei Punkten A und B immer eine (mit einem Lineal konstruierbare) Gerade, die durch beide Punkte verläuft, sowie zwei Kreise, einer um A und einer um B, mit dem Radius der Strecke von A bis B.
Damit erhält man also beinahe alle möglichen Konstruktionen, die man mit einem Zirkel und einem Lineal machen kann, bis auf das Abgreifen einer Strecke AB mit einem Zirkel und das Ziehen eines Kreises mit diesem Radius um einen dritten Punkt C.
Ein kollabierender Zirkel ist also ein Zirkel, mit dem man einen Kreis ziehen kann. Allerdings bricht nach dem Zeichnen des Kreises der eingestellte Radius zusammen: Der Zirkel schnappt zusammen, so dass man den Zirkel nicht auf einen anderen Punkt setzen und einen Kreis mit demselben Radius ziehen kann – es sei denn, es existiert bereits ein Punkt, der vom neuen Punkt schon diesen Abstand hat.
Tatsächlich resultiert daraus jedoch, dass durch weitere Schritte mit einem kollabierenden Zirkel und einem Lineal auch solche Kreise konstruiert werden können, die mit dem Radius als Abstand zweier Punkte um einen dritten Punkt gezogen werden können. Beweis siehe unten.
Mathematische Erläuterung für Konstruktionen mit Zirkel und Lineal[Bearbeiten | Quelltext bearbeiten]
Sei eine Menge von Punkten im , die Menge aller Geraden im , die durch mindestens zwei Punkte aus verlaufen, die Menge aller Kreise, deren Mittelpunkte die Punkte aus und deren Radien gleich den Abständen zweier Punkte aus sind.
Dann ist die Menge aller Punkte, die aus durch Konstruktionen mit Zirkel und Lineal konstruiert werden können mithilfe folgender Operationen:
- Schnitt zweier verschiedener Geraden aus
- Schnitt einer Geraden aus mit einem Kreis aus
- Schnitt zweier verschiedener Kreise aus
Für macht es keinen Unterschied, ob mit einem kollabierenden oder einem nicht-kollabierenden Zirkel gearbeitet wird, denn alle Punkte aus , die mithilfe eines nicht-kollabierenden Zirkels konstruiert werden können, können auch mit einem kollabierenden Zirkel konstruiert werden. Beweis siehe Konstruktion unten.
Allerdings: Sei nun die Menge aller Punkte, die aus M durch Konstruktionen mit einem kollabierenden Zirkel und Lineal und die Menge aller Punkte, die aus M durch Konstruktionen mit einem nicht-kollabierenden Zirkel und Lineal in nur einem Schritt konstruiert werden können.
Dann gilt: , denn schon für eine dreielementige Menge von Punkten A, B, C ist der Schnittpunkt einer Geraden durch A und B mit einem Kreis mit Radius um C zwar in , jedoch nicht in . Die Konstruktion dieses Kreises um C erfordert mit einem kollabierenden Zirkel einige Schritte mehr (siehe unten).
Konstruktion eines Kreises um einen Punkt mit Abstand zweier anderer Punkte als Radius mit einem kollabierenden Zirkel[Bearbeiten | Quelltext bearbeiten]
Um zu zeigen, dass mit einem kollabierenden Zirkel und einem Lineal dieselben Punkte konstruierbar sind wie mit einem nicht-kollabierenden Zirkel und einem Lineal, genügt es zu zeigen, dass mit kollabierendem Zirkel und Lineal die Konstruktion eines Kreises um einen Punkt mit Abstand zweier anderer Punkte als Radius möglich ist. Schnitte aus einem solchen Kreis mit einer Geraden oder mit einem anderen (evtl. ebensolchen) Kreis sind dann ohne Weiteres möglich, da ja schon beide Kreise (bzw. der Kreis und die Gerade) konstruiert werden können, also dementsprechend auch deren Schnitte.
Beweis[Bearbeiten | Quelltext bearbeiten]
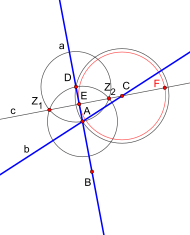
(1) Gegeben seien drei Punkte A, B, C. In der Zeichnung sind die Geraden durch A und B sowie durch A und C bereits eingezeichnet. Die Gerade durch B und C wird nicht benötigt.
Ziel ist es, einen Kreis um C zu konstruieren, der als Radius die Streckenlänge hat, um damit einen Schnittpunkt mit der Geraden zu erzeugen.
Dafür müssen zwei Parallelen gebildet werden, je eine zu jeder der beiden bereits vorhandenen Geraden. Die erste Parallele (zu ) soll dabei durch Punkt C gehen, und die zweite Parallele (zu ) soll durch Punkt B gehen.
(2) Zur Konstruktion der ersten dieser Parallelen wird um den Punkt C ein Kreis mit Radius gezogen. Dieser schneidet die Gerade in A und einem weiteren Punkt D. (Wenn senkrecht auf steht, ist natürlich . In diesem Fall kann der nächste Schritt ausgelassen und direkt A als der in diesem Schritt zu bestimmende Punkt E verwendet werden.)
(3) Nun werden um A und um D jeweils ein Kreis mit Radius gezogen und die Schnittpunkte dieser beiden Kreise (hier Z1 und Z2) verbunden zur Geraden . Die Gerade ist ein Lot von C auf , d. h. eine zu senkrechte Gerade durch C. Der Lotfußpunkt, d. h. der Schnittpunkt von mit , wird als E bezeichnet.
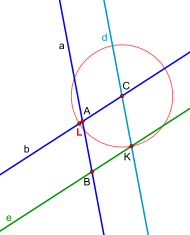
(4) Es folgt das Bestimmen des Punktes F auf dieser Senkrechten im gleichen Abstand wie E von C, indem um C ein Kreis mit Radius gezogen wird.
(5) Mithilfe von E und F können nun zwei Kreise mit Radius gezeichnet werden, die sich in zwei Punkten (hier G und H) schneiden. Diese beiden Punkte definieren eine Senkrechte zur Senkrechten () zu (also eine Parallele zu ), die durch Punkt C verläuft. Diese Parallele wird genannt. Somit ist die erste Parallele konstruiert. Auf die gleiche Weise kann die Parallele zu konstruiert werden. Man erhält damit ein Parallelogramm und den Schnittpunkt K der beiden Parallelen und .
(6) Für eine bessere Übersichtlichkeit, sind die beiden Konstruktionen der Parallelen auf zwei Bilder aufgeteilt.
(7) Die Strecke ist also offensichtlich so lang wie .
(8) Nun muss nur noch ein Kreis mit Radius um C gezogen werden. Dieser schneidet . Schnittpunkt L ist der gesuchte Punkt.
Anmerkung[Bearbeiten | Quelltext bearbeiten]
Der Beweis setzt voraus, dass C nicht auf liegt. In einem solchen Fall kann mit der beschriebenen Methode ein Kreis mit dem Radius um einen beliebigen Punkt P gezeichnet werden, der nicht auf liegt (d. h., P wird statt C in obiger Konstruktion verwendet). Während der Konstruktion entsteht dann auch eine Gerade (analog zu in obiger Konstruktion), die durch P geht und zu parallel ist. Der konstruierte Kreis schneidet in zwei Punkten Q und R (analog zu K in obiger Konstruktion), wobei offenbar gilt, dass .
Damit kann die Konstruktion ein zweites Mal durchgeführt werden, wobei die Länge einer dieser beiden Strecken als Radius für den Kreis um C verwendet wird (d. h., nun werden P und Q als A und B in obiger Konstruktion angewandt). Da und parallel sind und da C auf liegt, P aber nicht, liegt auch C nicht auf , also gelingt die Konstruktion jetzt. Außerdem kann dadurch die Konstruktion einer Parallelen zu in der anschließenden Konstruktion offenbar übersprungen werden.
Anwendung[Bearbeiten | Quelltext bearbeiten]
Parallele zu einer Geraden durch einen vorgegebenen Punkt[Bearbeiten | Quelltext bearbeiten]

Die nebenstehende Abbildung zeigt eine konstruktive Lösung, die neben dem gegebenen Punkt und der gegebenen Geraden nur drei Kreise mit gleichem Radius und die Gerade für die Lösung benötigt. Im Verlauf der Konstruktion werden für das Ziehen eines Kreises stets zwei Punkte genutzt. Der Abstand der beiden Punkte ist gleich dem Kreisradius, aufgrund dessen kann ein kollabierender Zirkel verwendet werden.
- Zeichne den ersten Kreis um den auf der Geraden gewählten Punkt durch den Punkt . Er schneidet die Gerade im Punkt
- Zeichne den zweiten Kreis um den Punkt durch den Punkt
- Zeichne den dritten Kreis um den Punkt durch den Punkt Er schneidet den Kreis um in
- Die Gerade durch und ist die gesuchte Parallele.
Übertragung eines Kreises ohne Lineal[Bearbeiten | Quelltext bearbeiten]

Gegeben sind die Punkte , und . Alleine mit dem kollabierenden Zirkel soll ein Kreis um mit dem Radius konstruiert werden.
- Zeichne einen Kreis um , der enthält und umgekehrt (blaue Kreise). Die Kreise schneiden sich in den Punkten und .
- Zeichne Kreise durch um und (rote Kreise). Benenne den zweiten Schnittpunkt der Kreise .
- Zeichne einen Kreis (grüner Kreis) um , der enthält. Dies ist der gewünschte Kreis.[4][5]
Mit als Spiegelachse sind die Punkte und eine Abbildung von und und .
Literatur[Bearbeiten | Quelltext bearbeiten]
- C. Bessenrodt: Algebra I, Wintersemester 2003/2004 - Punkt 1.1 - Vorlesungsskript (PDF; 1,0 MB)
- Robin Hartshorne: Euclid and Beyond 1. Euklid's Geometry Springer-Verlag New York, Inc. in 2000; 2 Ruler and Compass Constructions, Seite 18.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Knut Smoczyk: Geometrie für das Lehramt, Norderstedt: Books on Demand, 2019, Seite 221, 7.1. Euklidische Werkzeuge; (Online-Kopie (BoD)) ISBN 978-3-7481-6616-0; abgerufen am 25. März 2019.
- ↑ Heinz Lüneburg: Von Zahlen und Größen. Band 2. Birkhäuser, ISBN 978-3-7643-8778-5, Seite 336.
- ↑ a b William Dunham: Mathematik von A–Z: Eine alphabetische Tour durch vier Jahrtausende, Springer Basel AG, Griechische Geometrie, Seite 103 ff.; abgerufen am 30. Dezember 2018.
- ↑ Howard Eves: A survey of Geometry (Vol. I). Allyn Bacon, 1963, S. 185.
- ↑ James R. Smart: Modern Geometries. 5. Auflage. Brooks/Cole, 1997, ISBN 0-534-35188-3, S. 212.