Lösen von Ungleichungen
Beim Lösen von Ungleichungen über den reellen Zahlen versucht man, eine unübersichtliche Ungleichung so weit zu vereinfachen, dass sich einfache Aussagen etwa der Form x>5 bilden, die unmittelbar zu verstehen sind oder die sich an der Zahlengeraden veranschaulichen lassen. Im Prinzip gelten hier die gleichen Grundregeln wie für das Lösen von Gleichungen. Allerdings erfordert die Asymmetrie der Vergleichszeichen darüber hinaus ein besonderes Augenmerk auf die Vorzeichen der Umformungen.
Grundregeln[Bearbeiten | Quelltext bearbeiten]
Ähnlich wie beim Lösen von Gleichungen werden Ungleichungen durch Äquivalenzumformungen gelöst. Das heißt, es sind eine Reihe von Aktionen erlaubt – vorausgesetzt, sie werden auf beiden Seiten gleich ausgeführt. Im Folgenden wird nur das Kleiner-gleich-Zeichen betrachtet; analoge Aussagen gelten aber, wenn das Kleiner-gleich-Zeichen durch eines der anderen Symbole oder ersetzt wird.
Ohne Einschränkung sind Addition und die Subtraktion des gleichen Ausdrucks auf beiden Seiten Äquivalenzumformungen. Es gilt also für zwei reellwertige Terme und beliebige
- sowie
- .
Bei der Multiplikation mit dem gleichen Ausdruck und bei der Division durch den gleichen Ausdruck ist auf das Vorzeichen zu achten: Für zwei reellwertige Terme und mit gilt
- sowie
- .
Für dreht sich hingegen die Ordnungsrelation um:
- sowie
- .
Der Fall ist offensichtlich keine Äquivalenzumformung.
Generell gilt für eine bijektive streng monoton steigende Funktion
- ,
für eine bijektive streng monoton fallende Funktion dreht sich hingegen die Ordnungsrelation um:
- .
Die oben beschriebenen Fälle der Addition, Subtraktion, Multiplikation und Division sind Spezialfälle dieser allgemeinen Regel, so entspricht beispielsweise der Multiplikation mit die Anwendung der Funktion , die für bijektiv und streng monoton steigend, für bijektiv und streng monoton fallend, für weder bijektiv noch streng monoton ist.
Oft möchte man Funktionen anwenden, die nicht auf ganz , sondern nur auf einer Teilmenge streng monoton sind. Das ist möglich, wenn sichergestellt ist, dass die Terme in dieser Teilmenge liegen. Beispielsweise gilt für eine bijektive streng monoton wachsende Funktion
- ,
für eine bijektive streng monoton fallende Funktion
- .
In diesem Fall muss entweder gezeigt werden, dass tatsächlich immer gelten muss, oder eine Fallunterscheidung getroffen werden, in dem man zunächst den Fall untersucht und dann die Fälle und getrennt behandelt.
Wichtigster Spezialfall ist das Potenzieren beider Seiten mit dem gleichen Exponenten:
- für ,
- für .
entspricht dem Ziehen der Quadratwurzel:
- ,
dem Bilden des Kehrwertes:
- .
Arten von Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Lineare Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Einzelne lineare Ungleichungen können durch Addition, Subtraktion und Multiplikation mit Konstanten ähnlich wie lineare Gleichungen gelöst werden. Ein wichtiger Ansatz für Systeme linearer Ungleichungen in mehreren Variablen bieten Pivotverfahren und, ganz allgemein, Verfahren der linearen Optimierung.
Quadratische Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Bei quadratischen Ungleichungen zerfällt der Lösungsbereich üblicherweise in drei Abschnitte, die sich aus der der Ungleichung entsprechenden quadratischen Gleichung ergeben. Diese sind in der unter Graphische Verfahren gezeigten Abbildung die Abschnitte blau – rot – blau. Als Lösungen kommen nun entweder alle blau markierten oder alle rot markierten Werte der x-Achse infrage.
Lösung mit Quadratischer Ergänzung[Bearbeiten | Quelltext bearbeiten]
Ein Verfahren zur Lösung basiert im Wesentlichen auf der Quadratischen Ergänzung. Als Beispiel soll die Ungleichung x² − 0,5·x − 0,5 > 0 gelöst werden, die unten im Bild dargestellt ist.
x² − 0,5·x − 0,5 > 0 | + 0,5 x² − 0,5·x > 0,5 | + (0,5 : 2)² (das Quadrat der Hälfte des Betrags des linearen Gliedes addieren) x² − 0,5·x + 0,25² > 0,5625 | ausklammern (x − 0,25)² > 0,75² | Wurzel ziehen
Hier darf man nicht einfach „das Quadrat wegkürzen“. Da aber , darf auf beiden Seiten die Wurzel gezogen werden. Dabei ist zu beachten, dass gilt. Wir haben also zwei Fälle zu unterscheiden:
Fall 1: . Dann ist die Ungleichung zu lösen, also gilt , wobei in diesem Fall die Voraussetzung ebenfalls erfüllt ist.
Fall 2: . Dann ist die Ungleichung zu lösen, also gilt , wobei auch in diesem Fall die Voraussetzung erfüllt ist.
Diese beiden Aussagen haben keinen Überschneidungsbereich. Dann sind, wie man durch Ausprobieren leicht bestätigen wird, alle Zahlen, die entweder kleiner als −0,5 oder größer als +1 sind, Lösungen der Ungleichung.
Hätte man dagegen die Ungleichung x² − 0,5·x − 0,5 < 0 zu lösen gehabt, wären die Lösungsaussagen x > −0,5 und x < +1. Alle Zahlen zwischen −0,5 und +1 erfüllen beide Bedingungen und wären somit Lösungen.
Umformung auf Produkt[Bearbeiten | Quelltext bearbeiten]
Das Lösen mittels quadratischer Ergänzung erfordert mehrere Fallunterscheidungen, die unübersichtlich werden können. Ein anderes Lösungsverfahren für quadratische Ungleichungen besteht darin, die Ungleichung direkt auf ein Produkt der Art , , oder zu bringen. Als Beispiel soll ebenfalls die unten im Bild dargestellte Ungleichung gelöst werden.
Die der Ungleichung entsprechende quadratische Gleichung
hat die Lösungen und , es gilt also
und die Ungleichung ist äquivalent zu
- .
Betrachtet man nun die durch die beiden Lösungen der quadratischen Gleichung unterteilten Abschnitte der Zahlengeraden, so stellt man fest, dass für beide Faktoren negativ und das Produkt daher positiv ist sowie für beide Faktoren positiv und das Produkt daher ebenfalls positiv ist. Das ist im Bild der blaue Bereich. Im dazwischenliegenden Abschnitt ist und , das Produkt also nicht positiv. Das ist der rot markierte Bereich.
Besitzt die zur Ungleichung gehörige quadratische Gleichung keine reelle Lösung, gilt also , so gilt für alle x die Beziehung ; die Ungleichung hat also entweder gar keine Lösung oder ist für alle reellen Zahlen erfüllt.
Ungleichungen höherer Ordnung[Bearbeiten | Quelltext bearbeiten]
Bei Ungleichungen ab der Ordnung 3 ist üblicherweise nur mehr die Umwandlung auf eine Ungleichung für ein Produkt praktikabel, beispielsweise indem eine Ungleichung der Ordnung 3 auf die Form für reelle oder für ein Paar komplexer Nullstellen gebracht wird. Diese Faktorisierung ist nach dem Fundamentalsatz der Algebra für Ungleichungen beliebig hoher Ordnung möglich. Die analytische Berechnung der Nullstellen ist aber nicht immer möglich, sodass dafür meist ein numerisches Verfahren wie beispielsweise Bisektion herangezogen werden muss. Eine graphische Lösung kann bei der Suche nach geeigneten Startwerten hilfreich sein.
Bruchungleichungen[Bearbeiten | Quelltext bearbeiten]
Umformung auf Ungleichungen zwischen Polynomen[Bearbeiten | Quelltext bearbeiten]
Für das Lösen von Bruchungleichungen ergeben sich neue Aspekte nur, wenn die gesuchte Größe x auch in mindestens einem der Nenner erscheint. Durch beidseitiges Multiplizieren der Gleichung mit den Nennern und anschließendes Ausmultiplizieren wird die Bruchungleichung in eine Ungleichung aus zwei Polynomen überführt.
Beim Multiplizieren mit den Nennern ist vorher zu bestimmen, für welche Werte von x sie einen negativen Wert annehmen, da sich dann ja durch die Multiplikation das Vergleichszeichen umkehrt. Gibt es einen Bereich von x, in dem beide Nenner negativ sind, so wird das Vergleichszeichen zweimal umkehrt, was sich gegenseitig aufhebt. Diese Vorabklärung wird als Fallunterscheidung bezeichnet.
Als Beispiel soll die Ungleichung
betrachtet werden. Wie leicht ersichtlich ist, wird jeweils ein Nenner gleich Null, wenn entweder x=−0,2 oder x=−0,6. Für diese Werte von x ist die Ungleichung nicht definiert (Division durch null). Ist dagegen x kleiner als −0,6 (x<−0,6), so sind beide Nenner negativ; für x>−0,2 sind beide positiv. Dann findet keine Umkehr des Vergleichszeichens statt und es ergibt sich durch Multiplikation der Ungleichung mit den Nennern:
(x−1,6)·(x+0,6) < (0,2−x)·(x+0,2).
Sonst (x liegt zwischen −0,6 und −0,2) wird nur der linke Nenner negativ. In diesem Fall ergibt sich aus der Multiplikation und nachfolgenden Äquivalenzumformungen:
| (x−1,6)·(x+0,6) | > (0,2−x)·(x+0,2) | ausmultiplizieren! | |
| x²−1x−0,96 | > 0,04 − x² | +x² −0,04 | |
| 2x²−1x−1 | > 0 | ÷2 | |
| x²−0,5x−0,5 | > 0 |
Dies ist die quadratische Ungleichung, die bereits zuvor gelöst wurde. Ihre Lösung wäre der blaue Bereich der Abbildung. Da diese Rechnung allerdings nur für den Bereich zwischen −0,6 und −0,2 gilt (s. o.), bleiben vom blauen Bereich nur Werte zwischen −0,6 und −0,5 übrig.
Zuletzt müssen wir noch die Fälle x<−0,6 und x>−0,2, für die sich das Vergleichszeichen nicht umkehrt. Lösung der erzeugten quadratischen Ungleichung wäre dann der rote Bereich der Abbildung. Da diese Rechnung allerdings nicht für den Bereich zwischen −0,6 und −0,2 gilt, ergibt sich als Lösungsbereich der Ungleichung nur die Werte zwischen −0,2 und +1.
Fazit: Die Ungleichung ist erfüllt für −0,6<x<−0,5 und für −0,2<x<+1.
Umformung auf Produkt[Bearbeiten | Quelltext bearbeiten]
Ein anderes Verfahren zum Lösen von Bruchungleichungen besteht ebenfalls darin, die Bruchungleichung auf eine Aussage über das Vorzeichen von Produkten bzw. Quotienten umzuformen. Der Vorteil dieses Verfahrens besteht darin, dass weniger Fallunterscheidungen zu treffen sind.
Als Beispiel soll ebenfalls die Ungleichung
betrachtet werden. Statt mit dem Nenner zu multiplizieren werden alle Terme auf eine Seite gebracht; diese Umformung benötigt nur Subtraktion und daher keine Fallunterscheidung nach Vorzeichen:
Anschließend werden die Brüche auf gemeinsamen Nenner gebracht, wobei der Nenner nicht ausmultipliziert werden soll, da er später in Produktdarstellung benötigt wird:
Danach wird der Zähler ausmultipliziert und zusammengefasst
Als Nächstes wird der Zähler nach dem Fundamentalsatz der Algebra in lineare und irreduzible quadratische Terme faktorisiert; im konkreten Beispiel ist die bereits oben gelöste quadratische Gleichung zu lösen, man erhält also
Zur Bestimmung der Lösungsmenge reicht es, lediglich die Vorzeichen der jeweiligen Faktoren zu betrachten, da diese Vorzeichen gemeinsam das Vorzeichen des Produkts bestimmen. Dazu wird die Zahlengerade in einzelne Abschnitte geteilt, die jeweils durch die Nullstellen der Faktoren begrenzt werden; in jedem dieser Abschnitte sind die Vorzeichen der Faktoren konstant.
| Vorzeichen der Faktoren | Vorzeichen des Produkts | <0 | |
|---|---|---|---|
| nein | |||
| undefiniert | nein | ||
| ja | |||
| nein | |||
| nein | |||
| undefiniert | nein | ||
| ja | |||
| nein | |||
| nein |
Fazit: Die Ungleichung ist erfüllt für −0,6 < x < −0,5 und für −0,2 < x < +1.
Die systematische Nutzung und Darstellung dieses Verfahrens führt zur Vorzeichentabelle.
Betragsungleichungen[Bearbeiten | Quelltext bearbeiten]
Betragsungleichungen sind Ungleichungen, in denen mindestens ein Betrag enthalten ist. Sie können, ebenso wie Betragsgleichungen, durch Fallunterscheidung,[1] im Ausnahmefall (!) (s. u.) auch durch Quadrieren gelöst werden. Im Folgenden wird zunächst ein Zahlenbeispiel der Lösung einer einfachen Betragsungleichung vorgeführt:
Gegeben sei die Ungleichung
- .
Mit Hilfe einer Fallunterscheidung erhält man die Fälle
- und
- .
Die Lösungsmenge der Ungleichung als ganzer ist damit die Vereinigungsmenge der in diesem Fall unmittelbar aneinander grenzenden Teil-Lösungsmengen, d. h. .
Obige Ungleichung könnte man allerdings ausnahmsweise (!) auch durch Quadrieren lösen, was in diesem Fall über
zwar zum selben Ergebnis führen würde, jedoch den Nachteil hätte, dass durch das Quadrieren die Ungleichung verkompliziert und damit der Lösungsweg länger würde, vor allem aber das Vorzeichen der rechten Ungleichungsseite verloren ginge und damit bspw. die beiden Ungleichungen und dieselbe Lösungsmenge besäßen.
Nachstehendes Beispiel einer etwas schwierigeren Betragsungleichung illustriert den Fall, dass beide Teil-Lösungsmengen sich nicht zu einem zusammenhängenden Intervall vereinigen lassen:
Gegeben sei die Ungleichung
- .
Mit Hilfe der Fallunterscheidung erhält man nun die Fälle
- und
- .
Die Lösungsmenge der Ungleichung als ganzer ist damit hier wieder die Vereinigungsmenge der – in diesem Fall allerdings nicht aneinander grenzenden – beiden Teil-Lösungsmengen, d. h. .
Graphische Verfahren[Bearbeiten | Quelltext bearbeiten]
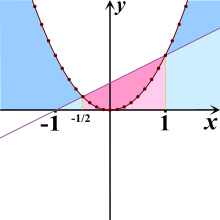
Graphische Verfahren können im Rahmen der Zeichengenauigkeit Anhaltspunkte über Anzahl und Lage der Lösungen geben.
Liegt die Ungleichung in einer der Normalform von Gleichungen entsprechenden Form vor, lässt sich die linke Seite als Funktion auffassen, deren Graph nach einer Wertetabelle mit hinreichender Genauigkeit zu zeichnen ist. Die Bereiche links oder rechts der Nullstellen (d. h. Schnittpunkte mit der x-Achse) stellen dann die Lösungsmengen graphisch dar.
Andernfalls sind die Funktionen, die der rechten und der linken Seite der Ungleichung entsprechen, zusammen in ein Achsenkreuz zu zeichnen. Die x-Werte der Schnittpunkte geben die Grenzen der Lösungsbereiche an. Quadratische Ungleichungen der rechten Seite hervorgehenden Geraden zum Schnitt bringen. Dies ist rechts exemplarisch für die Ungleichung x²<0,5x+0,5 (roter Bereich) bzw. x²>0,5x+0,5 (blauer Bereich)gezeigt.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- E. Cramer, J. Neslehova: Vorkurs Mathematik: Arbeitsbuch zum Studienbeginn in den Wirtschafts- und Sozialwissenschaften. Springer Berlin Heidelberg New York, 2006, S. 302, ISBN 3-540-26186-9.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Franz Embacher; Betragsgleichungen und die Methode der Fallunterscheidungen; Universität Wien 2014, abgerufen am 19. Juni 2016.



























































































![{\displaystyle L=\left]-6;-1\right[\cup \left[-1;4\right[=\left]-6;4\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec2b607229dca8ad1e0cdd2d4abadc5d98b2ca45)






![{\displaystyle L=\left]-\infty ;{\tfrac {-1}{5}}\right[\cup \left[{\tfrac {5}{3}};+\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d5df08e36cfedc081f6b045145263fba0eb5a89)