Äquidistante

Eine Äquidistante ist in der Geometrie eine Linie, die in einem konstanten Abstand um eine Bezugslinie herumläuft.

Parabel mit Evolvente als Beispiel

Die gestrichelte rote Linie ist eine (innenliegende) Äquidistante zu der Parabel (rote Volllinie), die auch als Evolvente bezeichnet wird. Schwarz ist die gemeinsame Evolute (Ortskurve aller Krümmungsradienmittelpunkte) eingezeichnet.

Anders ausgedrückt: Ausgangskurve und die zugeordneten Äquidistanten haben immer gemeinsame Krümmungsmittelpunkte. Der Abstand ergibt sich aus der Differenz der Krümmungsradien.

Die Evolute ergibt sich (in diesem Beispiel) aus $y \,= \, \frac{1}{2}+3 \cdot \sqrt[3]{\, \frac{x^2}{16}}$

Hüllkurve

Ist eine Kurve eine differenzierbare Untermannigfaltigkeit des R², so lässt sich für hinreichend kleines d die Äquidistante mit Abstand d von der Kurve als Enveloppe der Schar aller Kreise mit Radius d und Mittelpunkt auf der Kurve darstellen.

Parabel mit Hüllkurve einer Kreisschar als Beispiel

Schwarz: Funktionsgraph von y = x².
Rot: Jeweils eine innenliegende und eine aussenliegende Äquidistante mit Abstand 0.25 vom Funktionengraphen.
Violett: Kreise mit Mittelpunkt auf dem Funktionsgraphen und Radius 0.25. Die Äquidistante ist die Enveloppe der Schar aller solcher Kreise.
Hellblau: Strecke in Richtung des Normalenfeldes des Funktionsgraphen, die Endpunkte haben den Abstand 0.25 vom Funktionsgraphen, die Menge aller dieser Endpunkte bildet die Äquidistante.
Braun: Tangentenschar an die untere Äquidistante.

Verallgemeinerung auf Kurven und Flächen im Rⁿ

Im Folgenden ist dargestellt, wie man die Idee aus den vorhergehenden zwei Abschnitten verallgemeinern kann, um die Äquidistante für glatte Kurven und Flächen im $\mathbb{R}^n$ zu bestimmen, die sich als (reguläre) Nullstellenmenge einer Funktion f darstellen lassen.

Die Funktion $f:\mathbb{R}^n\rightarrow\mathbb{R}^r$ sei stetig differenzierbar und habe einen reguläre Nullstellenmenge (diese ist dann eine n − r-dimensionale Untermannigfaltigkeit des Rⁿ). Für hinreichend kleines d > 0 ist die Äquidistante A mit Abstand d von der Nullstellenmenge f ^{− 1}(0) von  f die Enveloppe der Sphärenschar $\big(S_d(\bar x)\big)_{\bar x\in f^{-1}(0)}$.

Die Sphärenschar wird durch die Gleichungen

$\begin{matrix} \|x-\bar x\|^2 &=& d^2\\ f(\bar x) &=& 0 \end{matrix}$

beschrieben.

Die Enveloppe hat in jedem Punkt $x\in A$ mit einer der Sphären (parametrisiert durch $\bar x$) den Tangentialraum im Punkt x gemeinsam. Die Tangentialvektoren $dx\in\mathbb{R}^n$ an die Sphäre $S_d(\bar x)$ im Punkt x genügen den Gleichungen

$\begin{matrix} (1)&&f(\bar x) &=& 0,\\ (2)&&\|x-\bar x\|^2&=& d^2,\\ (3)&\quad&(x-\bar x)^T dx &=& 0. \end{matrix}$

Bei der Enveloppe ändert sich im Allgemeinen auch der Scharparameter $\bar x$. Damit ergeben sich für die Tangentialvektoren der Enveloppe außer den Gleichungen (1) und (2) mit $d\bar x\in\mathbb{R}^n$ noch die Gleichungen

$\begin{matrix} (4)&\quad&(x-\bar x)^T (dx- d\bar x) &=& 0,\\ (5)&&f'(\bar x)\; d\bar x &=& 0. \end{matrix}$

Aus (3) und (4) folgt

$(6)\quad(x-\bar x)^T d\bar x = 0$

für alle $d\bar x$ die zu Tangentialvektoren dx im Tangentialraum der Enveloppe korrespondieren, wegen (5) also für alle

$d\bar x \in \ker f'(\bar x) = \left(\operatorname{image}\left(f'(\bar x)^T\right)\right)^{\perp}.$

Nach (6) ergibt sich daraus

$(x-\bar x) \in \left(\left(\operatorname{image}(f'(\bar x)^T\right)^{\perp}\right)^{\perp}=\operatorname{image}(f'(\bar x)^T),$

woraus folgt, dass es $\lambda\in\mathbb{R}^r$ mit

$(7)\quad (x-\bar x) = f'(\bar x)^T \lambda$

gibt.

Mit (1),(2) und (7) hat man n + r + 1 skalare Gleichungen für die 2n + r Unbekannten $x,\bar x,\lambda$. Unter den gemachten Voraussetzungen definieren diese Gleichungen also eine n − 1-dimensionale Mannigfaltigkeit, die dann gerade die Enveloppe der Sphärenschar -- sprich die Äquidistante ist.

Alternative geometrische Interpretation: Die Vektoren $\left(f'_k(\bar x)\right)^T$ $(k=1,\ldots,r)$ bilden eine maximale Menge linear unabhängiger Normalenvektoren auf der Mannigfaltigkeit f ^{− 1}(0) im Punkt $\bar x$. Damit besagt Gleichung (7), dass der Vektor $(x-\bar x)$ vom Punkt $\bar x$ zum zugehörigen Punkt x auf der Äquidistanten genau senkrecht auf der Mannigfaltigkeit f ^{− 1}(0) steht und Gleichung (2), dass der Punkt x den Abstand d von f ^{− 1}(0) haben soll.

Anwendungsbeispiele

Wankelmotor

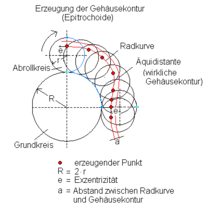
1. Anwendung im Formenbau: Für die Herstellung von Massenartikeln werden häufig Gießverfahren (Spritzgießen, Druckgießen, Kokillenguss usw,) angewendet. Die Gussform hat im Innern die negative Kontur des herzustellenden Artikels als Hohlraum. Für viele Artikel ist eine konstante Wandstärke ausschlaggebend. Daher hat die Beherrschung der Äquidistante in diesem Bereich eine große Bedeutung.
2. Die Äquidistanten-Funktion wird von den meisten CAD-Systemen angeboten. Beispielsweise heißt bei AUTOCAD der deutsche Befehl „versetzen“. Damit kann man beispielsweise sehr schnell eine Dränage mit vorgegebenen Abstand rund um ein Haus festlegen.
3. Beim Wankelmotor ist die Hüllkurve der Trochoide (Radkurve) des Rotors im Abstand d eine Äquidistante.