Datei:Quadratic Golden Mean Siegel Disc IIM.png
Zur Navigation springen
Zur Suche springen
Größe dieser Vorschau: 800 × 587 Pixel. Weitere Auflösungen: 320 × 235 Pixel | 640 × 469 Pixel | 1.024 × 751 Pixel | 1.280 × 939 Pixel | 1.500 × 1.100 Pixel
Originaldatei (1.500 × 1.100 Pixel, Dateigröße: 27 KB, MIME-Typ: image/png)
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
| Beschreibung |
English: Numerical aproximation of Julia set. Map is complex quadratic polynomial. Parameter c is on boundary of main cardioid of period one component of Mandelbrot set with rotational number ( internal angle ) = Golden Mean. Made with modified inverse iteration method MIIM/J with hit limit. It contains Siegel disc Polski: Numeryczna przybliżenie zbioru Julii |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Adam majewski |
| Andere Versionen |
|
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
Diese Datei ist unter der Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 nicht portiert“ lizenziert.
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Beschreibung
This image shows main component of Julia set and its preimages under complex quadratic polynomial[1] up to level 100008 ( new code ) or 25 ( old code).
Main component of Julia set :
- contains Siegel disc ( around fixed point )
- its boundary = critical orbit
- it is a limit of iterations for every other component of filled Julia set
computing c parameter
Parameter c is on boundary of period one component of Mandelbrot set ( = main cardioid ) with combinatorial rotation number ( internal angle ) = inverse Golden Mean[2] .
As a result one gets function describing relation between parameter c and internal angle :
One can compute boundary point c
of period 1 hyperbolic component ( main cardioid) for given internal angle ( rotation number) t using this code by Wolf Jung[3]
phi *= (2*PI); // from turns to radians
cx = 0.5*cos(phi) - 0.25*cos(2*phi);
cy = 0.5*sin(phi) - 0.25*sin(2*phi);
Algorithm
- draw critical orbit = forward orbit of critical point ( "Iterates of critical point delineate a Siegel disc"[4])
- for each point of critical orbit draw all its preimages up to LevelMax if Hit<HitLimit
Critical orbit in this case is : dense [5]( correct me if I'm wrong ) in boundary of component of filled-in Julia set containing Siegel disc.[6]
Mathemathical description
Description [7]
Quadratic polynomial [8] whose variable is a complex number
contains invariant Siegel disc :
Boundary of Siegel disc
- contains critical point :
- is a Jordan curve
- is invariant under quadratic polynomial :
- is a closure of forward orbits of critical points
Julia is build from preimages of boundary of Siegel disc ( union of copies of B meeting only at critical point and it's preimages ):[9]
Here maximal level is not infinity but finite number :
jMax = LevelMax = 100008;
Code efficiency
Recursion
This code uses recursion[10] inside DrawPointAndItsInverseOrbit function so its runing time is (if I'm not wrong ) exponential [11] For level about 25 old code needs 24 hours and for level LevelMax new code needs 37m50.959.
Number of points
| Level | New components | All components | New points | All points |
|---|---|---|---|---|
| 0 | 1 | 1 | NrOfCrOrbitPoints | NrOfCrOrbitPoints |
| 1 | 1 | 2 | NrOfCrOrbitPoints | 2*NrOfCrOrbitPoints |
| 2 | 2 | 4 | ||
| 3 | 4 | 8 | ||
| 4 | 8 | 16 | ||
| ... | ... | ... | ... | |
| 100008 | ||||
| j |
Components gets smaller as level increases ( but with some varioations) so nr of points to draw can be diminished.
C src code
Src code was formatted with Emacs
| old C source code IIM/J ( all) - click on the right to view |
|---|
| a.c: |
/*
c console program
It can be compiled and run under Linux, windows, Mac
It needs gcc
--------------------------------------
draws Julia set for f(z)=z*z+c using IIM
( Inverse Iteration Method )
draws all points up to level
------------------------------------------
mogrify -format gif *.pgm // convert all our PGM images to the gif format:
convert -delay 100 -loop 0 *.gif animated.gif // make animated gif
convert -delay 100 -loop 0 %d.gif[0-10] a10.gif
one can change :
- LevelMax
- iSide ( width of image = iXmax = (15*iSide) it also changes IterationMax = (iXmax*50)
- NrOfCrOrbitPoints = 10 * iXmax;
-----------------------------------------
1.pgm file code is based on the code of Claudio Rocchini
http://en.wikipedia.org/wiki/Image:Color_complex_plot.jpg
create 8 bit color graphic file , portable gray map file = pgm
see http://en.wikipedia.org/wiki/Portable_pixmap
to see the file use external application ( graphic viewer)
I think that creating graphic can't be simpler
---------------------------
2. first it creates data array which is used to store color values of pixels,
fills tha array with data and after that writes the data from array to pgm file.
It alows free ( non sequential) acces to "pixels"
-------------------------------------------
Here are 4 items :
1. complex plane Z with points z = zx+zy*i ( dynamic plane and world coordinate )
2. virtual 2D array indexed by iX and iYmax ( integer or screen coordinate )
3. memory 1D array data indexed by i =f(iX,iY)
4. pgm file
Adam Majewski fraktal.republika.pl
to compile :
gcc a.c -lm -Wall
to run ( Linux console) :
./a.out
NrOfPoints = 15000 File 0.pgm
NrOfPoints = 44999 File 1.pgm
NrOfPoints = 104998 File 2.pgm
NrOfPoints = 224997 File 3.pgm
NrOfPoints = 464996 File 4.pgm
NrOfPoints = 944995 File 5.pgm
NrOfPoints = 1904994 File 6.pgm
NrOfPoints = 3824993 File 7.pgm
NrOfPoints = 7664992 File 8.pgm
NrOfPoints = 15344991 File 9.pgm
NrOfPoints = 30704990 File 10.pgm
NrOfPoints = 61424989 File 11.pgm
NrOfPoints = 61439999 File 12.pgm
NrOfPoints = 184319998 File 13.pgm
NrOfPoints = 430079997 File 14.pgm
NrOfPoints = 921599996 File 15.pgm
NrOfPoints = 1904639995 File 16.pgm
NrOfPoints = 3870719994 File 17.pgm
NrOfPoints = 3507912697 File 18.pgm
NrOfPoints = 2782298104 File 19.pgm
NrOfPoints = 1331068919 File 20.pgm
NrOfPoints = 1392508927 File 21.pgm
NrOfPoints = 4177526782 File 22.pgm
NrOfPoints = 1157627901 File 23.pgm
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
/* iXmax/iYmax = 11/15 */
const int iSide = 100;
int iXmax ; /* width of image in pixels = (15*iSide); */
int iYmax ;
int iLength ;
/* */
const double ZxMin = -1.5;
const double ZxMax = 1.5;
const double ZyMin = -1.1;
const double ZyMax = 1.1;
/* (ZxMax-ZxMin)/(ZyMax-ZyMin)= iXmax/iYmax */
double PixelWidth ;
double PixelHeight ;
unsigned int NrOfPoints = 0;
unsigned int NrOfCrOrbitPoints ;
unsigned int LevelMax = 30; /* nr of points = sum(2^LevelMax) */
/* fc(z) = z*z + c */
/* Golden_Mean_Quadratic_Siegel_Disc */
const double Cx = -0.390540870218399; /* C = Cx + Cy*i */
const double Cy = -0.586787907346969;
/* colors */
const unsigned int MaxColorComponentValue=255; /* color component is coded from 0 to 255 ; it is 8 bit color file */
const int iExterior = 245; /* exterior of Julia set */
const int iJulia = 0; /* border , boundary*/
const int iInterior = 230;
/* ----------------------- functions ---------------------------------------- */
/* gives sign of number */
double sign(double d)
{
if (d<0)
{return -1.0;}
else {return 1.0;};
};
unsigned int f(unsigned int iX, unsigned int iY)
/*
gives position of point (iX,iY) in 1D array ; uses also global variables
it does not check if index is good so memory error is possible
*/
{return (iX + (iYmax- iY-1)*iXmax );}
int DrawPoint( double Zx, double Zy, unsigned char data[])
{
unsigned int iX,iY; /* indices of 2D virtual array (image) = integer coordinate */
unsigned int index; /* index of 1D array */
iX = (int)((Zx-ZxMin)/PixelWidth);
iY = (int)((Zy-ZyMin)/PixelHeight);
index = f(iX,iY);
data[index] = iJulia; /* draw */
NrOfPoints += 1 ;
return 0;
}
int DrawPointAndItsInverseOrbit( double Zx, double Zy, unsigned int LevelMax, unsigned char data[])
{
double NewZx, NewZy;
unsigned int Level = 1;
/* draw point */
DrawPoint(Zx,Zy,data);
/* compute and draw all preimages up to LevelMax */
while (Level<LevelMax)
{
/* Zn*Zn=Z(n+1)-c */
Zx=Zx-Cx;
Zy=Zy-Cy;
/* sqrt of complex number algorithm from Peitgen, Jurgens, Saupe: Fractals for the classroom */
if (Zx>0)
{
NewZx=sqrt((Zx+sqrt(Zx*Zx+Zy*Zy))/2);
NewZy=Zy/(2*NewZx);
}
else /* ZX <= 0 */
{
if (Zx<0)
{
NewZy=sign(Zy)*sqrt((-Zx+sqrt(Zx*Zx+Zy*Zy))/2);
NewZx=Zy/(2*NewZy);
}
else /* Zx=0 */
{
NewZx=sqrt(fabs(Zy)/2);
if (NewZx>0) NewZy=Zy/(2*NewZx);
else NewZy=0;
}
};
DrawPoint(NewZx,NewZy,data);
/* save point and its level to the stack */
DrawPointAndItsInverseOrbit(-NewZx,-NewZy,LevelMax - Level ,data);
/* */
Zx=NewZx;
Zy=NewZy;
Level+=1;
}
/* draw points from stack */
return 0;
}
int Draw(unsigned int pointMax, unsigned int LevelMax, unsigned char data[])
{
unsigned int point; /* nr of point of critical orbit */
double Zx,Zy;
double Zx2,Zy2;
/* critical point z = 0 */
Zx = 0.0;
Zy = 0.0;
DrawPointAndItsInverseOrbit(Zx,Zy,LevelMax,data);
Zx2=Zx*Zx;
Zy2=Zy*Zy;
/* forward orbit of critical point = critical orbit */
for (point=2;point<=pointMax ;point++)
{
/* f(z) = z*z+c */
Zy=2*Zx*Zy + Cy;
Zx=Zx2-Zy2 +Cx;
Zx2=Zx*Zx;
Zy2=Zy*Zy;
/* draws critical orbit */
DrawPoint(Zx,Zy,data); /* main component with Siegel Disc */
/* symmetric point for each point of critical orbit */
/* recurrence version is easy to do */
if (LevelMax>0) DrawPointAndItsInverseOrbit(-Zx,-Zy, LevelMax, data);
// printf(" row %u from %u \n",point, pointMax); /* progres info */
}
return 0;
}
/* --------------------------------------------------------------------------------------------------------- */
int main(){
unsigned int level;
/* unsigned int iX,iY; indices of 2D virtual array (image) = integer coordinate */
iXmax = (15*iSide); /* height of image in pixels */
iYmax = (11*iSide);
iLength = (iXmax*iYmax);
NrOfCrOrbitPoints = 10 * iXmax;
PixelWidth = ((ZxMax-ZxMin)/iXmax);
PixelHeight = ((ZyMax-ZyMin)/iYmax);
/* dynamic 1D arrays for colors ( shades of gray ) and hits */
unsigned int index; /* index of 1D array */
unsigned char *data;
data = malloc( iLength * sizeof(unsigned char) );
if (data == NULL )
{
fprintf(stderr," Could not allocate memory");
return 1;
}
else printf(" memory is OK\n");
for (level=0;level<=LevelMax ;level++)
{
for(index=0;index<iLength-1;++index) data[index]=iExterior; /* clear data */
/* ------------------ draw ----------------------- */
//printf(" Draw %u points of critical orbit and its preimages \n",NrOfCrOrbitPoints);
Draw(NrOfCrOrbitPoints,level, data);
printf(" NrOfPoints = %u \n", NrOfPoints);
/* ---------- file -------------------------------------*/
//printf(" save data array to the pgm file \n");
FILE * fp;
char name [10]; /* name of file */
sprintf(name,"%u",level); /* */
char *filename =strcat(name,".pgm");
char *comment="# C= ";/* comment should start with # */
/* save image to the pgm file */
fp= fopen(filename,"wb"); /*create new file,give it a name and open it in binary mode */
fprintf(fp,"P5\n %s\n %u\n %u\n %u\n",comment,iXmax,iYmax,MaxColorComponentValue); /*write header to the file*/
fwrite(data,iLength,1,fp); /*write image data bytes to the file in one step */
printf("File %s saved. \n", filename);
fclose(fp);
} /* level */
/* --------------free memory ---------------------*/
free(data);
return 0;
}
|
New c code : MIIM/J ( hit limit )
| New C source code - click on the right to view |
|---|
| a.c: |
/*
c console program
It can be compiled and run under Linux, windows, Mac
It needs gcc
--------------------------------------
draws Julia set for f(z)=z*z+c using IIM
( Inverse Iteration Method )
it is based on draw all preimages version
modifications - hits table : if (hits[index]<HitMax)
------------------------------------------
one can change :
- LevelMax
- HitMax
- iSide ( width of image = iXmax = (15*iSide) it also changes IterationMax = (iXmax*50)
- NrOfCrOrbitPoints = 10 * iXmax;
-----------------------------------------
1.pgm file code is based on the code of Claudio Rocchini
http://en.wikipedia.org/wiki/Image:Color_complex_plot.jpg
create 8 bit color graphic file , portable gray map file = pgm
see http://en.wikipedia.org/wiki/Portable_pixmap
to see the file use external application ( graphic viewer)
I think that creating graphic can't be simpler
---------------------------
2. first it creates data array which is used to store color values of pixels,
fills tha array with data and after that writes the data from array to pgm file.
It alows free ( non sequential) acces to "pixels"
-------------------------------------------
Here are 4 items :
1. complex plane Z with points z = zx+zy*i ( dynamic plane and world coordinate )
2. virtual 2D array indexed by iX and iYmax ( integer or screen coordinate )
3. memory 1D array data indexed by i =f(iX,iY)
4. pgm file
Adam Majewski fraktal.republika.pl
to compile :
gcc h.c -lm -Wall
to run ( Linux console) :
./a.out
File 15.pgm saved.
gcc h.c -lm -Wall real 0m1.886s
gcc h.c -lm -Wall -O2 real 0m1.651s
gcc h.c -lm -Wall -O3 real 0m1.594s
NrOfPoints = 160 753 417
File L100005.pgm saved real 27m16.199s
NrOfPoints = 341551869
File L100008.pgm saved. real 37m50.959s
convert -version
convert L100008.pgm -resize 1500x1100 m1500.png
convert L100008.pgm -resize 1500x1100 -convolve "-0.125,0,0.125, -0.25,0,0.25, -0.125,0,0.125" -negate 1500d.png
convert L100008.pgm -resize 1500x1100 -convolve "-1,0,1,-2,0,2,-1,0,1" -convolve "-1,-2,-1,0,0,0,1,2,1" 1500en.png
convert L100008.pgm -resize 1500x1100 -convolve "-0.125,0,0.125, -0.25,0,0.25, -0.125,0,0.125" 1500dd.png
convert L100008.pgm -convolve "-0.125,0,0.125, -0.25,0,0.25, -0.125,0,0.125" -resize 1500x1100 -negate 1500e5.png
convert L100008.pgm -resize 1500x1100 -convolve "-1,0,1,-2,0,2,-1,0,1","-1,-2,-1,0,0,0,1,2,1" -negate 1500e2.png
convert L100008.pgm -convolve "-1,-1,-1,-1,8,-1,-1,-1,-1" -resize 1500x1100 1500e6.png
convert L100008.pgm -convolve "-1,-1,-1,-1,8,-1,-1,-1,-1" -resize 1500x1100 -negate 1500e6n.png
convert L100008.pgm -convolve "-1,-1,-1,-1,8,-1,-1,-1,-1" -resize 1500x1100 -threshold 5% -negate 1500e6n95.png
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
unsigned int NrOfPoints = 0;
unsigned int NrOfCrOrbitPoints ;
unsigned int HitMax = 200; /* how many times z can be inside pixel */
unsigned int LevelMax = 100008; /* nr of points = sum(2^LevelMax) */
/* iXmax/iYmax = 11/15 */
const int iSide = 800;
int iXmax ; /* width of image in pixels = (15*iSide); */
int iYmax ;
int iLength ;
/* */
const double ZxMin = -1.5;
const double ZxMax = 1.5;
const double ZyMin = -1.1;
const double ZyMax = 1.1;
/* (ZxMax-ZxMin)/(ZyMax-ZyMin)= iXmax/iYmax */
double PixelWidth ;
double PixelHeight ;
/* fc(z) = z*z + c */
/* Golden_Mean_Quadratic_Siegel_Disc */
const double Cx = -0.390540870218399; /* C = Cx + Cy*i */
const double Cy = -0.586787907346969;
/* colors */
const unsigned int MaxColorComponentValue=255; /* color component is coded from 0 to 255 ; it is 8 bit color file */
const int iExterior = 245; /* exterior of Julia set */
const int iJulia = 0; /* border , boundary*/
const int iInterior = 230;
/* ----------------------- functions ---------------------------------------- */
/* gives sign of number */
double sign(double d)
{
if (d<0)
{return -1.0;}
else {return 1.0;};
};
unsigned int f(unsigned int iX, unsigned int iY)
/*
gives position of point (iX,iY) in 1D array ; uses also global variables
it does not check if index is good so memory error is possible
*/
{return (iX + (iYmax- iY-1)*iXmax );}
int DrawPoint( double Zx, double Zy, unsigned char data[], unsigned char hits[])
{
unsigned int iX,iY; /* indices of 2D virtual array (image) = integer coordinate */
unsigned int index; /* index of 1D array */
/* I do not why but some points escape ; I cant find an error but it is
probably in code for finding preimages */
if (Zx>ZxMax || Zx<ZxMin || Zy>ZyMax || Zy<ZyMin) return 1; /* stop */
iX = (int)((Zx-ZxMin)/PixelWidth);
iY = (int)((Zy-ZyMin)/PixelHeight);
index = f(iX,iY);
if (hits[index]>HitMax) return 1; /* stop if pixel is hit to often */
data[index] = iJulia; /* draw */
hits[index] +=1;
NrOfPoints += 1 ;
return 0;
}
int DrawPointAndItsInverseOrbit( double Zx, double Zy, unsigned int LevelMax, unsigned char data[], unsigned char hits[])
{
double NewZx, NewZy;
unsigned int Level = 1; /* start from 1 to LevelMax */
/* draw point */
DrawPoint(Zx,Zy,data, hits);
/* compute and draw all preimages up to LevelMax */
while (Level<LevelMax)
{
/* Zn*Zn=Z(n+1)-c */
Zx=Zx-Cx;
Zy=Zy-Cy;
/* sqrt of complex number algorithm from Peitgen, Jurgens, Saupe: Fractals for the classroom */
if (Zx>0.0)
{ NewZx=sqrt((Zx+sqrt(Zx*Zx+Zy*Zy))/2);
NewZy=Zy/(2*NewZx); }
else /* ZX <= 0 */
{
if (Zx<0.0)
{ NewZy=sign(Zy)*sqrt((-Zx+sqrt(Zx*Zx+Zy*Zy))/2);
NewZx=Zy/(2*NewZy); }
else /* Zx=0 */
{ NewZx=sqrt(fabs(Zy)/2);
if (NewZx>0) NewZy=Zy/(2*NewZx);
else NewZy=0.0; }
};
/* I do not why but some points escape ; I cant find an error but it is
probably in code for finding preimages */
/* first check point if not escaping and hit<hit limit then draw it */
if( DrawPoint(NewZx,NewZy,data, hits))
{ DrawPoint(-NewZx,-NewZy,data, hits);
Level=LevelMax; /* else stop this subtree */
}
DrawPointAndItsInverseOrbit(-NewZx,-NewZy,LevelMax - Level ,data, hits);
Zx=NewZx;
Zy=NewZy;
Level+=1;
}
return 0;
}
int DrawJulia(unsigned int pointMax, unsigned int LevelMax, unsigned char data[] , unsigned char hits[])
{
unsigned int point; /* nr of point of critical orbit */
double Zx,Zy;
double Zx2,Zy2;
/* critical point z = 0 */
Zx = 0.0;
Zy = 0.0;
DrawPointAndItsInverseOrbit(Zx,Zy,LevelMax,data, hits);
Zx2=Zx*Zx;
Zy2=Zy*Zy;
/* forward orbit of critical point = critical orbit */
for (point=2;point<=pointMax ;point++)
{
/* f(z) = z*z+c */
Zy=2*Zx*Zy + Cy;
Zx=Zx2-Zy2 + Cx;
Zx2=Zx*Zx;
Zy2=Zy*Zy;
/* draws critical orbit */
DrawPoint(Zx,Zy,data, hits); /* main component with Siegel Disc */
/* symmetric point for each point of critical orbit */
if (LevelMax>0) DrawPointAndItsInverseOrbit(-Zx,-Zy, LevelMax, data, hits);
printf(" %u / %u \n",point, pointMax); /* progres info */
}
return 0;
}
/* --------------------------------------------------------------------------------------------------------- */
int main(){
/* unsigned int iX,iY; indices of 2D virtual array (image) = integer coordinate */
iXmax = (15*iSide); /* height of image in pixels */
iYmax = (11*iSide);
iLength = (iXmax*iYmax);
NrOfCrOrbitPoints = 2000 * iXmax;
PixelWidth = ((ZxMax-ZxMin)/iXmax);
PixelHeight = ((ZyMax-ZyMin)/iYmax);
/* dynamic 1D arrays for colors ( shades of gray ) and hits */
unsigned int index; /* index of 1D array */
unsigned char *data;
unsigned char *hits;
data = malloc( iLength * sizeof(unsigned char) );
hits = malloc( iLength * sizeof(unsigned char) );
if (data == NULL || hits==NULL )
{
fprintf(stderr," Could not allocate memory");
return 1;
}
else printf(" memory is OK\n");
printf(" clear the arrays \n");
for(index=0;index<iLength-1;++index)
{ data[index]=iExterior;
hits[index]=0; }
/* ------------------ draw ----------------------- */
printf(" Draw Julia set = %u points of critical orbit and its preimages \n",NrOfCrOrbitPoints);
DrawJulia(NrOfCrOrbitPoints,LevelMax, data, hits);
printf(" NrOfPoints = %u \n", NrOfPoints);
/* ---------- file -------------------------------------*/
printf(" save data array to the pgm file \n");
FILE * fp;
char name [20]; /* name of file */
sprintf(name,"L%u",LevelMax); /* */
char *filename =strcat(name,".pgm");
char *comment="# C= ";/* comment should start with # */
/* save image to the pgm file */
fp= fopen(filename,"wb"); /*create new file,give it a name and open it in binary mode */
fprintf(fp,"P5\n %s\n %u\n %u\n %u\n",comment,iXmax,iYmax,MaxColorComponentValue); /*write header to the file*/
fwrite(data,iLength,1,fp); /*write image data bytes to the file in one step */
printf("File %s saved. \n", filename);
fclose(fp);
/* --------------free memory ---------------------*/
free(data);
free(hits);
return 0;
}
|
Postprocessing
Using Image Magic :
- edge detection
- resize
- convert to black and white image
- inversion
convert L100008.pgm -convolve "-1,-1,-1,-1,8,-1,-1,-1,-1" -resize 1500x1100 -threshold 5% -negate 1500e6n95.png
Compare with
-
Animated version -
Average velocity - color version -
Average velocity - gray version -
Orbits inside Siegel Disc -
other Siegel disc using IIM -
other Siegel disc using DEM
References
- ↑ complex quadratic polynomial
- ↑ wikipedia : Golden ratio
- ↑ Mandel: software for real and complex dynamics by Wolf Jung
- ↑ Complex Dynamics by Lennart Carleson and Theodore W. Gamelin. Page 84
- ↑ Dense set in wikipedia
- ↑ Joachim Grispolakis, John C. Mayer and Lex G. Oversteegen Journal: Trans. Amer. Math. Soc. 351 (1999), 1171-1201
- ↑ A. Blokh, X. Buff, A. Cheritat, L. Oversteegen The solar Julia sets of basic quadratic Cremer polynomials, Ergodic Theory and Dynamical Systems , 30 (2010), #1, 51-65,
- ↑ wikipedia : Complex quadratic polynomial
- ↑ Building blocks for Quadratic Julia sets by : Joachim Grispolakis, John C. Mayer and Lex G. Oversteegen Journal: Trans. Amer. Math. Soc. 351 (1999), 1171-1201
- ↑ wikipedia : Recursion
- ↑ Big O notation in wikipedia
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 18:39, 17. Nov. 2011 | | 1.500 × 1.100 (27 KB) | Soul windsurfer | New version : new code and new conversion |
| 10:38, 16. Nov. 2011 | 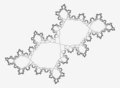 | 1.500 × 1.100 (39 KB) | Soul windsurfer | 25 level - 2 days !!! ( I must improve program) | |
| 15:28, 13. Nov. 2011 |  | 1.500 × 1.100 (39 KB) | Soul windsurfer |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
Globale Dateiverwendung
Die nachfolgenden anderen Wikis verwenden diese Datei:
- Verwendung auf ar.wikipedia.org
- Verwendung auf en.wikipedia.org
- Verwendung auf en.wikibooks.org
