Bikonditional
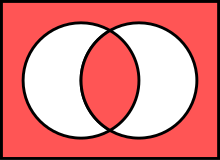
Das Bikonditional ist die Negation des ausschließenden Oder und bedeutet „beide nicht oder beide“.
Dem entsprechen die roten Bereiche außerhalb und innerhalb beider Kreise.
Als Bikonditional, Bisubjunktion oder materiale Äquivalenz, manchmal (aber mehrdeutig) einfach nur Äquivalenz bezeichnet man
- eine zusammengesetzte Aussage, die genau dann wahr ist, wenn ihre beiden Teilaussagen denselben Wahrheitswert haben, also entweder beide wahr oder beide falsch sind;
- die entsprechend definierte Wahrheitswertfunktion;
- das sprachliche Zeichen (den Junktor), mit dem diese beiden Teilaussagen zusammengesetzt werden.
In der Aussagenlogik spricht man von einer Exklusiv-NICHT-ODER-Verknüpfung (auch XNOR, NXOR oder Äquivalenz). Die Gesamtaussage ist auch wahr, wenn entweder alle Teilaussagen wahr oder alle falsch sind. Anders formuliert ist eine (binäre) XNOR-Verknüpfung genau dann wahr, wenn beide Teilaussagen den gleichen Wahrheitswert liefern. Die XNOR-Verknüpfung ist entsprechend eine XOR-Verknüpfung gefolgt von einer Negation.
Schreibweise und Lesart
[Bearbeiten | Quelltext bearbeiten]Als Zeichen für das Bikonditional als Junktor wird meist der Äquivalenzpfeil ↔, der dreifache Querstrich oder der Doppelpfeil mit zwei Querlinien verwendet, gelegentlich auch die Tilde ~. (Fast jedes dieser Zeichen wird von unterschiedlichen Autoren und in unterschiedlichen Zusammenhängen auch in anderer Bedeutung verwendet, am häufigsten die Tilde für die Satzverneinung und der Doppelpfeil mit zwei Querlinien für die metasprachliche Äquivalenz.) In der polnischen Notation wird das Bikonditional durch den Großbuchstaben E ausgedrückt.
In der natürlichen Sprache gibt es mehrere Möglichkeiten, ein Bikonditional auszudrücken, zum Beispiel die Formulierungen „A genau dann, wenn B“ (abgekürzt als „A gdw. B“), „A dann und nur dann, wenn B“ oder „A ist hinreichend und notwendig für B“; auch die im Englischen verwendete Formulierung „A if and only if B“ findet sich abgekürzt als „A iff B“ gelegentlich sogar in deutschsprachigen Texten. Jede dieser Formulierungen ist dazu geeignet, den Ausdruck zu lesen.
Bedeutung
[Bearbeiten | Quelltext bearbeiten]Für die zweiwertige, wahrheitsfunktionale klassische Logik ist der Wahrheitswertverlauf (die Wahrheitstabelle) und damit die Bedeutung des Bikonditionals wie folgt durch die äq-Funktion definiert („w“ steht für „wahr“; „f“ steht für „falsch“):
| P | Q | |
|---|---|---|
| w | w | w |
| w | f | f |
| f | w | f |
| f | f | w |
In der klassischen Logik sind die Aussagen und (das heißt die Konjunktion des Konditionals und des Konditionals ) äquivalent, das heißt, sie haben denselben Wahrheitswerteverlauf. Aus diesem Grund wird das Bikonditional oft nicht als selbstständiger Junktor eingeführt, sondern durch folgende Definition auf Konjunktion und Konditional zurückgeführt:
Dabei sei „:=“ das metasprachliche Zeichen für „sei definiert als“ und seien und metasprachliche Satzvariablen, also Platzhalter, die für beliebige Sätze der logischen Objektsprache stehen dürfen. Als konkretes Beispiel würde der Ausdruck gemäß dieser Definition aufgelöst zu .
Obige Äquivalenz und obige Definierbarkeit zeigen insbesondere, dass das Bikonditional eine hinreichende und notwendige Bedingung ausdrückt: sagt aus, dass A eine hinreichende Bedingung für B und dass B eine notwendige Bedingung für A ist; und sagt aus, dass B eine hinreichende Bedingung für A und dass A eine notwendige Bedingung für B ist.
Beispiele
[Bearbeiten | Quelltext bearbeiten]- ist ein Bikonditional, das immer wahr ist. Es ist also eine Tautologie.
- ist ein Bikonditional, das niemals wahr ist.
- ist ein Bikonditional, das wahr oder falsch sein kann, je nachdem, wie es um die Wahrheit der Teilaussagen A, B, C steht.
- „Der Mond ist genau dann eine Lichtquelle, wenn Isaak Newton ein Deutscher war“ ist ein wahres Bikonditional, ebenso: „Der Mars ist genau dann ein Planet, wenn die Ozeane Salz enthalten.“[1] Dieses Beispiel zeigt, dass die Paradoxien der materialen Implikation analog beim Bikonditional auftreten: Es kann wahr sein, ohne dass irgendein inhaltlicher Zusammenhang zwischen den beiden Aussagen besteht.
Zweideutigkeit für mehrere Argumente
[Bearbeiten | Quelltext bearbeiten]Werden mehr als zwei Argumente durch verbunden, ist nicht eindeutig, wie die Formel gemeint ist:
kann die Abkürzung für sein,
oder dafür, dass alle entweder zusammen wahr oder zusammen falsch sind:
Das ist nur für zwei Argumente das Gleiche. Die beiden Wahrheitstafeln zeigen nur in Zeilen mit zwei Argumenten das gleiche Bitmuster:

im Sinne von
Das mittlere Venn-Diagramm unten
und Zeile (ABC ) in dieser Matrix
stehen für die gleiche Operation.

als Abkürzung für
Das rechte Venn-Diagramm unten
und Linie (ABC ) in dieser Matrix
stehen für die gleiche Operation.
Das linke Venn-Diagramm unten und die Zeilen (AB ) in diesen Matrizen stehen für die gleiche Operation.
Venn-Diagramme
[Bearbeiten | Quelltext bearbeiten]Rote Flächen stehen für die Wahrheit (wie beispielsweise in ![]() für und).
für und).
|
|
|
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ beide Beispiele entnommen aus Wesley C. Salmon: Logik. Reclam, Stuttgart 1983, ISBN 3-15-007996-9, Seite 81.



































