Formfaktor (Elektrotechnik)
In der elektrischen Messtechnik ist der Formfaktor das Verhältnis von Effektivwert zu Gleichrichtwert eines Signals. Sein Wert im Bereich von eins bis unendlich hängt von der Kurvenform ab.
Allgemeines[Bearbeiten | Quelltext bearbeiten]
Für den Formfaktor einer Größe, in diesem Fall ist als Größe die elektrischen Spannung gewählt, mit der Periodendauer gilt:
Der Formfaktor ist insbesondere bei der Messung von Wechselgrößen von Bedeutung, da zwar üblicherweise der Effektivwert angezeigt werden soll, allerdings bei einfacheren Messgeräten nur der Gleichrichtwert erfasst wird. Diese Geräte zeigen das 1,11-Fache des Gleichrichtwertes an, das heißt, sie sind justiert auf den Formfaktor eines Sinussignals
Bei anderen Signalformen (Dreieck, Rechteck etc.) mit anderen Formfaktoren wird so der Messwert verfälscht.
Bei Mischgrößen ist es in manchen Situationen sinnvoll, den Formfaktor statt für das gesamte Signal lediglich für seinen Wechselanteil anzugeben.
Das Verhältnis aus Scheitelwert zu Effektivwert wird als Scheitelfaktor oder Crestfaktor bezeichnet.
Formfaktoren[Bearbeiten | Quelltext bearbeiten]
Folgende Tabelle zeigt Formfaktoren und verwandte Größen für verschiedene einfache Signalformen. Sie sind alle unabhängig vom Scheitelwert.
| Schwingungsart | Schwingungsform | Gleichrichtwert bezogen auf Scheitelwert |
Formfaktor | Effektivwert durch Scheitelwert |
Scheitelfaktor |
|---|---|---|---|---|---|
| Sinusschwingung |  |
||||
| Volle Schwingung gleichgerichteter Sinus |
 |
||||
| Halbschwingung gleichgerichteter Sinus |
 |
||||
| Dreieckschwingung | 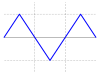 |
||||
| Sägezahnschwingung |  |
||||
| Symmetrische Rechteckschwingung |
 |
||||
| PDM-Signal | 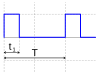 |
||||
| Gleichgröße |
Literatur[Bearbeiten | Quelltext bearbeiten]
- R. Patzelt, H. Fürst: Elektrische Meßtechnik. Springer, 1993, ISBN 3-211-82442-1.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Measurements of AC Magnitude. Abgerufen am 30. Dezember 2012.



















