k-Means-Algorithmus
Ein k-Means-Algorithmus ist ein Verfahren zur Vektorquantisierung, das auch zur Clusteranalyse verwendet wird. Dabei wird aus einer Menge von ähnlichen Objekten eine vorher bekannte Anzahl von k Gruppen gebildet. Der Algorithmus ist eine der am häufigsten verwendeten Techniken zur Gruppierung von Objekten, da er schnell die Zentren der Cluster findet. Dabei bevorzugt der Algorithmus Gruppen mit geringer Varianz und ähnlicher Größe.
Der Algorithmus hat starke Ähnlichkeiten mit dem EM-Algorithmus und zeichnet sich durch seine Einfachheit aus.[1] Erweiterungen sind der k-Median-Algorithmus und der k-Means++ Algorithmus.
Historische Entwicklung[Bearbeiten | Quelltext bearbeiten]
Der Begriff „k-means“ wurde zuerst von MacQueen 1967 verwendet,[2] die Idee geht jedoch auf Hugo Steinhaus 1957 zurück.[3] Der heutzutage meist als „k-means-Algorithmus“ bezeichnete Standard-Algorithmus wurde 1957 von Lloyd zur Puls-Code-Modulation vorgeschlagen, aber erst 1982 in einer Informatik-Zeitschrift publiziert[4] und deckt sich weitestgehend mit der Methode von Forgy, die 1965 publiziert wurde.[5] Eine weitere Variante ist die von Hartigan und Wong, die unnötige Distanzberechnungen vermeidet, indem sie auch den Abstand zum zweitnächsten Mittelpunkt verwendet.[6][7] Eine genaue Zuordnung der Algorithmen wird oft falsch gemacht: Insbesondere wird oft der Algorithmus von Lloyd/Forgy beschrieben, als Quelle jedoch MacQueen genannt.
Problemstellung[Bearbeiten | Quelltext bearbeiten]
Ziel von k-Means ist es, den Datensatz so in Partitionen zu teilen, dass die Summe der quadrierten Abweichungen von den Cluster-Schwerpunkten minimal ist. Mathematisch entspricht dies der Optimierung der Funktion
mit den Datenpunkten und den Schwerpunkten der Cluster . Diese Zielfunktion basiert auf der Methode der kleinsten Quadrate und man spricht auch von Clustering durch Varianzminimierung,[8] da die Summe der Varianzen der Cluster minimiert wird. Da zudem die quadrierte Euklidische Distanz ist, ordnet k-Means effektiv jedes Objekt dem nächstgelegenen (nach Euklidischer Distanz) Clusterschwerpunkt zu. Umgekehrt ist das arithmetische Mittel ein Kleinste-Quadrate-Schätzer, optimiert also ebenfalls dieses Kriterium.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Da die Suche nach der optimalen Lösung schwer ist (NP-schwer), wird im Normalfall ein approximativer Algorithmus verwendet wie die Heuristiken von Lloyd oder MacQueen. Da die Problemstellung von k abhängig ist, muss dieser Parameter vom Benutzer festgelegt werden. Es existieren jedoch auch Ansätze, durch Verwendung eines zweiten Objektes diesen Parameter zu wählen (vgl. X-Means, Akaike-Informationskriterium, bayessches Informationskriterium und Silhouettenkoeffizient).
Lloyd-Algorithmus[Bearbeiten | Quelltext bearbeiten]

Der am häufigsten verwendete k-Means-Algorithmus ist der Lloyd-Algorithmus, der oft als „der k-means-Algorithmus“ bezeichnet wird, obwohl Lloyd diesen Namen nicht verwendet hat. Lloyds Algorithmus besteht aus drei Schritten:
- Initialisierung: Wähle zufällige Mittelwerte (Means): aus dem Datensatz.
- Zuordnung: Jedes Datenobjekt wird demjenigen Cluster zugeordnet, bei dem die Cluster-Varianz am wenigsten erhöht wird.
- Aktualisieren: Berechne die Mittelpunkte der Cluster neu:
Die Schritte 2–3 werden dabei so lange wiederholt, bis sich die Zuordnungen nicht mehr ändern.
MacQueen’s Algorithmus[Bearbeiten | Quelltext bearbeiten]
MacQueen führte mit dem Begriff „k-Means“ einen anderen Algorithmus ein:
- Wähle die ersten Elemente als Clusterzentren
- Weise jedes neue Element dem Cluster zu, bei dem sich die Varianz am wenigsten erhöht, und aktualisiere das Clusterzentrum
Während es ursprünglich – vermutlich – nicht vorgesehen war, kann man auch diesen Algorithmus iterieren, um ein besseres Ergebnis zu erhalten.
Variationen[Bearbeiten | Quelltext bearbeiten]
- k-Means ++ versucht bessere Startpunkte zu finden.[9]
- Der Filtering-Algorithmus verwendet als Datenstruktur einen k-d-Baum.[10]
- Der k-Means-Algorithmus kann beschleunigt werden unter Berücksichtigung der Dreiecksungleichung.[11]
- Bisecting k-means beginnt mit , und teilt dann immer den größten Cluster, bis das gewünschte k erreicht ist.
- X-means beginnt mit und erhöht so lange, bis sich ein sekundäres Kriterium (Akaike-Informationskriterium, oder bayessches Informationskriterium) nicht weiter verbessert.
Voraussetzungen[Bearbeiten | Quelltext bearbeiten]
k-Means optimiert die quadratischen Abweichungen von einem Mittelwert. Es kann daher nur mit numerischen Attributen verwendet werden, bei denen ein sinnvoller Mittelwert berechnet werden kann. Kategorielle Attribute (bspw. „Auto“, „LKW“, „Fahrrad“) können nicht verwendet werden, da hier kein Mittelwert berechnet werden kann.
Der Parameter , die Anzahl der Cluster, muss im Voraus bekannt sein. Er kann jedoch auch experimentell bestimmt werden. Das Problem ist, dass die verschiedenen Cluster miteinander verglichen werden müssen und die Kostenfunktion mit steigendem monoton sinkt. Eine Lösung ist der Silhouettenkoeffizient, der eine von unabhängige Bewertung von Clusterungen liefert. Hierbei wird nicht nur geprüft, wie weit ein Punkt vom eigenen Clusterschwerpunkt entfernt ist, sondern es gehen auch die Entfernungen von anderen Clusterschwerpunkten in die Bewertung des Clustering mit ein.
Die Cluster im Datensatz müssen etwa gleich groß sein, da der Algorithmus den Datensatz stets an der Mitte zwischen zwei Clusterzentren partitioniert.
Der Datensatz darf nicht viel Rauschen bzw. nicht viele Ausreißer enthalten. Fehlerhafte Datenobjekte verschieben die berechneten Clusterzentren oft erheblich, und der Algorithmus hat keine Vorkehrungen gegen derartige Effekte (vgl. DBSCAN, das „Noise“-Objekte explizit vorsieht).
Probleme[Bearbeiten | Quelltext bearbeiten]

k-Means ist ein leistungsfähiger Algorithmus, jedoch nicht ohne Schwachstellen. Ein k-Means-Algorithmus muss nicht die beste mögliche Lösung finden. Die gefundene Lösung hängt stark von den gewählten Startpunkten ab. Der einfachste Ansatz ist, den Algorithmus mehrmals hintereinander mit verschiedenen Startwerten zu starten und die beste Lösung zu nehmen. Es gibt aber auch viele Überlegungen, wie eine geeignete Verteilung der Startwerte erreicht werden kann. Zu nennen sind unter anderem k-means++, aber auch mit dem Ziehen kleiner Stichproben können die Clusterzentren vor dem Start von k-means angenähert werden. Außerdem macht es einen Unterschied, ob man beliebige Clusterzentren wählt, oder jeden Punkt einem beliebigen Cluster zuordnet und dann die Clusterzentren ermittelt.
Ein weiterer Nachteil ist, dass die Anzahl der Clusterzentren im Voraus gewählt wird. Bei Verwendung eines ungeeigneten können sich komplett andere, unter Umständen unintuitive Lösungen ergeben. Bei einem „falschen“ kann kein gutes Clustering erfolgen. Die Lösung ist, verschiedene Werte für zu probieren und dann ein geeignetes zu wählen, zum Beispiel mit Hilfe des Silhouettenkoeffizienten, oder durch Vergleich der verschiedenen Clusteringkosten.
Gruppen in den Daten können sich, wie in dem gezeigten Schwertlilien-Beispiel, überlappen und nahtlos ineinander übergehen. In einem solchen Fall kann k-Means diese Gruppen nicht zuverlässig trennen, da die Daten nicht dem verwendeten Cluster-Modell folgen.
Des Weiteren sucht k-Means stets konvexe Cluster (bedingt durch die Minimierung des Abstandes zum Clusterschwerpunkt). Andere Algorithmen wie DBSCAN können auch beliebig geformte „dichtebasierte“ Cluster finden. Was ebenfalls von k-Means nicht unterstützt wird, sind hierarchische Cluster (also Cluster, die wiederum eine Clusterstruktur aufweisen), wie sie beispielsweise mit OPTICS gefunden werden können.
Als letztes wird in k-means jeder Punkt einem Cluster zugewiesen, es gibt keine Möglichkeit Ausreißer zu erkennen. Diese können das Ergebnis stark verfälschen. Abhilfe kann hier eine vorherige Noisereduktion schaffen, oder andere Algorithmen, wie DBSCAN, die automatisch Noise erkennen.
Erweiterungen[Bearbeiten | Quelltext bearbeiten]
K-Median[Bearbeiten | Quelltext bearbeiten]
Im k-Median-Algorithmus wird im Zuweisungschritt statt der euklidischen Distanz die Manhattan-Distanz verwendet. Im Updateschritt wird der Median statt des Mittelwerts verwendet.[12][13]
K-Means++[Bearbeiten | Quelltext bearbeiten]
Der k-Means++-Algorithmus wählt die Cluster-Schwerpunkte nicht zufällig, sondern nach folgender Vorschrift:
- Wähle als ersten Cluster-Schwerpunkt zufällig ein Objekt aus
- Für jedes Objekt berechne den Abstand zum nächstgelegenen Cluster-Schwerpunkt
- Wähle zufällig als nächsten Cluster-Schwerpunkt ein Objekt aus. Die Wahrscheinlichkeit, mit der ein Objekt ausgewählt wird, ist proportional zu , d. h. je weiter das Objekt von den bereits gewählten Cluster-Schwerpunkten entfernt ist, desto wahrscheinlicher ist es, dass es ausgewählt wird.
- Wiederhole Schritt 2 und 3 bis Cluster-Schwerpunkte bestimmt sind
- Führe nun den üblichen k-Means Algorithmus aus
In der Regel konvergiert der nachfolgende k-Means Algorithmus in wenigen Schritten. Die Ergebnisse sind so gut wie bei einem üblichen k-Means-Algorithmus, jedoch ist der Algorithmus typischerweise fast doppelt so schnell wie der k-Means-Algorithmus.[14]
K-Medoids (PAM)[Bearbeiten | Quelltext bearbeiten]
Der Algorithmus PAM (Partitioning Around Medoids, Kaufman und Rousseeuw, 1990) – auch bekannt als k-Medoids[15] – kann als Variante des k-Means Algorithmus interpretiert werden, die mit beliebigen Distanzen konvergiert.
- Wähle Objekte als Cluster-Schwerpunkte (Medoid) aus
- Ordne jedes Objekt dem nächsten Cluster-Schwerpunkt zu
- Für jeden Cluster-Schwerpunkt und jeden Nicht-Cluster-Schwerpunkt vertausche die Rollen
- Berechne für jede Vertauschung die Summe der Distanzen oder Unähnlichkeiten
- Wähle als neue Cluster-Schwerpunkte die Vertauschung, die die kleinste Summe liefert
- Wiederhole 2.–5. solange, bis sich die Cluster-Schwerpunkte nicht mehr ändern
In der ursprünglichen Version von PAM macht hierbei der erste Schritt – die Wahl der initialen Medoiden – einen großen Teil des Algorithmus aus. Da in jeder Iteration stets nur die beste Vertauschung durchgeführt wird, ist der Algorithmus nahezu deterministisch (bis auf exakt gleiche Distanzen). Dadurch ist der Algorithmus aber auch meist sehr langsam.
Während k-means die Summe der Varianzen minimiert, minimiert k-Medoids die Distanzen. Insbesondere kann dieser Algorithmus mit beliebigen Distanzfunktionen verwendet werden, und konvergiert dennoch garantiert.
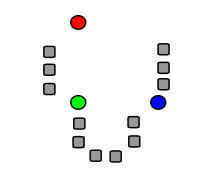
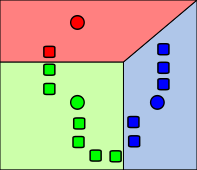
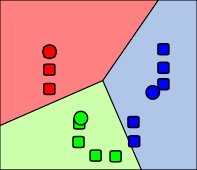
Beispiel[Bearbeiten | Quelltext bearbeiten]
Die folgenden Bilder zeigen exemplarisch einen Durchlauf eines k-Means-Algorithmus zur Bestimmung von drei Gruppen:
Anwendung in der Bildverarbeitung[Bearbeiten | Quelltext bearbeiten]
In der Bildverarbeitung wird der k-Means-Algorithmus oft zur Segmentierung verwendet. Als Entfernungsmaß ist die euklidische Distanz häufig nicht ausreichend und es können andere Abstandsfunktionen, basierend auf Pixelintensitäten und Pixelkoordinaten verwendet werden. Die Ergebnisse werden zur Trennung von Vordergrund und Hintergrund und zur Objekterkennung benutzt. Der Algorithmus ist weit verbreitet und ist in gängigen Bildverarbeitungsbibliotheken wie OpenCV, Scikit-image[16] und itk implementiert.
Software[Bearbeiten | Quelltext bearbeiten]
K-means und seine Varianten sind in verschiedener Open-Source-Software verfügbar.
- Dlib[17]
- ELKI enthält die Varianten von Lloyd und MacQueen, dazu verschiedene Strategien für die Startwerte wie k-means++, und Varianten des Algorithmus wie k-medians, k-medoids und PAM.
- GNU R enthält die Varianten von Hartigan, Lloyd und MacQueen, und zusätzliche Variationen im Erweiterungspaket „flexclust“.
- OpenCV enthält eine auf Bildverarbeitung optimierte Version von k-means (inkl. k-means++ seeding)
- Scikit-learn enthält k-means, inkl. Elkans Variante und k-means++.
- Weka enthält k-means (inkl. k-means++ seeding) und die Erweiterung x-means.
Literatur[Bearbeiten | Quelltext bearbeiten]
- David MacKay: Information Theory, Inference and Learning Algorithms. Cambridge University Press, 2003, ISBN 0-521-64298-1, Chapter 20. An Example Inference Task: Clustering, S. 284–292 (inference.phy.cam.ac.uk [PDF]).
- Gary Bradski, Adrian Kaehler: Learning OpenCV Computer Vision with the OpenCV Library. O’Reilly, 2001, ISBN 978-0-596-51613-0.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Gary Bradski, Adrian Kaehler: Learning OpenCV Computer Vision with the OpenCV Library. O’Reilly, 2001, ISBN 978-0-596-51613-0, S. 479–480.
- ↑ J. B. MacQueen: Some Methods for classification and Analysis of Multivariate Observations. In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. Band 1. University of California Press, 1967, S. 281–297 (projecteuclid.org [abgerufen am 7. April 2009]).
- ↑ Hugo Steinhaus: Sur la division des corps matériels en parties. In: Bull. Acad. Polon. Sci. 12. Auflage. Band 4, 1957, S. 801–804 (französisch).
- ↑
S. P. Lloyd: Least square quantization in PCM. In: Bell Telephone Laboratories Paper. 1957., später erst in einer Zeitschrift:
S. P. Lloyd: Least squares quantization in PCM. In: IEEE Transactions on Information Theory. 2. Auflage. Band 28, 1982, S. 129–137, doi:10.1109/TIT.1982.1056489 (cs.toronto.edu [PDF; 1,3 MB; abgerufen am 15. April 2009]). - ↑ E.W. Forgy: Cluster analysis of multivariate data: efficiency versus interpretability of classifications. In: Biometrics. 21. Auflage. 1965, S. 768–769.
- ↑ J.A. Hartigan: Clustering algorithms. John Wiley & Sons, 1975.
- ↑ J. A. Hartigan, M. A. Wong: Algorithm AS 136: A K-Means Clustering Algorithm. In: Journal of the Royal Statistical Society, Series C (Applied Statistics). 1. Auflage. Band 28, 1979, S. 100–108, JSTOR:2346830.
- ↑ Martin Ester, Jörg Sander: Knowledge Discovery in Databases: Techniken und Anwendungen. Springer, Berlin 2000, ISBN 3-540-67328-8.
- ↑ David Arthur, Sergei Vassilvitskii: K-means++: The Advantages of Careful Seeding. In: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA 2007, ISBN 978-0-89871-624-5, S. 1027–1035 (stanford.edu [PDF; abgerufen am 27. März 2015]).
- ↑ T. Kanungo, D. M. Mount, N. S. Netanyahu, C. D. Piatko, R. Silverman, A. Y. Wu: An efficient k-means clustering algorithm: Analysis and implementation. In: IEEE Trans. Pattern Analysis and Machine Intelligence. Vol. 24, 2002, S. 881–892, doi:10.1109/TPAMI.2002.1017616 (englisch, umd.edu [PDF; abgerufen am 24. April 2009]).
- ↑ C. Elkan: Using the triangle inequality to accelerate k-means. In: Proceedings of the Twentieth International Conference on Machine Learning (ICML). 2003 (ucsd.edu [PDF; 88 kB]).
- ↑ A. K. Jain, R. C. Dubes: Algorithms for Clustering Data, Prentice-Hall, 1981.
- ↑ P. S. Bradley, O. L. Mangasarian, W. N. Street: Clustering via Concave Minimization. In: M. C. Mozer, M. I. Jordan, T. Petsche (Hrsg.): Advances in Neural Information Processing Systems, vol. 9, MIT Press, Cambridge MA 1997, S. 368–374.
- ↑ T. Kanungo, D. Mount, N. Netanyahux, C. Piatko, R. Silverman, A. Wu A Local Search Approximation Algorithm for k-Means Clustering. (PDF; 170 kB) In: Computational Geometry: Theory and Applications, 2004.
- ↑ S. Vinod: Integer programming and the theory of grouping. In: Journal of the American Statistical Association. Band 64, 1969, S. 506--517.
- ↑ Module: segmentation — skimage docs. Abgerufen am 8. September 2018 (englisch).
- ↑ dlib C++ Library - kkmeans_ex.cpp. Abgerufen am 8. Januar 2019.