Kapitalmarktlinie
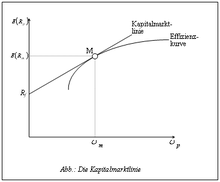
Die Kapitalmarktlinie (KML, englisch Capital Market Line, CML) ist eine Beziehung aus der Kapitalmarkttheorie. Sie ist die erwartete (i. S. von beanspruchte) Rendite-Risiko-Kombination von effizienten Portfolios im Gleichgewicht. Auf der Kapitalmarktlinie liegen alle Risiko-Rendite-Kombinationen, die der Investor bereit ist zu akzeptieren.
Die Kapitalmarktlinie ist ein Baustein des Capital Asset Pricing Model, das eine Weiterentwicklung der Portfoliotheorie ist. Es wird dabei versucht, ein Gleichgewicht zwischen mehreren Marktteilnehmern zu ermitteln, wohingegen die Portfoliotheorie nur ein repräsentatives Individuum betrachtet. Die zentrale Gleichung des CAPM, die die erwarteten Renditen durch den jeweiligen Betafaktor erklärt, ist die Wertpapierlinie.
Annahmen[Bearbeiten | Quelltext bearbeiten]
Das Konzept der Kapitalmarktlinie beruht auf folgenden Annahmen:
- Es handelt sich um risikoaverse Investoren mit möglicherweise unterschiedlichen Präferenzen.
- Die Investoren wählen nur effiziente Portfolios.
- Die Investoren haben gleiche Erwartungen aufgrund von gleichen Informationen.
- Die Investoren investieren über denselben Planungshorizont.
- Es gibt eine risikolose Anlage- und Verschuldungsmöglichkeit, wobei der Sollzins dem Habenzins entspricht.
Auf Basis dieser Annahmen lässt sich ein Gleichgewicht herleiten.
Herleitung des Gleichgewichtes[Bearbeiten | Quelltext bearbeiten]
Im individuellen Portfolio müssen im Gegensatz zum Marktportfolio nicht alle Aktien enthalten sein. Vom Tangentialportfolio hält jeder Investor einen Anteil.
Damit Markträumung auftritt, muss im Tangentialportfolio jede Aktie enthalten sein. Dies ist dann gegeben, wenn die Gesamtnachfrage und die Anzahl der umlaufenden Aktien genau gleich sind.
Die Budgetbedingung lautet
- : Anteil des Tangentialportfolios (riskanter Teil)
- : risikoloser Anteil des Portfolios
- : Anteil am Tangentialportfolio,m für jeden Investor k identisch
Markträumungsbedingung[Bearbeiten | Quelltext bearbeiten]
- : Budget des Investors
- : risikoloser Anteil des Portfolios
Budgetbedingung[Bearbeiten | Quelltext bearbeiten]
- : Summe des Budgets
- : Anlage im Tangentialportfolio
Gleichung der Kapitalmarktlinie[Bearbeiten | Quelltext bearbeiten]
- .
- Die größtmögliche Diversifikation stellt der Kauf des Marktportfolios dar. Dieses wohldiversifizierte Portfolio bietet das günstigste Risiko/Rendite-Verhältnis
- Dann ist eine Verringerung des Risikos nur noch durch Beimischung einer risikolosen Anlage möglich
- Die Steigung ist ein Quotient aus der Überrendite des Marktes und dessen Risiko . Es findet also eine Normierung statt.
Ergebnis[Bearbeiten | Quelltext bearbeiten]
- Im Gleichgewicht gilt, dass das Marktportfolio gleich dem Tangentialportfolio ist. Dies ist die einzige empirisch testbare Aussage des CAPM.
- Jeder Investor hält ein riskantes Aktienportfolio, dessen Struktur mit übereinstimmt.
- Es gilt die Tobin-Separation, d. h. die Entscheidung über den riskanten Anteil und die Entscheidung über dessen Struktur sind getrennt.
- Alle effizienten Portfolios sind vollständig positiv korreliert, da sie aus dem risikolosen Zins und dem Marktportfolio zusammengesetzt sind.













