Mengendiagramm

Mengendiagramme dienen der grafischen Veranschaulichung der Mengenlehre. Es gibt unterschiedliche Arten von Mengendiagrammen, insbesondere Euler-Diagramme (nach Leonhard Euler) und Venn-Diagramme (nach John Venn).
Mengendiagramme können Mengenbeziehungen verdeutlichen, sind jedoch im Allgemeinen nicht als mathematische Beweismittel geeignet. Als Beweismittel eignen sich nur solche Mengendiagramme, die alle möglichen Relationen der vertretenen Mengen darstellen; solche Diagramme werden Venn-Diagramme genannt. Der Nachteil von Venn-Diagrammen liegt darin, dass sie bei mehr als drei beteiligten Mengen rasch unübersichtlich werden, weil sie bei n Objekten 2n Möglichkeiten darstellen müssen. Venn selbst konnte unter der Verwendung von Ellipsen bis zu vier, schließlich sogar fünf beteiligte Mengen darstellen.
Beispiele
[Bearbeiten | Quelltext bearbeiten]Euler-Diagramme
[Bearbeiten | Quelltext bearbeiten]Euler-Diagramme werden in erster Linie dazu eingesetzt, mengentheoretische Beziehungen und Sachverhalte, zum Beispiel die Teilmengeneigenschaft, anschaulich zu machen, wobei die folgenden Veranschaulichungen üblich sind:[1]
-
; ist ein Element von .
-
; ist nicht Element von .
-
; ist eine Teilmenge von .
Weitere Beispiele für Euler-Diagramme sind:
-
Euler-Diagramm der Zahlenbereiche
-
Zugehörigkeit der europäischen und nicht europäischer Staaten zu den europäischen Institutionen
-
Euler-Diagramm der britischen Inseln
-
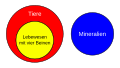
Alle Lebewesen mit vier Beinen sind Tiere, aber kein Mineral ist ein Tier.
Venn-Diagramme
[Bearbeiten | Quelltext bearbeiten]Anders als Euler-Diagramme beziehen Venn-Diagramme alle möglichen Relationen zwischen den betrachteten Mengen, also auch solche, die leer sind, mit in die Darstellung ein, so dass man an ihnen sowohl Zusammenhänge als auch das Fehlen von Zusammenhängen ablesen, aus dem Vorliegen oder Nicht-Vorliegen einzelner Relationen auf das Vorliegen oder Nicht-Vorliegen anderer Relationen schließen kann:
-
(Schnittmenge)
-
(Vereinigungsmenge)
-
(Differenzmenge)
-
(Komplement von A)
Erweiterung auf mehrere Mengen
[Bearbeiten | Quelltext bearbeiten]-
Venns Konstruktion mit n = 3
-
Venns Konstruktion mit n = 4
-
Venns Konstruktion mit n = 5
-
Venns Konstruktion mit n = 6
-
Venns elegante Lösung mit 4 Ellipsen
Venn-Diagramme sind vor allem in der Darstellung für drei Mengen mit Kreisen bekannt. Venn hatte jedoch den Ehrgeiz, „in sich elegante symmetrische Figuren“ zu finden, die eine größere Anzahl an Mengen darstellen, und zeigte ein Diagramm für vier Mengen in Ellipsenform. Er gab dann ein Konstruktionsverfahren an, mit dem man Venn-Diagramme für eine „beliebige“ Anzahl von Mengen darstellen kann, wobei jede geschlossene Kurve mit den anderen verflochten ist, ausgehend vom Diagramm mit drei Kreisen. Dabei wird ein „Schlauch“ über die jeweils letzte Mengendarstellung gezogen. Damit werden alle anderen Mengen geschnitten.
Unterschiede zwischen Venn- und Eulerdiagrammen
[Bearbeiten | Quelltext bearbeiten]Der Unterschied beider Mengendiagrammarten wird insbesondere dann deutlich, wenn man sich beide Diagramme für ein konkretes Beispiel anschaut. Man nehme hierzu die folgenden drei Mengen.
Das Euler- und das Venn-Diagramm dieser drei Mengen sieht folgendermaßen aus.
-
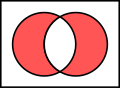
Euler-Diagramm
-
Venn-Diagramm
Während in Euler-Diagrammen nur die tatsächlichen Überschneidungen zwischen den Mengen zu sehen sind, werden in Venn-Diagrammen alle möglichen Überlappungen der Flächen dargestellt (auch wenn diese keine Objekte enthalten).
Johnston-Diagramme
[Bearbeiten | Quelltext bearbeiten]Johnston-Diagramme sind eine zweiwertige aussagenlogische Interpretation von Mengendiagrammen, speziell Venn-Diagrammen. In einem Johnston-Diagramm wird ein Kreis (eine Menge) P als Menge der Sachverhalte interpretiert, unter denen eine Aussage P wahr ist. Der Bereich außerhalb des Kreises (das Komplement der Menge) P wird als Menge der Sachverhalte interpretiert, unter denen die Aussage falsch ist. Um zu sagen, dass eine Aussage wahr ist, malt man den ganzen Bereich außerhalb ihres Kreises schwarz an; man zeigt so an, dass die Sachverhalte, unter denen die Aussage nicht wahr ist, nicht zutreffen können. Um umgekehrt zu sagen, dass eine Aussage falsch ist, malt man den Bereich innerhalb ihres Kreises schwarz aus; man sagt so, dass die Sachverhalte, unter denen die Aussage wahr ist, nicht zutreffen können. Kombiniert man zwei Aussagen P, Q durch eine Konjunktion, d. h. will man ausdrücken, dass beide Aussagen wahr sind, malt man die gesamte Fläche, die außerhalb der Schnittfläche der Kreise P, Q liegt, schwarz an; man sagt so, dass keiner der Sachverhalte, unter denen nicht sowohl P als auch Q zutreffen, vorliegen kann.
Johnston-Diagramme sind somit eine Abbildung der klassischen Aussagenlogik auf die elementare Mengenlehre, wobei die Negation als Komplementbildung, die Konjunktion als Schnitt und die Disjunktion als Vereinigung dargestellt werden. Die Wahrheitswerte wahr und falsch werden auf die Allmenge beziehungsweise auf die leere Menge abgebildet.
Geschichte
[Bearbeiten | Quelltext bearbeiten]Leibniz benutzte bereits um 1690 Mengendiagramme zur Darstellung der Syllogistik.[2] Christian Weise, Rektor des Gymnasiums in Zittau, verwendet um 1700 Mengendiagramme zur Darstellung logischer Verknüpfungen.[3] Johann Christian Lange veröffentlichte 1712 das Buch Nucleus Logicae Weisianae, in dem Weises Logik behandelt wird.[3] Leonhard Euler, Schweizer Mathematiker im 18. Jahrhundert, führte das Euler-Diagramm ein, das er erstmals in einem Brief vom 24. Februar 1761 verwendete.[4]
John Venn, britischer Mathematiker im 19. Jahrhundert, führte 1881 das Venn-Diagramm ein. 1964 werden erstmals Arbeiten von Charles Sanders Peirce akademisch gewürdigt, die dieser im letzten Viertel des 19. Jahrhunderts verfasst hatte und die die Existentiellen Graphen beschreiben.
- Anwendungsbeispiel Syllogistik
Die folgenden Grafiken zeigen, wie Venn-Diagramme seit dem 17. Jahrhundert zur Veranschaulichung von Syllogismen genutzt werden. Die Gültigkeit eines Schlusses kann mit dieser Methode überprüft werden. So sieht man etwa, dass der Modus Darapti (s. u.) nur unter der Voraussetzung eines nichtleeren Mittelbegriffs gültig ist.
In schwarzen Bereichen existiert dabei kein Element (Allaussage), in roten Bereichen zumindest ein Element x (Existenzaussage):
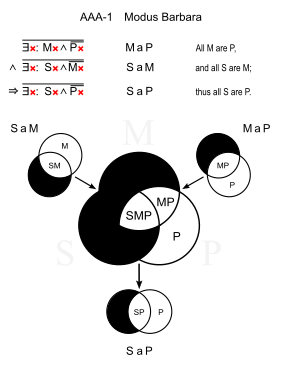 Es gibt keine M außerhalb von P, es gibt keine S außerhalb von M; also gibt es keine S außerhalb von P. |
 Es gibt keine M außerhalb von P und außerhalb von S, und es gibt einige M; also gibt es einige S in P. |
Solche Venn-Diagramme lassen sich einfach in Euler-Diagramme umformen, wie die folgende Grafik zeigt. Venn-Diagramme haben den Vorteil, dass man keine Überschneidung vergessen kann, so dass sie auch für Beweise geeignet sind. Dagegen lässt sich bei Euler-Diagrammen intuitiver erfassen, welche Mengen ineinander liegen oder sich überschneiden.

Weblinks
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Gereon Wolters: Venn-Diagramme, in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. 2. Auflage. Band 8: Th – Z. Stuttgart, Metzler 2018, ISBN 978-3-476-02107-6, S. 280 f. (mit Literaturverzeichnis).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Peter Bernhard: Euler-Diagramme. Zur Morphologie einer Repräsentationsform in der Logik. 1. Auflage. mentis Verlag, Paderborn 2001, ISBN 3-89785-142-3.
- ↑ De Formae Logicae per linearum ductus. ≈1690, erst posthum 1903 veröffentlicht in: Couturat: Opuscules et fragmentes inedits de Leibniz. S. 292–321
- ↑ a b Moritz Wilhelm Drobisch: Logik nach ihren einfachsten Verhältnissen. 5. Auflage. Verlag Leopold Voss, Hamburg Leipzig 1887 S. 99
- ↑ begriffslogik.de, abgerufen am 30. August 2008