Zweitafelprojektion
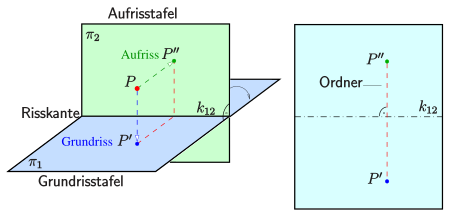
Die Zweitafelprojektion ist eine grundlegende Methode der Darstellenden Geometrie. Dabei wird ein Punkt des Anschauungsraums mit Hilfe zweier senkrechter Parallelprojektionen auf zwei zueinander senkrechte Ebenen (Bildtafel) projiziert. Üblicherweise ist die Ebene horizontal und heißt Grundrisstafel und vertikal, die Aufrisstafel. Die Schnittgerade heißt Risskante. Die entstehenden Bilder sind Grundriss bzw. Aufriss von .
Stellt man sich als x-y-Ebene und als y-z-Ebene vor, die sich in der y-Achse schneiden, so erkennt man, dass in beiden Projektionen (Rissen) alle räumlichen Informationen (Koordinaten) des Punktes enthalten sind.
Die Erweiterung der Zweitafelprojektion um eine weitere Darstellungsebene führt zur Dreitafelprojektion.
Solche Risse waren schon den Griechen und Römern bekannt. Allerdings erst eine Idee von Gaspard Monge[1] machte es möglich, die wesentlichen raumgeometrischen Probleme der darstellenden Geometrie relativ einfach zeichnerisch zu lösen. Monge klappte die Aufrisstafel um die Risskante in die Grundrisstafel und benutzte die Grundrisstafel als Zeichenebene. Die zunächst räumliche Zuordnung von und geht dabei in die Zuordnung in der Zeichenebene durch einen Ordner (Lot zur Risskante) über. Man sagt, Grundriss und Aufriss sind in der Zeichenebene über den zugehörigen Ordner einander zugeordnet.
Grund- und Aufrisse verschiedener Punkte[Bearbeiten | Quelltext bearbeiten]

Da die Anschaulichkeit der Lage von Punkten in der Zweitafelprojektion deutlich geringer ist als in einem räumlich wirkenden Bild (Axonometrie), bedarf es einiger Übung, um sich die räumliche Lage eines konkreten Punktes anhand seines Grund- und Aufrisses vorzustellen. Normalerweise erwartet man, dass sich bei einer Zweitafelprojektion der Grundriss eines Punktes unterhalb und der Aufriss eines Punktes oberhalb der Risskante befindet. Wie Beispiele in dem Bild zeigen, muss das nicht der Fall sein. Allerdings ist man immer bemüht, Grund- und Aufriss eines Objektes in der Zweitafelprojektion optisch zu trennen (Grundriss „unten“, Aufriss „oben“).
Geraden[Bearbeiten | Quelltext bearbeiten]



Eine Gerade ist durch zwei Punkte eindeutig bestimmt. Also sind ihr Grund- und Aufriss durch die Grund- und Aufrisse zweier Punkte bestimmt.
Höhenlinien, Frontlinien[Bearbeiten | Quelltext bearbeiten]
Es gibt mehrere Sonderlagen von Geraden, die besondere Bezeichnungen erhalten (siehe die Abbildung):
- Eine Höhenlinie ist eine Gerade, die parallel zur Grundrisstafel verläuft.
- Eine Frontlinie ist eine Gerade, die parallel zur Aufrisstafel verläuft.
- Eine Hauptgerade ist eine Höhen- oder Frontlinie.
- Eine Erstprojizierende ist eine Lotgerade zur Grundrisstafel und damit ein Projektionsstrahl für den Grundriss.
- Eine Zweitprojizierende ist eine Lotgerade zur Aufrisstafel und damit ein Projektionsstrahl für den Aufriss.
- Eine gelehnte Gerade ist in einer zur Risskante senkrechten Ebene enthalten. Gelehnte Geraden sind bei Konstruktionen sehr unangenehm, da sowohl Grund- und Aufriss auf den einzigen Ordner fallen (siehe die Abbildung).
Sowohl Höhen- als auch Frontlinien spielen bei der Bestimmung von wahren Längen eine besondere Rolle, denn
- eine Strecke auf einer Höhenlinie erscheint im Grundriss in wahrer Länge.
- eine Strecke auf einer Frontlinie erscheint im Aufriss in wahrer Länge.
Hauptlinien spielen auch bei rechten Winkeln eine wichtige Rolle, denn
- Ein rechter Winkel erscheint im Grundriss (Aufriss) wieder als rechter Winkel, wenn ein Schenkel auf einer Höhenlinie (Frontline) liegt.
Beliebige Winkel erscheinen im Grundriss (Aufriss) in wahrer Größe, wenn beide Schenkel parallel zur Grundrisstafel (Aufrisstafel) liegen. Tafelparallelität kann man entweder durch eine Drehung der Ebene, in der der Winkel liegt, um eine Höhenlinie (Frontlinie) oder durch zwei Umprojektionen (siehe wahre Gestalt) erreichen.
Spurpunkte[Bearbeiten | Quelltext bearbeiten]
Bei Konstruktionen werden oft die Spurpunkte einer Gerade benutzt. Sie sind die Durchstoßpunkte der Gerade mit den Risstafeln. Es gilt immer
- und
- liegen auf der Risskante (siehe Bild).
Ebenen[Bearbeiten | Quelltext bearbeiten]
Beschreibung einer Ebene, Spurgeraden[Bearbeiten | Quelltext bearbeiten]


b) Lot von Punkt auf Ebene (durch gegeben)

Eine Ebene wird in der darstellenden Geometrie in der Regel durch ein Dreieck oder zwei sich schneidende Geraden in Grund- und Aufriss beschrieben. Im zweiten Fall wählt man hierfür möglichst Hauptgeraden (Höhenlinien, Frontlinien) oder Spurgeraden (Schnittgeraden der Ebene mit den Risstafeln, siehe Bild). Auch hier bedarf es einiger Übung, um sich aus den gegebenen Grund- und Aufrissen die Lage der Ebene im Raum vorstellen zu können (siehe Bild).
Für Spurgeraden einer Ebene gilt:
- und
- fallen mit der Risskante zusammen und werden meistens weggelassen (siehe Bild).
Bei Konstruktionen mit Ebenen sind oft folgende Eigenschaften nützlich:
- Die Frontlinien einer Ebene sind alle zueinander parallel, insbesondere zur Aufrissspur (siehe Bild).
- Die Höhenlinien einer Ebene sind alle zueinander parallel, insbesondere zur Grundrissspur .
Lot auf eine Ebene, Abstand Punkt-Ebene[Bearbeiten | Quelltext bearbeiten]
Da der Riss (senkrechte Parallelprojektion) eines rechten Winkels nur dann wieder ein rechter Winkel ist, wenn ein Schenkel parallel zur Bildtafel ist (siehe Abschnitt über Geraden), gilt (siehe Bild)
- Der Grundriss eines Lotes auf eine Ebene ist senkrecht zu einer beliebigen Höhenlinie der Ebene.
- Der Aufriss eines Lotes auf eine Ebene ist senkrecht zu einer beliebigen Frontlinie der Ebene.
Will man den Abstand eines Punktes von einer Ebene bestimmen, so muss man das Lot zur Ebene durch mit der Ebene schneiden (siehe: Durchstoßpunktkonstruktion). Der Schnittpunkt ist der Lotfußpunkt . Die wahre Länge der Strecke (Lot) ist schließlich der gesuchte Abstand des Punktes von der Ebene.
Lotebene, Lot auf eine Gerade, Abstand Punkt-Gerade[Bearbeiten | Quelltext bearbeiten]
Will man das Lot von einem Punkt aus auf eine Gerade (im Raum) fällen, so verwendet man die Ebene durch , die senkrecht zu ist, als Hilfsebene. ist eine Lotebene von . Es gilt
- Der Grundriss der Höhenlinie von durch ist senkrecht zu .
- ( ist parallel zur Risskante !)
- Der Aufriss der Frontlinie von durch ist senkrecht zu .
- ( ist parallel zur Risskante !)
Damit liegt die Ebene durch die Höhen- und Frontlinie im Punkt fest. Mit Hilfe der Durchstoßpunktkonstruktion lässt sich dann der Lotfußpunkt bestimmen. Der Abstand des Punktes Q von der Gerade ist die wahre Länge der Strecke . Wie man eine wahre Länge bestimmt findet man hier.
Umprojektion, Dreitafelprojektion[Bearbeiten | Quelltext bearbeiten]


In der darstellenden Geometrie gibt es zwei Grundaufgaben, die durch Einführung eines neuen Risses gelöst werden können. Dies sei am Beispiel des Rhombendodekaeders (s. u.) erläutert. Der Rhombendodekaeder ist durch zugeordnete Risse (Grund- und Aufriss) gegeben. Gesucht ist 1) ein anschaulicher Riss (Orthogonalprojektion) und 2) die wahre Gestalt eines der 12 Rhomben.
Zunächst wird erklärt wie man einen neuen Riss eines in Grund- und Aufriss gegebenen Punktes konstruiert.
Einführung eines neuen Aufrisses[Bearbeiten | Quelltext bearbeiten]
Gegeben: Ein Punkt in Grund- und Aufriss (, Risskante ) und eine neue Aufrisstafel durch die Risskante .
Gesucht: Der neue Aufriss .
und sind also über einen Ordner (Lot zu ) einander zugeordnet. ( sind nicht einander zugeordnet !)
Aus dem Bild ist zu erkennen
- liegt auf dem Ordner (Lot zu durch ) im gleichen Abstand von wie der alte Aufriss von der alten Risskante (siehe Bild).
Beispiel Rhombendodekaeder:
In dem hier gezeigten Beispiel ist ein Rhombendodekaeder in Grund- und Aufriss gegeben.
- 1) anschaulicher Aufriss
Beide gegebenen Risse sind zwar leicht zu zeichnen, sie sind aber unanschaulich, da viele Punktepaare im Aufriss bzw. Grundriss zusammenfallen. Durch Einführen der neuen Risskante wird ein weiterer Aufriss definiert. (Die neue Risskante kann fast beliebig gewählt werden. Sie sollte nur nicht parallel und nicht senkrecht zu dem Grundriss einer der Polyederkanten sein.) In dem neuen Riss liegen keine Punkte mehr hintereinander. Dadurch sind die einzelnen Rhomben und ihre Lage im Raum besser zu erkennen. (Beim Erstellen des neuen Aufrisses lässt sich ausnutzen, dass jedes der 3 Vierecke auf gleicher Höhe liegt und damit auch den gleichen Abstand zur neuen Risskante hat.)
- 2) wahre Gestalt eines Rhombus
Offensichtlich liegt der Rhombus in einer senkrechten Ebene. Führt man eine neue Aufrissebene so ein, dass sie parallel zu dem Rhombus ist, so muss der Rhombus im neuen Riss in wahrer Gestalt erscheinen. Also wählt man eine neue Risskante parallel zu und konstruiert den neuen Aufriss der vier Punkte . Der Rhombus hat die wahre Gestalt der Rhomben.

Kreuzriss, Dreitafelprojektion[Bearbeiten | Quelltext bearbeiten]
Ist die neue Risstafel zur Grundrisstafel und zur Aufrisstafel senkrecht, d. h. , nennt man den neuen Aufriss Kreuzriss (s. Bild) und ordnet ihn direkt dem bestehenden Aufriss zu. Eine Zuordnung des neuen Risses zum Grundriss erhält man durch konzentrische Kreisbögen als Ordner (siehe Bild). Damit kann man jetzt Informationen aus irgendeinem Riss über die entsprechenden Ordner in die anderen beiden Risse übertragen. Solch eine Anordnung nennt man Dreitafelprojektion.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Rudolf Fucke, Konrad Kirch, Heinz Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4, S. 10.
- Cornelie Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X, S. 40.
- Ulrich Graf, Martin Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S. 59.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt), S. 23–34.
- Grundlagen und Elemente der Verkehrsmaschinentechnik ( vom 10. August 2013 im Internet Archive) (PDF; 493 kB) TU Dresden
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ siehe Geometrie descriptive. S. 10










































