Benutzer:Regnaron/Algorithmen-Layout
Splay Tree
[Bearbeiten | Quelltext bearbeiten]In der Informatik ist ein Spay Baum eine baumartige Datenstruktur zum verwalten verschiedener Elemente. Die Besonderheit von Splay Bäumen ist, dass sie immer balanciert sind, wodurch alle wichtigen Operationen wie einfügen, suchen und löschen effizient ausgeführt werden können. Splay Bäume wurden 1985 von Daniel Sleator and Robert Tarjan unter dem Namen Self-Adjusting Binary Search Trees vorgestellt.
Operationen
[Bearbeiten | Quelltext bearbeiten]Splay Bäume haben gegenüber normalen Bäumen eine besondere Operation splay, mittels welcher alle anderen Operationen sehr leicht durchgeführt werden können.
Splay
[Bearbeiten | Quelltext bearbeiten]Wird die Splay Operation auf ein Element x in einem Baum T angewendet, so sorgt sie dafür, dass x nach der Operation in der Wurzel von T steht. Dies wird erreicht indem das Element Schritt für Schritt im Baum hinaufrotiert wird, bis es schließlich bei der Wurzel angekommen ist. Hierzu wird x jeweils mit seinem Vater bzw. Großvater verglichen und aufgrund dieses Vergleiches werden drei Fälle unterschieden:
Bemerkung: Es wird angenommen, dass x jeweils im linken Teilbaum seines Vaters liegt. Die Fälle in denen es sich im rechten Teilbaum seines Vaters befindet sind analog.
Zick Rotation
Falls x keinen Großvater hat, und somit bereits direkt unter der Wurzel steht, wird eine zick Rotation durchgeführt. Nun ist x die neue Wurzel des Baumes und die Splay Operation beendet.
Zick-Zick Rotation
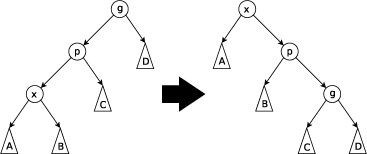
Hat x sowohl einen Vater als auch einen Großvater und ist das linke Kind des Großvaters, wird eine zick-zick Rotation durchgeführt. Hierbei wird x mit dem Großvater vertauscht, und alle weiteren Unterbäume werden an die entsprechenden Stellen gesetzt. Falls x nach der Rotation noch nicht in der Wurzel des Baumes steht, so wird weiterrotiert.
Zick-Zack Rotation
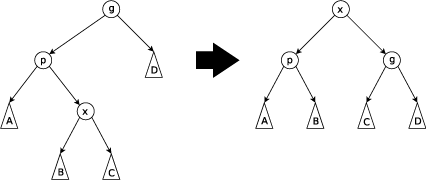
Ist x das rechte Kind seines Großvaters, so wird eine zick-zack Rotation durchgeführt. Hierbei tauscht x die Position mit seinem Großvater und alle weiteren Unterbäume werden an die entsprechenden Stellen gesetzt. Falls x nach der Rotation noch nicht in der Wurzel des Baumes steht, so wird weiterrotiert.
Amortisierte Laufzeit: O(log n)
Suchen
[Bearbeiten | Quelltext bearbeiten]Um ein Element x im Baum T zu suchen, führt man einfach splay(x,T) aus. Dies bewirkt, dass falls x in T enthalten war, es nun in der Wurzel steht. Somit muss man nur noch die neue Wurzel mit x vergleichen. Sind sie unterschiedlich, war x nicht im Baum.
Amortisierte Laufzeit: O(log n)
Einfügen
[Bearbeiten | Quelltext bearbeiten]Um ein Element x in einen Splay Baum T einzufügen, macht man zuerst einmal den Nachfolger bzw Vorgänger von x mittels splay(x,T) im Baum zur Wurzel. Nun kann man diese Wurzel y mit x vergleichen. Gilt x < y, so macht man den linken Teilbaum von y zum linken Teilbaum von x. Da alle Elemente im linken Teilbaum von y kleiner als y selbst waren, und y kleiner als x ist, geht dies ohne Probleme. Sollte x größer als y sein, so macht man analog den rechten Teilbaum von y zum rechten Kind von x, und macht y samt seines linken Teilbaumes zum linken Kind von x.
Amortisierte Laufzeit: O(log n)
Löschen
[Bearbeiten | Quelltext bearbeiten]Um x aus T zu löschen, macht man das Element mittels splay(x, T) zur Wurzel von T, und löscht es dann. Nun bekommt man eventuell zwei Splay Bäume, welche man mittels join wieder zu einem Splay Baum vereinigen kann.
Amortisierte Laufzeit: O(log n)
Vereinigen
[Bearbeiten | Quelltext bearbeiten]Die Operation merge wiedervereinigt zwei Splay Bäume T1 und T2 welche unmittelbar vorher mittels split getrennt wurden. Hierbei wird zuerst mittels splay(∞,T1) das maximale Element x1 des ersten Baumes gesucht und in die Wurzel rotiert. Da die beiden Bäume T1 und T2 das Ergebnis einer vorherigen split Operation sind, sind alle Elemente in T2 größer als die Elemente in T1, weswegen man den Baum T2 nun ohne Probleme zum rechten Kind von x1 machen kann.
Amortisierte Laufzeit: O(log n)
Aufsplitten
[Bearbeiten | Quelltext bearbeiten]Um einen Splay Baum T bei dem Knoten x in zwei Splay Bäume aufzusplitten, macht man zuerst x mittels splay zur Wurzel von T. War x im Baum enthalten, kann man nun die Verbindung zu einem der beiden Teilbäume einfach trennen. Steht nach der Splay Operation ein anderes Element y in der Wurzel, so war x selbst nicht in T enthalten. Ist x nun kleiner als y, so kann man das linke Kind von y abschneiden, andernfalls sein rechtes.
Amortisierte Laufzeit: O(log n)