Kan-Komplex
Zur Navigation springen
Zur Suche springen
In der Algebraischen Topologie, einem Teilgebiet der Mathematik, sind Kan-Komplexe ein Hilfsmittel zur kombinatorischen Definition von Homotopiegruppen.
Definition[Bearbeiten | Quelltext bearbeiten]
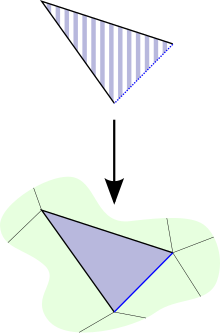
Eine simpliziale Menge ist ein Kan-Komplex, wenn sie die Kan-Erweiterungs-Eigenschaft erfüllt:
- Für alle und jede -elementige Menge von -Simplizes mit für alle gibt es ein -Simplex mit für .
Homotopiegruppen[Bearbeiten | Quelltext bearbeiten]
D. M. Kan[1] gab eine kombinatorische Definition von Homotopiegruppen für Kan-Komplexe.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Sei ein topologischer Raum. Die singuläre simpliziale Menge sei wie folgt definiert. Die -Simplizes in sind die stetigen Abbildungen des Standard--Simplexes nach . Die Randabbildungen von werden von den Randabbildungen induziert.
ist ein Kan-Komplex, seine Homotopiegruppen (im Sinne von Kan) stimmen mit den Homotopiegruppen von überein.
Literatur[Bearbeiten | Quelltext bearbeiten]
- J. Peter May: Simplicial objects in algebraic topology. Reprint of the 1967 original. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL 1992, ISBN 0-226-51181-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Daniel Marinus Kan: A combinatorial definition of homotopy groups. In: Ann. of Math. (2) 67 1958, S. 282–312.














