Das Lemma von Arden trifft eine Aussage über Mengen von Zeichenreihen, welche im Rahmen der formalen Sprachen Gegenstand der theoretischen Informatik, spezieller der Automatentheorie sind.
Es sei  ein beliebiges Alphabet;
ein beliebiges Alphabet;  stehe für den Kleene-Stern,
stehe für den Kleene-Stern,  für die positive transitive Hülle,
für die positive transitive Hülle,  für die Konkatenation zweier Zeichenreihen-Mengen und
für die Konkatenation zweier Zeichenreihen-Mengen und  für deren gewöhnliche Vereinigung (in dieser Priorität – Klammerung wird entsprechend vernachlässigt). Dann gilt folgende Äquivalenz:
für deren gewöhnliche Vereinigung (in dieser Priorität – Klammerung wird entsprechend vernachlässigt). Dann gilt folgende Äquivalenz:

bzw. folgende Gleichung:

In Worten: Für eine beliebige Zeichenreihen-Menge  und eine Zeichenreihen-Menge
und eine Zeichenreihen-Menge  , welche das leere Wort
, welche das leere Wort  nicht enthält, hat die Gleichung
nicht enthält, hat die Gleichung  nur die eine Lösung
nur die eine Lösung  .
.
Auf die Quantisierung sei in beiden Beweisteilen der besseren Lesbarkeit halber weg verzichtet, was bei Allquantifizierung nicht weiter problematisch ist, solange keine Spezifikationen für die betreffenden Variablen vorgenommen werden. Entsprechende Stellen werden speziell behandelt.
Es sei  eine Lösung für
eine Lösung für  in der Gleichung
in der Gleichung  .
.
Zunächst wird die Definition des Kleene-Sternes angewendet und die Distributivität der Konkatenation über Vereinigungen genutzt:

Nun lässt sich durch vollständige Induktion über  zeigen, dass
zeigen, dass  für alle
für alle  gilt:
gilt:



Da für verschiedene n alle  paarweise disjunkt sind, folgt aus
paarweise disjunkt sind, folgt aus  auch die ursprüngliche Obermengen-Beziehung
auch die ursprüngliche Obermengen-Beziehung  .
.
Hier wird der Beweis indirekt geführt: Man nimmt an,  gilt nicht, womit es mindestens ein Wort
gilt nicht, womit es mindestens ein Wort  mit
mit  geben muss. Weil
geben muss. Weil  ist, muss
ist, muss  auch Element von
auch Element von  sein oder anders formuliert
sein oder anders formuliert  .
Im ersten Fall setzt sich
.
Im ersten Fall setzt sich  aus zwei Teilwörtern
aus zwei Teilwörtern  und
und  zusammen, also
zusammen, also  . Da
. Da  nicht das leere Wort sein kann (die Quantifizierung fordert
nicht das leere Wort sein kann (die Quantifizierung fordert  ), folgt
), folgt  . Betrachtet man das kleinste der als existierenden angenommenen
. Betrachtet man das kleinste der als existierenden angenommenen  , dann müsste außerdem
, dann müsste außerdem  gelten, was aber im Widerspruch zur Annahme
gelten, was aber im Widerspruch zur Annahme  steht. Im anderen Fall, also
steht. Im anderen Fall, also  , ergibt sich ebenfalls der Widerspruch
, ergibt sich ebenfalls der Widerspruch  . Da beide Fälle in Widersprüchen enden, muss die Annahme falsch gewesen sein, dass
. Da beide Fälle in Widersprüchen enden, muss die Annahme falsch gewesen sein, dass  nicht gilt.
nicht gilt.
Diese Beweisrichtung ist trivial, da es reicht zu zeigen, dass  die Gleichung
die Gleichung  überhaupt löst:
überhaupt löst:

Die zentrale Bedeutung des Arden-Lemmas ist seine Anwendung in der Automatentheorie. Es erleichtert das Ermitteln der mengentechnischen Beschreibung, der von einem Nichtdeterministischen endlichen Automaten (NEA) akzeptierten Sprache:
Betrachtet wird ein NEA  , dessen Zustände mit den natürlichen Zahlen von
, dessen Zustände mit den natürlichen Zahlen von  bis
bis  bezeichnet sein sollen (also
bezeichnet sein sollen (also  ). Zusätzlich werden folgende Definitionen herangezogen:
). Zusätzlich werden folgende Definitionen herangezogen:


Mit Hilfe dieser Mengen lässt sich die Teilsprache jedes Zustands  angeben:
angeben:

Durch die Definition von  erhält man ein Gleichungs-System mit
erhält man ein Gleichungs-System mit  Gleichungen:
Gleichungen:

Nun bringt man eine Teilsprache auf eine geeignete Form, welche eine Anwendung des Lemmas ermöglicht:

Laut Arden’s Lemma ist diese Aussage äquivalent zu folgender:

Diese Lösung ist eindeutig. Setzt man nun  in alle anderen Gleichungen ein, so erhält man ein Gleichungs-System mit einer Variable weniger und kann so auf diese Weise immer weiter bis zum trivialen Fall vereinfachen, bei dem nur noch eine Gleichung übrig ist, welche man unabhängig von allen anderen Teilsprachen lösen kann. Durch Rückwärts-Einsetzen erhält man dann auch die übrigen Teilsprachen um schlussendlich die eindeutige Lösung des gesamten Gleichungs-Systems zu ermitteln und mit
in alle anderen Gleichungen ein, so erhält man ein Gleichungs-System mit einer Variable weniger und kann so auf diese Weise immer weiter bis zum trivialen Fall vereinfachen, bei dem nur noch eine Gleichung übrig ist, welche man unabhängig von allen anderen Teilsprachen lösen kann. Durch Rückwärts-Einsetzen erhält man dann auch die übrigen Teilsprachen um schlussendlich die eindeutige Lösung des gesamten Gleichungs-Systems zu ermitteln und mit  die vom Automaten
die vom Automaten  akzeptierte Sprache
akzeptierte Sprache  zu identifizieren.
zu identifizieren.
Aus Sicht der abstrakten Algebra stellt  die Struktur eines Dioids dar, was heißt, dass sowohl
die Struktur eines Dioids dar, was heißt, dass sowohl  als auch
als auch  einen Monoiden bilden und
einen Monoiden bilden und  distributiv über
distributiv über  ist. Das neutrale Element bezüglich der Vereinigung ist die leere Menge und das neutrale Element bezüglich der Konkatenation ist
ist. Das neutrale Element bezüglich der Vereinigung ist die leere Menge und das neutrale Element bezüglich der Konkatenation ist  . Aufgrund der fehlenden Invertierbarkeit ist es im Allgemeinen nicht möglich Gleichungen über dieser Struktur zu lösen. Das Lemma von Arden ermöglicht es aber zumindest die Lösungen einiger spezieller Gleichungen zu ermitteln und das sogar eindeutig.
. Aufgrund der fehlenden Invertierbarkeit ist es im Allgemeinen nicht möglich Gleichungen über dieser Struktur zu lösen. Das Lemma von Arden ermöglicht es aber zumindest die Lösungen einiger spezieller Gleichungen zu ermitteln und das sogar eindeutig.




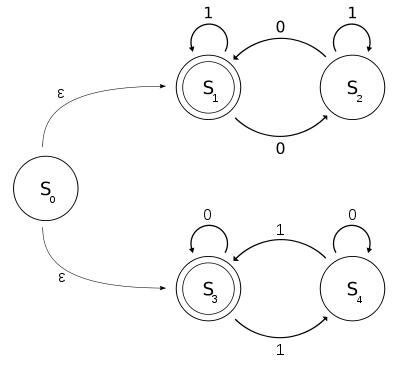
Man erhält damit das folgende Gleichungs-System:

Durch die Anwendung des Lemmas erhält man schrittweise die Lösung:









Da  der Startzustand von
der Startzustand von  ist, gilt
ist, gilt  , was der dem regulären Ausdruck
, was der dem regulären Ausdruck  zugeordneten Sprache entspricht.
zugeordneten Sprache entspricht.
- D. N. Arden: Theory of Computing Machine Design: An Intensive Course for Engineers, Scientists, and Mathematicians, University of Michigan Press, Michigan, USA, 1960 (S. 1–35)
- John E. Hopcroft: Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, 1979. ISBN 0-201-02988-X
- Marko Van Eekelen, Herman Geuvers, Julien Schmaltz, Freek Wiedijk: Interactive Theorem Proving, Springer Science & Business Media, 2011
- Harold V. McIntosh: One Dimensional Cellular Automata, Luniver Press, 2009 (S. 87)
- A. Arnold, D. Niwinski: Rudiments of µ-calculus, Elsevier, 2001 (ab S. 107)
- John Daintith: Ardens rule, Oxford University Press, 2004 (englisch)













































































