„Achsenabschnittsform“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
Quartl (Diskussion | Beiträge) K →Weitere Ebenengleichungen: link |
Quartl (Diskussion | Beiträge) überarbeitet |
||
| Zeile 1: | Zeile 1: | ||
Die '''Achsenabschnittsform''' ist in der [[Mathematik]] eine spezielle Form einer [[Geradengleichung]] oder [[Ebenengleichung]]. Bei der Achsenabschnittsform wird eine [[Gerade]] in der [[Euklidische Ebene|euklidischen Ebene]] oder eine [[Ebene (Mathematik)|Ebene]] im [[Euklidischer Raum|euklidischen Raum]] über ihre Schnittpunkte mit den [[Koordinatenachse]]n beschrieben. Diese Schnittpunkte werden auch [[Spurpunkt]]e genannt, ihre Verbindungsstrecken liegen bei einer Ebene allgemein auf den [[Spurgerade]]n und bilden das [[Spurdreieck (Vektorrechnung)|Spurdreieck]]. Bei der Achsenabschnittsform handelt sich um eine spezielle [[Implizite Funktion|implizite Darstellung]] der Gerade oder Ebene. Sie ist nicht definiert, wenn die Gerade oder Ebene durch den [[Koordinatenursprung]] verläuft. |
|||
[[bild:Ebene_Achsenabschnittsform.PNG|thumb|Achsenabschnittsform]] |
|||
Die '''Achsenabschnittsform''' einer [[Ebene (Mathematik)|Ebene]] ist eine Gleichung, die diese Ebene mittels ihrer Achsenabschnitte auf den [[Koordinatensystem|Koordinatenachsen]] ("[[Spurpunkt]]e") beschreibt. Wenn ''a'', ''b'' und ''c'' die Abschnitte auf der x-Achse, y-Achse und z-Achse sind, so lautet die Achsenabschnittsform: |
|||
== Achsenabschnittsform einer Geradengleichung == |
|||
| ⚫ | |||
| ⚫ | |||
=== Darstellung === |
|||
Anwendung findet diese Darstellung z.B. bei den [[Millersche Indizes|Millerschen Indizes]]. |
|||
In der Achsenabschnittsform wird eine Gerade <math>g</math> in der Ebene durch zwei reelle Zahlen <math>a</math> und <math>b</math> folgendermaßen über eine [[lineare Gleichung]] beschrieben: |
|||
| ⚫ | |||
:<math>g = \{ (x,y) \in \R^2 \mid \frac{x}{x_0} + \frac{y}{y_0} = 1 \}</math>. |
|||
== Erklärung == |
|||
Alle Punkte, deren Koordinaten <math>(x,y)</math> die Gleichung erfüllen, liegen auf der Gerade. Hierbei sind <math>(x_0,0)</math> und <math>(0,y_0)</math> die Schnittpunkte der Gerade mit den beiden [[Koordinatenachse]]n, die auch als [[Spurpunkt]]e bezeichnet werden. Verläuft die Gerade parallel zu einer der Koordinatenachsen, dann fällt der jeweilige Spurpunkt und damit auch der entsprechende Term in der Achsenabschnittsform weg. Die Achsenabschnittsform ist nicht definiert, wenn die Gerade durch den [[Koordinatenursprung]] verläuft. |
|||
Die Achsenabschnittsform der Ebene kann man aus der [[Normalgleichung|Normalform]] herleiten. Mit einem Normalenvektor <math> \vec n</math> gilt für jeden [[Ortsvektor]] <math>\vec r</math>, der zu einem Punkt P der Ebene gehört: |
|||
| ⚫ | |||
| ⚫ | |||
Ein Beispiel für eine Geradengleichung in Achsenabschnittsform ist |
|||
mit einer Konstanten ''k''. Die [[Spurpunkt]]e S<sub>x</sub>, S<sub>y</sub> und S<sub>z</sub> haben insbesondere die Ortsvektoren |
|||
| ⚫ | |||
:<math>\begin{pmatrix} a \\ 0 \\ 0 \end{pmatrix}</math>,<math>\begin{pmatrix} 0 \\ b \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 0 \\ 0 \\ c \end{pmatrix}</math>. |
|||
Jede Wahl von <math>(x,y)</math>, die diese Gleichung erfüllt, beispielsweise <math>(-2,1)</math> oder <math>(2,3)</math>, entspricht genau einem Geradenpunkt. Die beiden Spurpunkte der Geraden sind <math>(-4,0)</math> und <math>(0,2)</math>. |
|||
Wenn <math>\vec n = \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix}</math> ist, folgt also: |
|||
=== Berechnung === |
|||
:<math>k = \begin{pmatrix} a \\ 0 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} 0 \\ b \\ 0 \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ c \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix}</math>, |
|||
| ⚫ | |||
d. h. |
|||
Aus der [[Koordinatenform#Koordinatenform einer Geradengleichung|Koordinatenform einer Geradengleichung]] mit den Parametern <math>a, b</math> und <math>c</math> lassen sich die Parameter der Achsenabschittsform mittels Division durch <math>c</math> direkt angeben: |
|||
:<math> k = a \cdot n_x = b \cdot n_y = c \cdot n_z</math> |
|||
:<math>x_0 = \frac{a}{c}, ~ y_0 = \frac{b}{c}</math>. |
|||
und daher |
|||
==== Aus der Normalenform ==== |
|||
:<math>{1 \over a} = {n_x \over k}</math>, <math>{1 \over b} = {n_y \over k}</math> und <math>{1 \over c} = {n_z \over k}</math>. |
|||
Aus der [[Normalenform#Normalenform einer Geradengleichung|Normalenform einer Geradengleichung]] mit Stützvektor <math>\vec p</math> und Normalenvektor <math>\vec n</math> lassen sich die Parameter der Achsenabschnittsform durch Ausmultiplizieren der Normalengleichung und anschließende Division durch den konstanten Term ablesen: |
|||
Indem man nun die Normalform |
|||
:<math> |
:<math>x_0 = \frac{n_1}{c}, ~ y_0 = \frac{n_2}{c}</math> mit <math>c = p_1 n_1 + p_2 n_2</math>. |
||
Liegt eine Gerade in [[Hessesche Normalform|hessescher Normalform]] vor, so entspricht der konstante Term <math>c</math> gerade dem Abstand der Gerade vom Koordinatenursprung. |
|||
durch ''k'' dividiert, erhält man |
|||
==== Aus der Parameterform ==== |
|||
:<math>\begin{pmatrix} x \\ y \\ z \end{pmatrix} \cdot \begin{pmatrix} {n_x \over k} \\ {n_y \over k} \\ {n_z \over k} \end{pmatrix} = 1 </math>, |
|||
Aus der [[Parameterform#Parameterform einer Geradengleichung|Parameterform einer Geradengleichung]] mit Stützvektor <math>\vec p</math> und Richtungsvektor <math>\vec u</math> wird zunächst ein Normalenvektor der Geraden über <math>\vec n = ( -u_2, u_1 )</math> bestimmt und daraus dann die Parameter der Geraden in der Achsenabschnittsform wie bei der Normalenform. Analog lässt sich auf diese Weise auch aus der [[Zweipunkteform]] einer Geradengleichung ein Normalenvektor ermitteln und daraus dann die Achsenabschnittsform. |
|||
ausmultipliziert: |
|||
== Achsenabschnittsform einer Ebenengleichung == |
|||
:<math>x \cdot {n_x \over k} + y \cdot {n_y \over k} + z \cdot {n_z \over k} = 1</math>, |
|||
[[Datei:Plane equation qtl5.svg|miniatur|Achsenabschnittsform einer Ebenengleichung]] |
|||
=== Darstellung === |
|||
und folglich die Achsenabschnittsform: |
|||
Analog wird eine Ebene <math>E</math> im dreidimensionalen Raum in der Achsenabschnittsform durch drei reelle Zahlen <math>x_0</math>, <math>y_0</math> und <math>z_0</math> beschrieben: |
|||
| ⚫ | |||
:<math>E = \{ (x,y,z) \in \R^3 \mid \frac{x}{x_0} + \frac{y}{y_0} + \frac{z}{z_0} = 1 \}</math>. |
|||
== Ausnahmen und Sonderfälle == |
|||
Alle Punkte, deren Koordinaten <math>(x,y,z)</math> die Gleichung erfüllen, liegen auf der Ebene. Hierbei sind <math>(x_0,0,0)</math>, <math>(0,y_0,0)</math> und <math>(0,0,z_0)</math> die Schnittpunkte der Ebene mit den Koordinatenachsen. Diese Achsenabschnitte werden wiederum Spurpunkte genannt, ihre Verbindungsstrecken liegen im Allgemeinfall auf den [[Spurgerade]]n und bilden das [[Spurdreieck (Vektorrechnung)|Spurdreieck]]. Verläuft die Ebene parallel zu einer oder zwei Koordinatenachsen, dann fallen die jeweiligen Spurpunkte und damit auch die entsprechenden Terme in der Achsenabschnittsform weg. Die Achsenabschnittsform ist nicht definiert, wenn die Ebene durch den Koordinatenursprung verläuft. |
|||
Die Achsenabschnittsform existiert ''nicht'', falls die Ebene durch den Koordinatenursprung verläuft. In diesem Falle sind alle Achsenabschnitte 0, und in der Normalform wird ''k'' = 0. |
|||
[[Division durch null]] ist nicht erlaubt / nicht möglich. |
|||
=== Beispiel === |
|||
Verläuft die Ebene [[Parallel (Geometrie)|parallel]] zu einer oder zu zwei Koordinatenachsen, so fallen ein oder zwei Spurpunkte weg. Damit fällt auch der betreffende Term in der Achsenabschnittsform weg. Eine Ebene, die parallel zur y-Achse verläuft, hat z. B. keinen Achsenabschnitt ''b''; es verbleibt nur |
|||
Ein Beispiel für eine Ebenengleichung in Achsenabschnittsform ist |
|||
:<math>{x \over a} + {z \over c} = 1</math>. |
|||
| ⚫ | |||
| ⚫ | |||
Jede Wahl von <math>(x,y,z)</math>, die diese Gleichung erfüllt, beispielsweise <math>(2,0,1)</math> oder <math>(4,3,2)</math>, entspricht genau einem Ebenenpunkt. Die drei Spurpunkte der Ebene sind <math>(2,0,0)</math>, <math>(0,3,0)</math> und <math>(0,0,-1)</math>. |
|||
Eine Ebene hat den Normalenvektor |
|||
=== Berechnung === |
|||
:<math>\vec n = \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix}</math> |
|||
==== Aus der Koordinatenform ==== |
|||
und verläuft durch den Punkt P(3|2|1). Ihre Normalform lautet also: |
|||
Aus der [[Koordinatenform#Koordinatenform einer Ebenengleichung|Koordinatenform einer Ebenengleichung]] mit den Parametern <math>a, b, c</math> und <math>d</math> lassen sich die Parameter der Achsenabschittsform mittels Division durch <math>d</math> direkt angeben: |
|||
:<math>\vec r \cdot \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix} = 4 \cdot 3 - 3 \cdot 2 + 6 \cdot 1 = 12</math>. |
|||
:<math>x_0 = \frac{a}{d}, ~ y_0 = \frac{b}{d}, ~ z_0 = \frac{c}{d}</math>. |
|||
Division durch 12 liefert: |
|||
==== Aus der Normalenform ==== |
|||
:<math>\vec r \cdot \begin{pmatrix} {4 \over 12} \\ {-3 \over 12}\\ {6 \over 12}\end{pmatrix} = 1</math>, |
|||
Aus der [[Normalenform#Normalenform einer Ebenengleichung|Normalenform einer Ebenengleichung]] mit Stützvektor <math>\vec p</math> und Normalenvektor <math>\vec n</math> lassen sich die Parameter der Ebene in Achsenabschnittsform durch Ausmultiplizieren der Normalengleichung und anschließende Division durch den konstanten Term ablesen: |
|||
also ergibt sich mit <math>\vec r = \begin{pmatrix} x \\ y \\ z \end{pmatrix}</math>, |
|||
:<math> |
:<math>x_0 = \frac{n_1}{d}, ~ y_0 = \frac{n_2}{d}, ~ z_0 = \frac{n_3}{d}</math> mit <math>d = p_1 n_1 + p_2 n_2 + p_3 n_3</math>. |
||
Liegt eine Ebene in [[Hessesche Normalform|hessescher Normalform]] vor, so entspricht der konstante Term <math>d</math> gerade dem Abstand der Ebene vom Koordinatenursprung. |
|||
==Weitere Ebenengleichungen== |
|||
Weitere Ebenengleichungen sind |
|||
==== Aus der Parameterform ==== |
|||
*die [[Normalgleichung|Normalform]] bzw. die [[Hessesche Normalform]] |
|||
Aus der [[Parameterform#Parameterform einer Ebenengleichung|Parameterform einer Ebenengleichung]] mit Stützvektor <math>\vec p</math> und den beiden Richtungsvektoren <math>\vec u</math> und <math>\vec v</math> wird zunächst ein Normalenvektor der Ebene über das [[Kreuzprodukt]] <math>\vec n = \vec u \times \vec v</math> bestimmt und daraus dann die Parameter der Ebene in Achsenabschnittsform wie bei der Normalenform. Analog lässt sich auf diese Weise auch aus der [[Dreipunkteform]] einer Ebenengleichung ein Normalenvektor ermitteln und daraus dann die Achsenabschnittsform. |
|||
| ⚫ | |||
== Anwendung == |
|||
Die Achsenabschnittsform wird beispielsweise in der [[Kristallographie]] bei den [[Millersche Indizes|Millerschen Indizes]] zur Bezeichnung von Kristallflächen verwendet. |
|||
== Literatur == |
|||
* {{Literatur|Autor=Steffen Goebbels, Stefan Ritter|Titel=Mathematik verstehen und anwenden|Verlag=Springer|Jahr=2011|ISBN=978-3-827-42762-5}} |
|||
[[Kategorie:Analytische Geometrie]] |
[[Kategorie:Analytische Geometrie]] |
||
Version vom 25. Februar 2014, 09:39 Uhr
Die Achsenabschnittsform ist in der Mathematik eine spezielle Form einer Geradengleichung oder Ebenengleichung. Bei der Achsenabschnittsform wird eine Gerade in der euklidischen Ebene oder eine Ebene im euklidischen Raum über ihre Schnittpunkte mit den Koordinatenachsen beschrieben. Diese Schnittpunkte werden auch Spurpunkte genannt, ihre Verbindungsstrecken liegen bei einer Ebene allgemein auf den Spurgeraden und bilden das Spurdreieck. Bei der Achsenabschnittsform handelt sich um eine spezielle implizite Darstellung der Gerade oder Ebene. Sie ist nicht definiert, wenn die Gerade oder Ebene durch den Koordinatenursprung verläuft.
Achsenabschnittsform einer Geradengleichung

Darstellung
In der Achsenabschnittsform wird eine Gerade in der Ebene durch zwei reelle Zahlen und folgendermaßen über eine lineare Gleichung beschrieben:
- .
Alle Punkte, deren Koordinaten die Gleichung erfüllen, liegen auf der Gerade. Hierbei sind und die Schnittpunkte der Gerade mit den beiden Koordinatenachsen, die auch als Spurpunkte bezeichnet werden. Verläuft die Gerade parallel zu einer der Koordinatenachsen, dann fällt der jeweilige Spurpunkt und damit auch der entsprechende Term in der Achsenabschnittsform weg. Die Achsenabschnittsform ist nicht definiert, wenn die Gerade durch den Koordinatenursprung verläuft.
Beispiel
Ein Beispiel für eine Geradengleichung in Achsenabschnittsform ist
Jede Wahl von , die diese Gleichung erfüllt, beispielsweise oder , entspricht genau einem Geradenpunkt. Die beiden Spurpunkte der Geraden sind und .
Berechnung
Aus der Koordinatenform
Aus der Koordinatenform einer Geradengleichung mit den Parametern und lassen sich die Parameter der Achsenabschittsform mittels Division durch direkt angeben:
- .
Aus der Normalenform
Aus der Normalenform einer Geradengleichung mit Stützvektor und Normalenvektor lassen sich die Parameter der Achsenabschnittsform durch Ausmultiplizieren der Normalengleichung und anschließende Division durch den konstanten Term ablesen:
- mit .
Liegt eine Gerade in hessescher Normalform vor, so entspricht der konstante Term gerade dem Abstand der Gerade vom Koordinatenursprung.
Aus der Parameterform
Aus der Parameterform einer Geradengleichung mit Stützvektor und Richtungsvektor wird zunächst ein Normalenvektor der Geraden über bestimmt und daraus dann die Parameter der Geraden in der Achsenabschnittsform wie bei der Normalenform. Analog lässt sich auf diese Weise auch aus der Zweipunkteform einer Geradengleichung ein Normalenvektor ermitteln und daraus dann die Achsenabschnittsform.
Achsenabschnittsform einer Ebenengleichung
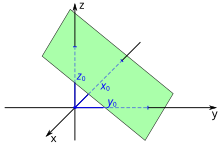
Darstellung
Analog wird eine Ebene im dreidimensionalen Raum in der Achsenabschnittsform durch drei reelle Zahlen , und beschrieben:
- .
Alle Punkte, deren Koordinaten die Gleichung erfüllen, liegen auf der Ebene. Hierbei sind , und die Schnittpunkte der Ebene mit den Koordinatenachsen. Diese Achsenabschnitte werden wiederum Spurpunkte genannt, ihre Verbindungsstrecken liegen im Allgemeinfall auf den Spurgeraden und bilden das Spurdreieck. Verläuft die Ebene parallel zu einer oder zwei Koordinatenachsen, dann fallen die jeweiligen Spurpunkte und damit auch die entsprechenden Terme in der Achsenabschnittsform weg. Die Achsenabschnittsform ist nicht definiert, wenn die Ebene durch den Koordinatenursprung verläuft.
Beispiel
Ein Beispiel für eine Ebenengleichung in Achsenabschnittsform ist
Jede Wahl von , die diese Gleichung erfüllt, beispielsweise oder , entspricht genau einem Ebenenpunkt. Die drei Spurpunkte der Ebene sind , und .
Berechnung
Aus der Koordinatenform
Aus der Koordinatenform einer Ebenengleichung mit den Parametern und lassen sich die Parameter der Achsenabschittsform mittels Division durch direkt angeben:
- .
Aus der Normalenform
Aus der Normalenform einer Ebenengleichung mit Stützvektor und Normalenvektor lassen sich die Parameter der Ebene in Achsenabschnittsform durch Ausmultiplizieren der Normalengleichung und anschließende Division durch den konstanten Term ablesen:
- mit .
Liegt eine Ebene in hessescher Normalform vor, so entspricht der konstante Term gerade dem Abstand der Ebene vom Koordinatenursprung.
Aus der Parameterform
Aus der Parameterform einer Ebenengleichung mit Stützvektor und den beiden Richtungsvektoren und wird zunächst ein Normalenvektor der Ebene über das Kreuzprodukt bestimmt und daraus dann die Parameter der Ebene in Achsenabschnittsform wie bei der Normalenform. Analog lässt sich auf diese Weise auch aus der Dreipunkteform einer Ebenengleichung ein Normalenvektor ermitteln und daraus dann die Achsenabschnittsform.
Anwendung
Die Achsenabschnittsform wird beispielsweise in der Kristallographie bei den Millerschen Indizes zur Bezeichnung von Kristallflächen verwendet.
Literatur
- Steffen Goebbels, Stefan Ritter: Mathematik verstehen und anwenden. Springer, 2011, ISBN 978-3-8274-2762-5.










































