Kreuzprodukt

Kreuzprodukt

Das Kreuzprodukt (auch Vektorprodukt, vektorielles Produkt oder äußeres Produkt genannt) ist eine Verknüpfung im euklidischen Vektorraum, die im dreidimensionalen Fall zwei Vektoren wieder einen Vektor zuordnet. Um es von anderen Produkten, insbesondere vom Skalarprodukt, zu unterscheiden, wird es mit einem Malkreuz als Multiplikationszeichen geschrieben.

Das Kreuzprodukt der Vektoren $\vec a$ und $\vec b$ ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit ihnen ein Rechtssystem bildet. Die Länge dieses Vektors entspricht dem Flächeninhalt des Parallelogramms, das von den Vektoren $\vec a$ und $\vec b$ aufgespannt wird.

In der Physik tritt das Kreuzprodukt beispielsweise bei der Berechnung der Lorentzkraft sowie in diversen Drehgrößen wie Drehmoment, Drehimpuls, Corioliskraft usw. auf.

Geometrische Definition

Rechte-Hand-Regel

Das Kreuzprodukt $\vec{a}\times\vec{b}$ von zwei Vektoren $\vec a$ und $\vec b$ im dreidimensionalen Anschauungsraum ist ein Vektor, der orthogonal zu $\vec a$ und $\vec b$, und damit zu der von $\vec a$ und $\vec b$ aufgespannten Ebene ist.

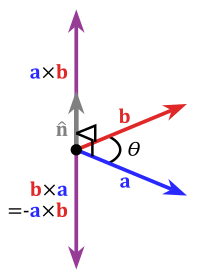
Dieser Vektor ist so orientiert, dass $\vec a, \vec b$ und $\vec{a}\times\vec{b}$ in dieser Reihenfolge ein Rechtssystem bilden, das heißt, $\vec a, \vec b$ und $\vec{a}\times\vec{b}$ verhalten sich wie Daumen, Zeigefinger und abgespreizter Mittelfinger der rechten Hand (Rechte-Hand-Regel).

Der Betrag von $\vec{a}\times\vec{b}$ gibt den Flächeninhalt des von $\vec a$ und $\vec b$ aufgespannten Parallelogramms an. Ausgedrückt durch den von $\vec a$ und $\vec b$ eingeschlossenen Winkel $\theta$ gilt

$|\vec{a}\times\vec{b}| = |\vec{a}|\, |\vec{b}|\, \sin\theta \,.$

Dabei bezeichnen $\vert\vec{a}\vert$ und $\vert\vec{b}\vert$ die Längen der Vektoren $\vec{a}$ und $\vec{b}$, und $\sin \theta\,$ ist der Sinus des von ihnen eingeschlossenen Winkels $\theta$.

Zusammenfassend gilt also

$\vec{a}\times\vec{b} = (|\vec{a}|\, |\vec{b}|\, \sin\theta) \, \vec{n}\,,$

wobei der Vektor $\vec{n}$ derjenige zu $\vec{a}$ und $\vec{b}$ senkrechte Einheitsvektor ist, der diese zu einem Rechtssystem ergänzt.

Begriff und Schreibweisen

In verschiedenen Ländern sind für das Vektorprodukt zum Teil verschiedene Schreibweisen gebräuchlich. Im englisch- und deutschsprachigen Raum wird für das Vektorprodukt zweier Vektoren $\vec{a}$ und $\vec{b}$ für gewöhnlich die Schreibweise $\vec{a}\times\vec{b}$ verwendet, in Frankreich wird dagegen die Schreibweise $\vec{a}\wedge\vec{b}$ bevorzugt. In Russland wird das Vektorprodukt oft in der Schreibweise $\left[\vec{a}\ \vec{b}\right]$ oder $\left[\vec{a},\vec{b}\right]$ notiert.

Die Schreibweise $\vec{a}\wedge\vec{b}$ und die Bezeichnung äußeres Produkt werden nicht nur für das Vektorprodukt verwendet, sondern auch für die Verknüpfung, die zwei Vektoren einen sogenannten Bivektor zuordnet, siehe Graßmann-Algebra.

Komponentenweise Berechnung

In rechtshändigen kartesischen Koordinaten bzw. im reellen Koordinatenraum $\R^3$ mit dem Standardskalarprodukt und der Standardorientierung gilt für das Kreuzprodukt:

$\vec{a}\times\vec{b} = \begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix} \times \begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}\,.$

Ein Zahlenbeispiel:

$\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix} \times \begin{pmatrix}-7 \\ 8 \\ 9 \end{pmatrix} = \begin{pmatrix} 2 \cdot 9 - 3 \cdot 8 \\ 3 \cdot (-7) - 1 \cdot 9 \\ 1 \cdot 8 - 2 \cdot (-7) \end{pmatrix} = \begin{pmatrix} -6 \\ -30 \\ 22 \end{pmatrix}\,.$

Eine Merkregel für diese Formel beruht auf einer symbolischen Darstellung über die Determinante. Dabei notiert man eine $(3 \times 3)$-Matrix, in deren erster Spalte die Symbole $\vec e_1$, $\vec e_2$ und $\vec e_3$ für die Standardbasis stehen. Die zweite Spalte wird von den Komponenten des Vektors $\vec a$ und die dritte von denen des Vektors $\vec b$ gebildet. Diese Determinante berechnet man nach den üblichen Regeln, zum Beispiel indem man sie nach der ersten Spalte entwickelt

$\begin{align} \vec a \times \vec b &=\det \begin{pmatrix}\vec e_1 & a_1 & b_1 \\ \vec e_2 & a_2 & b_2 \\ \vec e_3 & a_3 & b_3\end{pmatrix}\\ &= \vec e_1 \begin{vmatrix} a_2 & b_2 \\ a_3 & b_3 \end{vmatrix} - \vec e_2 \begin{vmatrix} a_1 & b_1 \\ a_3 & b_3 \end{vmatrix} + \vec e_3 \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix} \\ &= (a_2 \,b_3 - a_3 \, b_2) \, \vec e_1 + (a_3 \, b_1 - a_1 \, b_3) \, \vec e_2 + (a_1 \, b_2 - \, a_2 \, b_1) \, \vec e_3 \,, \end{align}$

oder mit Hilfe der Regel von Sarrus:

$\begin{align} \vec a \times \vec b &= \det \begin{pmatrix}\vec e_1 & a_1 & b_1 \\ \vec e_2 & a_2 & b_2 \\ \vec e_3 & a_3 & b_3\end{pmatrix}\\ &= \vec e_1 \cdot a_2 \cdot b_3 + a_1 \cdot b_2 \cdot \vec e_3 + b_1 \cdot \vec e_2 \cdot a_3 \\ &\quad - \vec e_3 \cdot a_2 \cdot b_1 - a_3 \cdot b_2 \cdot \vec e_1 - b_3 \cdot \vec e_2 \cdot a_1 \\ &= (a_2 \,b_3 - a_3 \, b_2) \, \vec e_1 + (a_3 \, b_1 - a_1 \, b_3) \, \vec e_2 + (a_1 \, b_2 - \, a_2 \, b_1) \, \vec e_3 \,. \end{align}$

Mit dem Levi-Civita-Symbol $\varepsilon_{ijk}$ schreibt sich das Kreuzprodukt als

$\vec{a}\times\vec{b} = \sum_{i,j,k=1}^3 \varepsilon_{ijk} a_i b_j \vec e_k\,.$

Eigenschaften

Das Kreuzprodukt ist bilinear, für alle Zahlen $\alpha$, $\beta$ und $\gamma$ und alle Vektoren $\vec a$, $\vec b$ und $\vec c$ gilt

$\vec{a}\times(\beta \,\vec{b} + \gamma\, \vec{c}) = \beta \,(\vec{a}\times\vec{b}) + \gamma \,(\vec{a}\times\vec{c})\,,\ (\alpha\,\vec{a} + \beta\,\vec{b})\times\vec{c} = \alpha\,(\vec{a}\times\vec{c}) + \beta \,(\vec{b}\times\vec{c})\,.$

Das Kreuzprodukt eines Vektors mit sich selbst oder einem kollinearen Vektor ergibt den Nullvektor:

$\vec{a}\times r\vec{a} = \vec{0}\,,$

Das Kreuzprodukt ist antikommutativ. Das heißt, bei Vertauschung der Vektoren wechselt es das Vorzeichen:

$\vec{a}\times\vec{b} = -\, \vec{b}\times\vec{a}\,.$

Für jeden Vektor $\vec v$ gilt:

$\vec v \cdot (\vec a \times \vec b) = \operatorname{det} (\vec v, \vec a, \vec b)$.

Dabei bezeichnet der Malpunkt das Skalarprodukt. Durch diese Bedingung ist das Kreuzprodukt eindeutig bestimmt.

Doppeltes Kreuzprodukt

Graßmann-Identität

Das Kreuzprodukt ist nicht assoziativ. Die Graßmann-Identität (nach Hermann Graßmann), auch Graßmannscher Entwicklungssatz genannt, für das wiederholte Kreuzprodukt von drei Vektoren lautet

$\vec{a}\times\left(\vec{b}\times\vec{c}\right) = \langle \vec{a}, \vec{c} \rangle \vec{b} - \langle \vec{a}, \vec{b} \rangle \vec{c}\,,$

wobei $\langle \cdot , \cdot \rangle$ das Standardskalarprodukt meint. In der Physik wird oft die Schreibweise

$\vec{a}\times\left(\vec{b}\times\vec{c}\right) = \vec{b} \langle \vec{a}, \vec{c} \rangle - \vec{c}\langle \vec{a}, \vec{b} \rangle \,,$

verwendet. Nach dieser Darstellung wird die Formel auch BAC-CAB-Formel genannt.

Jacobi-Identität

Außerdem gilt die Jacobi-Identität, dass die zyklische Summe wiederholter Kreuzprodukte verschwindet:

$\vec{a}\times\left(\vec{b}\times\vec{c}\right) +\vec{b}\times \left(\vec{c}\times\vec{a}\right) +\vec{c}\times \left(\vec{a}\times\vec{b}\right) = 0$

Lagrange-Identität

Für das Skalarprodukt von zwei Kreuzprodukten gilt

$\begin{align} (\vec{a}\times\vec{b}) \cdot (\vec{c}\times\vec{d}) &= (\vec{a}\cdot\vec{c}) (\vec{b}\cdot\vec{d}) - (\vec{b}\cdot\vec{c}) (\vec{a}\cdot\vec{d})\\ &= \begin{vmatrix}(\vec{a}\cdot\vec{c}) & (\vec{a}\cdot\vec{d}) \\ (\vec{b}\cdot\vec{c}) & (\vec{b}\cdot\vec{d}) \end{vmatrix}. \end{align}$

Für das Quadrat der Norm erhält man hieraus

$|\vec{a}\times\vec{b}|^2 = |\vec{a}|^2 \, |\vec{b}|^2 - (\vec{a}\cdot\vec{b})^2 = |\vec{a}|^ 2|\vec{b}|^ 2(1-\cos^ 2 \theta),$

also ist der Betrag des Kreuzproduktes

$|\vec{a}\times\vec{b}| = |\vec{a}| \, |\vec{b}|\, \sin \theta\,.$

Da $\theta$, der Winkel zwischen $\vec a$ und $\vec b$, immer zwischen 0° und 180° liegt, ist $\sin \theta \ge 0.$

Spatprodukt

Die Kombination von Kreuz- und Skalarprodukt in der Form

$(\vec{a} \times \vec{b}) \cdot \vec{c}$

wird als Spatprodukt bezeichnet. Das Ergebnis ist eine Zahl, die dem orientierten Volumen des durch die drei Vektoren aufgespannten Spats (Parallelepipeds) entspricht.

Zusammenhang mit Lie-Algebra

Das Kreuzprodukt lässt sich für beliebige Körper $K$ für den $K$-Vektorraum $K^3$ definieren. Dieser bildet dann mit dem Kreuzprodukt eine Lie-Algebra.

Polare und axiale Vektoren

Bei der Anwendung des Kreuzprodukts auf vektorielle physikalische Größen spielt die Unterscheidung in polare Vektoren (das sind solche, die sich wie Differenzen zweier Ortsvektoren verhalten, zum Beispiel Geschwindigkeit, Beschleunigung, Kraft, elektrische Feldstärke) und axiale Vektoren (die sich wie Drehachsen verhalten, zum Beispiel Winkelgeschwindigkeit, Drehmoment, Drehimpuls, magnetische Flussdichte) eine Rolle. Polaren Vektoren ordnet man die Signatur (oder Parität) +1 zu, axialen Vektoren die Signatur -1.

Bei der vektoriellen Multiplikation mit einem polaren Vektor $\vec b$ wechseln Vektoren ihre Signatur: Ist $\vec a$ ein polarer Vektor, so ist $\vec a\times\vec b$ ein axialer; ist $\vec a$ ein axialer Vektor, so ist $\vec a\times\vec b$ ein polarer. Bei der vektoriellen Multiplikation mit einem axialen Vektor bleibt dagegen die Signatur erhalten.

Kreuzprodukt und Nabla-Operator

In der Vektoranalysis wird das Kreuzprodukt zusammen mit dem Nabla-Operator $\nabla$ verwendet, um den Differentialoperator Rotation zu bezeichnen. Ist $\vec V$ ein Vektorfeld im $\R^3$, so ist

$\operatorname{rot}\vec{V} = \nabla \times \vec{V} = \begin{pmatrix} \frac \partial {\partial x_1} \\[.5em] \frac \partial {\partial x_2}\\[.5em] \frac \partial {\partial x_3} \end{pmatrix} \times \begin{pmatrix}V_1\\[.5em] V_2\\[.5em] V_3 \end{pmatrix} = \begin{pmatrix} \frac{\partial}{\partial x_2} V_3 - \frac{\partial}{\partial x_3} V_2 \\[.5em] \frac{\partial}{\partial x_3} V_1 - \frac{\partial}{\partial x_1} V_3 \\[.5em] \frac{\partial}{\partial x_1} V_2 - \frac{\partial}{\partial x_2} V_1 \end{pmatrix} = \begin{pmatrix} \frac{\partial V_3}{\partial x_2} - \frac{\partial V_2}{\partial x_3} \\[.5em] \frac{\partial V_1}{\partial x_3} - \frac{\partial V_3}{\partial x_1} \\[.5em] \frac{\partial V_2}{\partial x_1} - \frac{\partial V_1}{\partial x_2} \end{pmatrix}$

wieder ein Vektorfeld, die Rotation von $\vec V$.

Formal wird dieses Vektorfeld also als Kreuzprodukt des Nabla-Operators und des Vektorfelds $\vec V$ berechnet. Die hierbei auftretenden Ausdrücke $\tfrac \partial {\partial x_i} V_j$ sind jedoch keine Produkte, sondern Anwendungen des Differentialoperators $\tfrac \partial {\partial x_i}$ auf die Funktion $V_j$. Deshalb sind die oben angeführten Rechenregeln wie z. B. die Graßmann-Identität in diesem Fall nicht gültig. Stattdessen gelten für doppelte Kreuzprodukte mit dem Nabla-Operator besondere Rechenregeln.

Kreuzprodukt im Rⁿ

Das Kreuzprodukt lässt sich für beliebige Dimension $n \ge 2$ auf den $\mathbb{R}^n$ verallgemeinern. Dabei ist das Kreuzprodukt im $\mathbb{R}^n$ kein Produkt von zwei Faktoren, sondern von $n-1$ Faktoren.

Das Kreuzprodukt $\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1}$ der Vektoren $\vec a_1, \dots , \vec a_{n-1} \in \R^n$ ist dadurch charakterisiert, dass für jeden Vektor $\vec v \in \R^n$ gilt

$\vec v \cdot (\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1}) = \operatorname{det} (\vec v, \vec a_1, \dots, \vec a_{n-1}).$

In Koordinaten lässt sich das Kreuzprodukt im $\R^n$ wie folgt berechnen. Es sei $\vec e_i$ der zugehörige $i$-te kanonische Einheitsvektor. Für $n-1$ Vektoren

$\vec a_1 = \begin{pmatrix}a_{11} \\ a_{21} \\ \vdots \\ a_{n1}\end{pmatrix}, \ \vec a_2 = \begin{pmatrix}a_{12} \\ a_{22} \\ \vdots \\ a_{n2}\end{pmatrix}, \ \dots, \ \vec a_{n-1} = \begin{pmatrix}a_{1\, (n-1)} \\ a_{2\, (n-1)} \\ \vdots \\ a_{n\, (n-1)}\end{pmatrix} \in \R^n$

gilt

$\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1} = \det \begin{pmatrix} \vec e_1 & a_{11} & \cdots & a_{1(n-1)} \\ \vec e_2 & a_{21} & \cdots & a_{2(n-1)} \\ \vdots & \vdots & \ddots & \vdots \\ \vec e_n & a_{n1} & \dots & a_{n(n-1)} \end{pmatrix}= \begin{vmatrix} \vec e_1 & a_{11} & \cdots & a_{1(n-1)} \\ \vec e_2 & a_{21} & \cdots & a_{2(n-1)} \\ \vdots & \vdots & \ddots & \vdots \\ \vec e_n & a_{n1} & \dots & a_{n(n-1)} \end{vmatrix},$

analog zu der oben erwähnten Berechnung mit Hilfe einer Determinante.

Der Vektor $\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1}$ ist orthogonal zu $\vec a_1,\vec a_2, ... , \vec a_{n-1}$. Die Orientierung ist so, dass die Vektoren $\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1}, \vec a_1,\vec a_2, ... , \vec a_{n-1}$ in dieser Reihenfolge ein Rechtssystem bilden. Der Betrag von $\vec a_1 \times \vec a_2 \times \cdots \times \vec a_{n-1}$ ist gleich dem $(n-1)$-dimensionalen Volumen des von $\vec a_1,\vec a_2, ... , \vec a_{n-1}$ aufgespannten Parallelotops.

Für $n = 2$ erhält man dabei kein Produkt, sondern nur eine lineare Abbildung

$\R^2 \to \R^2; \ \begin{pmatrix} a_1 \\a_2 \end{pmatrix} \mapsto \begin{pmatrix} a_2 \\ -a_1 \end{pmatrix}$,

die Rotation um 90° im Uhrzeigersinn.

Hieran ist auch zu erkennen, dass die Komponentenvektoren des Kreuzprodukts inklusive des Ergebnisvektors in dieser Reihenfolge – anders als aus dem $\R^3$ gewöhnt – im Allgemeinen kein Rechtssystem bilden; diese entstehen nur in reellen Vektorräumen mit ungeradem $n$, bei geraden $n$ bildet der Ergebnisvektor mit den Komponentenvektoren ein Linkssystem. Dies liegt wiederum daran, dass die Basis $( \vec a_1, \vec a_2, \dotsc, \vec a_{n-1}, \vec a_1 \times \vec a_2 \times \dotsb \times \vec a_{n-1})$ in Räumen geradzahliger Dimension nicht dasselbe ist wie die Basis $(\vec a_1 \times \vec a_2 \times \dotsb \times \vec a_{n-1}, \vec a_1, \vec a_2, \dotsc, \vec a_{n-1})$, die per Definition (siehe oben) ein Rechtssystem ist. Zwar würde eine kleine Veränderung der Definition dazu führen, dass die Vektoren in der erstgenannten Reihenfolge im $\R^n$ stets ein Rechtssystem bilden, nämlich wenn in der symbolischen Determinante die Spalte der Einheitsvektoren ganz nach rechts gesetzt würde. Diese Definition hat sich allerdings nicht durchgesetzt.

Eine noch weitergehende Verallgemeinerung führt auf die Graßmann-Algebren.

Weblinks

 Commons: Kreuzprodukt – Sammlung von Bildern, Videos und Audiodateien

 Wiktionary: Kreuzprodukt – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Java-Applet der Universität von Syracuse zum Vektor- oder Kreuzprodukt
• Kreuzprodukt-Rechner: Berechnet einfach das Kreuzprodukt von zwei Vektoren

Quellen

• Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-97217-3.