De-morgansche Gesetze

Die de-morganschen Gesetze (oft auch de-morgansche Regeln) sind zwei grundlegende Regeln für logische Aussagen. Sie wurden nach dem Mathematiker Augustus De Morgan benannt, obwohl sie bereits dem mittelalterlichen Logiker Wilhelm von Ockham bekannt waren. Sie gelten in allen Booleschen Algebren. Insbesondere sind sie in der Aussagenlogik und der Mengenlehre bedeutsam. In der Technik sind sie bedeutsam für die Erstellung von Verriegelungen und Programmen.
Gesetze[Bearbeiten | Quelltext bearbeiten]
Sie lauten in der Logik:
- nicht (a und b) ist äquivalent zu ((nicht a) oder (nicht b)), sowie
- nicht (a oder b) ist äquivalent zu ((nicht a) und (nicht b)).
In der Mathematik findet man zahlreiche unterschiedliche Darstellungen der de-morganschen Gesetze der Aussagenlogik:
- bzw. mit anderer Notation:
Ihre Entsprechung in der Mengenlehre lautet (dabei sind A das Komplement von A, das Symbol für den Schnitt zweier Mengen und das Symbol für die Vereinigung zweier Mengen):
Die Regeln lassen sich auch für Verknüpfungen beliebig vieler Elemente erweitern. So gilt für jede beliebige endliche, abzählbare oder auch nicht abzählbare Indexmenge I:
- und .
Beweis[Bearbeiten | Quelltext bearbeiten]
Ein formaler Beweis des de-morganschen Gesetzes ¬(a ∧ b) ⇔ ¬a ∨ ¬b im Fitch-Kalkül könnte etwa wie folgt aussehen:
|
Damit ist bewiesen, dass ¬(a ∧ b) → ¬a ∨ ¬b. Für den vollständigen Beweis des Gesetzes muss auch die Implikation in umgekehrter Richtung bewiesen werden:
|
Somit ist auch ¬a ∨ ¬b → ¬(a ∧ b) bewiesen. Da die Implikation nun in beiden Richtungen gezeigt ist, ist damit auch die logische Äquivalenz ¬(a ∧ b) ⇔ ¬a ∨ ¬b bewiesen. Mit ähnlichen Mitteln lässt sich auch das andere de-morgansche Gesetz, ¬(a ∨ b) ⇔ ¬a ∧ ¬b, zeigen.
Wahlweise kann der Beweis aber auch auf anderen Wegen, etwa mit Wahrheitstabellen, geführt werden.
Folgerungen[Bearbeiten | Quelltext bearbeiten]
Eine Konjunktion (UND-Verknüpfung) lässt sich mithilfe des de-morganschen Gesetzes durch drei Negationen und einer Disjunktion (NICHT- beziehungsweise ODER-Verknüpfungen) darstellen:
Entsprechend lässt sich eine Disjunktion durch drei Negationen und eine Konjunktion darstellen:
Anwendung[Bearbeiten | Quelltext bearbeiten]
Die de-morganschen Gesetze haben wichtige Anwendungen in der diskreten Mathematik, der Elektrotechnik, der Physik und der Informatik. Insbesondere werden die de-morganschen Gesetze beim Entwurf von digitalen Schaltungen genutzt, um die Typen der verwendeten logischen Schaltelemente gegeneinander auszutauschen oder Bauteile einzusparen.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Beispiel aus dem Alltag[Bearbeiten | Quelltext bearbeiten]
Angenommen, eine Person trinkt gerne Kaffee: Um nun auszudrücken, dass sie diesen immer nur schwarz und ohne Zucker trinkt, kann sie folgende Aussagen formulieren:
- Wenn Milch oder Zucker enthalten ist, dann trinke ich den Kaffee nicht.
Umgewandelt nach de Morgan und Kontraposition:
- Wenn ich den Kaffee trinke, dann ist keine Milch und kein Zucker enthalten.
Beide Aussagen sind wertgleich.
Beispiel in der Mengenlehre[Bearbeiten | Quelltext bearbeiten]
Es soll anhand der Beziehung
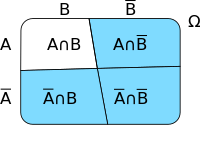
die Gültigkeit der de-morganschen Regeln illustriert werden. Es sind zwei Mengen A und B gegeben, die Teilmengen einer Obermenge Ω sind. Die Grafik 1 zeigt die Lage der Mengen und ihrer Gegenmengen A und B.
In der Grafik 2 wird gezeigt, wie gebildet wird. In der Grafik 3 wird das Komplement zu dargestellt, und man sieht, dass beide Mengen gleich sind.

|
|

|
| Aufteilung der Obermenge in A und B |
Eine Interpretation wäre:
In einer Abnahmeprüfung werden hochwertige Kochmesser daraufhin überprüft, ob die Schneide fehlerfrei ist (Menge A) und ob die Schneide ordnungsgemäß im Griff verankert ist (Menge B). Ein Messer wird nicht angenommen, wenn es zur Menge A oder zur Menge B oder zu beiden gehört, also wenn mindestens eine Beanstandung vorliegt: . Das Messer wird angenommen, wenn es beide Anforderungen erfüllt, wenn es also zur Menge gehört, das heißt, es wird nicht angenommen, wenn es zu gehört.













