Wahrheitstabelle
Eine Wahrheitstabelle oder Wahrheitstafel, auch Wahrheitswert-Tabelle oder Wahrheitsmatrix genannt, ist eine tabellarische Aufstellung des Wahrheitswertverlaufs einer logischen Aussage.
Die Wahrheitstabelle zeigt für alle möglichen Zuordnungen von endlich vielen (häufig zwei) Wahrheitswerten zu den aussagenlogisch nicht weiter zerlegbaren Teilaussagen, aus denen die Gesamtaussage zusammengesetzt ist, welchen Wahrheitswert die Gesamtaussage unter der jeweiligen Zuordnung annimmt. Die Wahrheitstabelle wird genutzt, um Wahrheitswertefunktionen beziehungsweise boolesche Funktionen darzustellen oder zu definieren und um einfache aussagenlogische Nachweise zu führen. Beispielsweise werden Wahrheitstabellen verwendet, um die Bedeutung von Junktoren festzulegen.
Darstellung boolescher Funktionen[Bearbeiten | Quelltext bearbeiten]
Für den zweiwertigen Fall wird der Wahrheitswert „wahr“ im Folgenden als und „falsch“ als bezeichnet.
Für mehrwertige Fälle werden oft numerische Werte im Bereich von bis verwendet (im dreiwertigen Fall z. B. die Werte , und , im fünfwertigen Fall die Werte , , , und ). Im mehrwertigen Fall wird oft nicht von Wahrheitswerten, sondern von Quasiwahrheitswerten oder von Pseudowahrheitswerten gesprochen.
Allgemein gibt es für eine m-wertige Logik, d. h. für eine Logik mit endlich vielen Wahrheitswerten, deren Anzahl m ist, n-stellige wahrheitsfunktionale Junktoren bzw. boolesche Funktionen. Für die zweiwertige Aussagenlogik gibt es also einstellige Junktoren und zweistellige Junktoren. Schon für die dreiwertige Aussagenlogik gibt es einstellige und zweistellige Junktoren.
|
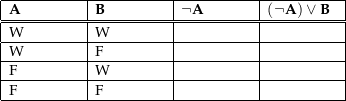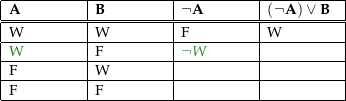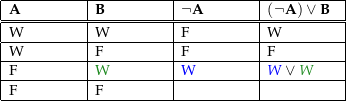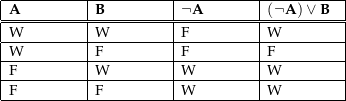
Als ein Beispiel für eine einstellige Wahrheitswertefunktion einer zweiwertigen Logik dient hier die nebenstehende Wahrheitstafel, die das Ergebnis der Anwendung der Negation auf die Aussage in der klassischen Aussagenlogik zeigt. |
Die folgende Tabelle gibt für jeden Wahrheitswert der Aussagen und das Resultat einiger zweiwertiger Verknüpfungen an:
| Belegung | Konjunktion | Disjunktion | materiale Implikation | Äquivalenz Bikonditional | |
|---|---|---|---|---|---|
| AND | OR | Konditional | XNOR | ||
| w | w | w | w | w | w |
| w | f | f | w | f | f |
| f | w | f | w | w | f |
| f | f | f | f | w | w |
Eine besondere Stellung haben folgende nach Henry Maurice Sheffer bzw. Charles Sanders Peirce benannte zweiwertige Funktionen (siehe hierzu Funktionale Vollständigkeit und Shefferscher Strich), denen das NAND- und das NOR-Gatter entsprechen:
| Shefferscher Strich (NAND, ) |
Peirce-Pfeil (NOR, ) | ||
|---|---|---|---|
| w | w | f | f |
| w | f | w | f |
| f | w | w | f |
| f | f | w | w |
In einer dreiwertigen Logik sind 332 = 19 683 zweistellige Verknüpfungen möglich. In der folgenden Tabelle sind zwei von ihnen dargestellt: Die Konjunktion aus der logischen Sprache Ł3 von Jan Łukasiewicz (1920) und die Konjunktion aus dem Kalkül B3 von Dmitrij Anatol'evič Bočvar (1938).
| Belegung | Konjunktion | ||
|---|---|---|---|
| in Ł3 | in B3 | ||
| 1 | 1 | 1 | 1 |
| 1 | ½ | ½ | ½ |
| 1 | 0 | 0 | 0 |
| ½ | 1 | ½ | ½ |
| ½ | ½ | ½ | ½ |
| ½ | 0 | 0 | ½ |
| 0 | 1 | 0 | 0 |
| 0 | ½ | 0 | ½ |
| 0 | 0 | 0 | 0 |
Eine vierwertige Logik hat bis zu mögliche zweistelligen Operatoren. Hier als Beispiel die Wahrheitstafel für das Konditional bzw. die materiale Implikation im logischen System G4 von Kurt Gödel (1932).
| Belegung | Konditional | |
|---|---|---|
| in G4 | ||
| 1 | 1 | 1 |
| 1 | 2⁄3 | 2⁄3 |
| 1 | 1⁄3 | 1⁄3 |
| 1 | 0 | 0 |
| 2⁄3 | 1 | 1 |
| 2⁄3 | 2⁄3 | 1 |
| 2⁄3 | 1⁄3 | 1⁄3 |
| 2⁄3 | 0 | 0 |
| 1⁄3 | 1 | 1 |
| 1⁄3 | 2⁄3 | 1 |
| 1⁄3 | 1⁄3 | 1 |
| 1⁄3 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 2⁄3 | 1 |
| 0 | 1⁄3 | 1 |
| 0 | 0 | 1 |
Beweis- und Entscheidungsverfahren[Bearbeiten | Quelltext bearbeiten]
Wahrheitstabellen eignen sich dazu, einfache aussagenlogische Beweise auf der semantischen Modellebene zu führen, insbesondere für die Gültigkeit von grundlegenden Gesetzen, auf denen logische Beweisverfahren aufbauen. Zum Beispiel zeigt die logische Äquivalenz der 3. und 4. Spalte in den folgenden Wahrheitstabellen die Gültigkeit der De Morganschen Gesetze:
|
|
In der Praxis eignet sich diese Art der Beweisführung allerdings nur für Aussagen mit einer kleinen Anzahl von Aussagenvariablen, da die Größe exponentiell mit der Anzahl der Variablen wächst.
Für die Aussagenlogik mit endlich vielen Wahrheitswerten und klassischem Folgerungsbegriff (siehe Klassische Logik) sind Wahrheitstafeln ein Entscheidungsverfahren für viele wichtige Fragestellungen, das heißt ein Verfahren, mit dem sich die jeweilige Fragestellung für jede Aussage in endlicher Zeit mechanisch entscheiden lässt. So lässt sich mit Hilfe von Wahrheitstafeln die Frage entscheiden, ob eine gegebene Aussage erfüllbar, unerfüllbar oder tautologisch ist (siehe Erfüllbarkeitsproblem der Aussagenlogik); ebenso lässt sich entscheiden, ob ein Argument gültig oder ungültig ist.
Umformung in andere Darstellungsformen[Bearbeiten | Quelltext bearbeiten]
Der Inhalt einer Wahrheitstabelle kann zur weiteren Verarbeitung oder Vereinfachung in andere, äquivalente Darstellungen überführt werden, beispielsweise in ein Karnaugh-Veitch-Diagramm.
Eine Alternative: Wahrheitswertanalyse nach Quine[Bearbeiten | Quelltext bearbeiten]
Wahrheitstabellen sind in vielen Fällen eine rationelle und einfach zu handhabende Methode der Wahrheitswertanalyse. Sie haben jedoch den Nachteil, dass immer alle Fälle durchgegangen werden müssen. Die Anzahl der Fälle steigt aber mit der Anzahl der Variablen (Satzbuchstaben) im Verhältnis an. Bei 2 Variablen gibt es 4 Fälle, bei 3 Variablen 8 Fälle, bei 4 Variablen 16 Fälle usw. Bei vielen Variablen kann die Wahrheitswertanalyse durch Wahrheitstabellen recht aufwändig werden.
Deshalb schlägt Quine in seinem Buch Grundzüge der Logik[1] eine alternative Form der Wahrheitswertanalyse vor. Auf Seite 54 gibt Quine das folgende Beispiel mit drei Variablen bzw. Satzbuchstaben (P, Q und R):
| (P ∧ Q) ∨ (¬P ∧ ¬R) → (Q ↔ R) | |||||||||||||||||||||||||||||||||||||
| (w ∧ Q) ∨ (f ∧ ¬R) → (Q ↔ R) | (f ∧ Q) ∨ (w ∧ ¬R) → (Q ↔ R) | ||||||||||||||||||||||||||||||||||||
| Q ∨ (f ∧ ¬R) → (Q ↔ R) | f ∨ (w ∧ ¬R) → (Q ↔ R) | ||||||||||||||||||||||||||||||||||||
| (Q ∨ f) → (Q ↔ R) | (w ∧ ¬R) → (Q ↔ R) | ||||||||||||||||||||||||||||||||||||
| Q → (Q ↔ R) | ¬R → (Q ↔ R) | ||||||||||||||||||||||||||||||||||||
| w → (w ↔ R) | f → (f ↔ R) | f → (Q ↔ w) | w → (Q ↔ f) | ||||||||||||||||||||||||||||||||||
| w ↔ R | w | w | Q ↔ f | ||||||||||||||||||||||||||||||||||
| R | ¬Q | ||||||||||||||||||||||||||||||||||||
| w | f | f | w | ||||||||||||||||||||||||||||||||||
Der Beispielterm (P ∧ Q) ∨ (¬P ∧ ¬R) → (Q ↔ R) ist also in zwei Fällen falsch: bei P/w|Q/w|R/f und bei P/f|Q/w|R/f. Die Wahrheitstabelle dazu sieht so aus:
| P | Q | R | (P | ∧ | Q) | ∨ | (¬P | ∧ | ¬R) | → | (Q | ↔ | R) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w | w | w | w | w | w | w | f | f | f | w | w | w | w |
| w | w | f | w | w | w | w | f | f | w | f | w | f | f |
| w | f | w | w | f | f | f | f | f | f | w | f | f | w |
| w | f | f | w | f | f | f | f | f | w | w | f | w | f |
| f | w | w | f | f | w | f | w | f | f | w | w | w | w |
| f | w | f | f | f | w | w | w | w | w | f | w | f | f |
| f | f | w | f | f | f | f | w | f | f | w | f | f | w |
| f | f | f | f | f | f | w | w | w | w | w | f | w | f |
Ein einfacheres Beispiel ist die Definition der Implikation:
(A → B) ↔ (¬A ∨ B)
Die Wahrheitstabelle dazu sieht so aus:
| A | B | (A | → | B) | ↔ | (¬A | ∨ | B) |
|---|---|---|---|---|---|---|---|---|
| w | w | w | w | w | w | f | w | w |
| w | f | w | f | f | w | f | f | f |
| f | w | f | w | w | w | w | w | w |
| f | f | f | w | f | w | w | w | f |
Die Wahrheitswertanalyse nach Quine sieht bei diesem Beispiel so aus:
| (A → B) ↔ (¬A ∨ B) | |||||||||||||||||||||
| (w → B) ↔ (f ∨ B) | (f → B) ↔ (w ∨ B) | ||||||||||||||||||||
| (w → w) ↔ (f ∨ w) | (w → f) ↔ (f ∨ f) | (w ↔ w) | |||||||||||||||||||
| (w → w) | (f ↔ f) | w | |||||||||||||||||||
| w | w | ||||||||||||||||||||
Bei der von Quine vorgeschlagenen Methode der Wahrheitswertanalyse werden die Variablen bzw. Satzbuchstaben also schrittweise durch ihre Wahrheitswerte ersetzt. Dabei werden dann zeilenweise Fallunterscheidungen vorgenommen, so dass eine baumartige Struktur entsteht. In beiden Beispielen, dem von Quine und der Definition der Implikation, ist auch zu sehen, dass nicht immer alle Fälle durchgegangen werden müssen, was bei vielen Variablen ein Vorteil gegenüber Wahrheitstabellen sein kann. Durch beide Methoden können die Fälle, in denen ein Term wahr bzw. falsch wird exakt ermittelt werden. Daher leisten beide Methoden dasselbe, sind also äquivalent.
Zur Geschichte[Bearbeiten | Quelltext bearbeiten]
Wenn man unter einer Wahrheitstabelle die homomorphe Zuordnung von Wahrheitswerten zu den in einer Aussage vorkommenden atomaren Aussagen versteht, dann geht die Wahrheitstabelle auf Philon von Megara zurück, der auf diese Weise im 4. Jahrhundert vor unserer Zeitrechnung die Wahrheitsfunktion für die materiale Implikation definierte.[2] Auch in der von Chrysippos von Soloi geprägten stoischen Logik wurden Wahrheitstabellen in diesem Sinn umfassend verwendet.[3]
In der modernen Logik benutzte George Boole 1847 Wahrheitstafeln unter dem Namen „Module einer Funktion“ zur semantischen Entscheidbarkeit von logischen Termen (Funktionen).[4] Später benützten auch Gottlob Frege und Charles Sanders Peirce dieses Entscheidungsverfahren, wobei Peirce den Zweck der Ermittlung von Tautologien deutlicher betonte. Wahrheitstabellen im wörtlichen Sinn als Tabellen wurden allerdings erst 1921 von Emil Leon Post[5] und Ludwig Wittgenstein[6] eingeführt; durch ihren Einfluss wurden Wahrheitstabellen als Verfahren zur Entscheidung für Tautologien Allgemeingut.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Martha Kneale, William Kneale: The Development of Logic. Clarendon Press, 1962, ISBN 0-19-824773-7 (englisch, zur Geschichte).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- PHP-Script zur Ausgabe von Wahrheitstafeln (Open Source)
- Wahrheitstafel-Trainer in JavaScript
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Quine, Willard Van Orman: Grundzüge der Logik. 6. Auflage. Suhrkamp, Frankfurt am Main 1988, ISBN 3-518-27665-4, S. 49–56 (§5 Wahrheitswertanalyse).
- ↑ “The device of tabulation was not introduced until recently, but the idea of truth-functional dependence was obviously quite clear to Philo.” (Martha Kneale, William Kneale: The Development of Logic. Clarendon Press, 1962, ISBN 0-19-824773-7, S. 130 (englisch).); in diesem Sinne auch Bocheński „in Anlehnung an die Antike“ (Bocheński: Formale Logik. 2. Auflage. 1962, S. 384 ff.)
- ↑ “The Stoics gave truth-functional definitions of all the more important propositional connectives […]” (Benson Mates: Stoic Logic (= University of California Publications in Philosophy. Nr. 26). University of California Press, Berkeley 1953, ISBN 0-520-02368-4, S. 42 (englisch, ISBN des Nachdrucks von 1973).)
- ↑ Boole: The Mathematical Analysis of Logic. 1847, S. 60 ff.
- ↑ Emil Leon Post: Introduction to a General Theory of Elementary Propositions. In: American Journal of Mathematics. Band 43, 1921, S. 163–185.
- ↑ Ludwig Wittgenstein: Tractatus Logico-Philosophicus. 1921 (Abschnitt 4.31).
























