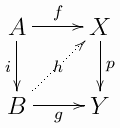Modellkategorie
In der mathematischen Homotopietheorie ist eine Modellkategorie eine Kategorie mit ausgewählten Unterklassen von Pfeilen, die „schwache Äquivalenzen“, „Faserungen“ und „Kofaserungen“ genannt werden. Die Anforderungen an diese Klassen stellen eine Abstraktion der entsprechenden topologischen Begriffe dar und ermöglichen die Konstruktion einer zugehörigen Homotopiekategorie nicht nur für die Kategorie der topologischen Räume, sondern etwa auch für die Kategorie der Kettenkomplexe. In letzterem Fall nennt man die zugehörigen Homotopiekategorien derivierte Kategorien.
Der Begriff wurde im Jahr 1967 von Daniel G. Quillen eingeführt.
Definition[Bearbeiten | Quelltext bearbeiten]
In einer Kategorie seien drei objektgleiche Unterkategorien ausgezeichnet:
- schwache Äquivalenzen
- Faserungen
- Kofaserungen.
Wir nennen (Ko-)Faserungen azyklisch oder trivial, wenn sie zugleich schwache Äquivalenzen sind.
heißt Modellkategorie, wenn die folgenden Axiome erfüllt sind:
MC1 ((Ko-)limites)[Bearbeiten | Quelltext bearbeiten]
ist endlich bivollständig.
MC2 („2 aus 3“)[Bearbeiten | Quelltext bearbeiten]
Sind Pfeile in und zwei von ihnen schwache Äquivalenzen, so auch der dritte.
MC3 (Retrakte)[Bearbeiten | Quelltext bearbeiten]
Ist Retrakt eines Pfeils , der einer der ausgezeichneten Unterkategorien angehört, so gehört derselben Unterkategorie an.
MC4 (Hebung)[Bearbeiten | Quelltext bearbeiten]
Sind in dem kommutativen Diagramm
Cofaserung, Faserung und oder azyklisch, so gibt es einen Pfeil , der mit dem Diagramm kommutiert.
MC5 (Zerlegung)[Bearbeiten | Quelltext bearbeiten]
1. Jeder Pfeil kann als für eine Faserung und eine azyklische Kofaserung dargestellt werden.
2. Jeder Pfeil kann als für eine azyklische Faserung und eine Kofaserung dargestellt werden.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
- Die Definition ist selbstdual: Die duale Kategorie trägt ebenfalls die Struktur einer Modellkategorie, bei der lediglich die Klassen der Faserungen und Kofaserungen vertauscht sind.
- Das Axiom MC4 charakterisiert die Klassen der Faserungen und Kofaserungen: Ein Pfeil ist genau dann Faserung, wenn es zu jedem Diagramm, in dem azyklische Kofaserung ist, eine Hebung gibt (entsprechend für Kofaserungen). Eine Modellkategoriestruktur ist also bereits durch Angabe der schwachen Äquivalenzen und einer der Klassen der Faserungen und Kofaserungen eindeutig festgelegt.
- Die Klasse der Faserungen ist stabil unter Basiswechsel, die der Kofaserungen ist stabil unter Kobasiswechsel.
Fasernde und kofasernde Objekte[Bearbeiten | Quelltext bearbeiten]
Nach MC1 enthält insbesondere ein Anfangsobjekt und ein Endobjekt . Ein Objekt heißt fasernd, wenn Faserung ist, kofasernd, wenn Kofaserung ist.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Topologische Räume[Bearbeiten | Quelltext bearbeiten]
Auf der Kategorie der topologischen Räume wird üblicherweise die folgende Modellkategoriestruktur betrachtet: Als schwache Äquivalenzen werden die schwachen Homotopieäquivalenzen, als Faserungen die Serre-Faserungen gewählt.
Die topologischen Räume lassen sich auch mit einer Modellstruktur versehen, bei der die schwachen Äquivalenzen die Homotopieäquivalenzen sind.
Kettenkomplexe[Bearbeiten | Quelltext bearbeiten]
Die Kategorie der Kettenkomplexe von R-Moduln mit nichtnegativen Indizes hat die folgende Modellkategoriestruktur:
- Als schwache Äquivalenzen werden die Pfeile (also graderhaltende Homomorphismen, die den Ableitungsoperator respektieren) gewählt, die Isomorphismen in der Homologie induzieren.
- Faserungen sind die Pfeile , deren Komponenten für jeden Grad Monomorphismen mit projektivem Kokern sind.
- Kofaserungen sind die Pfeile , für die die in positiven Graden surjektiv sind.
Homotopiekategorie[Bearbeiten | Quelltext bearbeiten]
Um den Begriff der Homotopie auf beliebige Modellkategorien übertragen zu können, werden Zylinderobjekte und Wegobjekte definiert, mit deren Hilfe Links- und Rechtshomotopien definiert werden.
Diese beiden Homotopiebegriffe sind im Allgemeinen weder Äquivalenzrelationen noch stimmen sie miteinander überein. In dem Falle, dass die Quellen und Ziele der betrachteten Pfeile fasernd und kofasernd sind, beschreiben beide Definitionen dieselbe Äquivalenzrelation. Man kann deshalb folgendermaßen zu einer Homotopiekategorie übergehen: Zunächst werden Pfeile funktoriell durch solche ersetzt, die sich nur um schwache Äquivalenzen unterscheiden, aber fasernde und kofasernde Quellen und Ziele haben. Dann kann man Äquivalenzklassen links- bzw. rechtshomotoper Pfeile zu Homotopieklassen zusammenfassen und erhält die Homotopiekategorie.
Da man den Übergang zur Homotopiekategorie auch als Lokalisierung bezüglich der schwachen Äquivalenzen beschreiben kann, braucht man für die Konstruktion der Homotopiekategorie keine Kenntnis der Faserungen und Kofaserungen.
Literatur[Bearbeiten | Quelltext bearbeiten]
- W. G. Dwyer und J. Spalinski: Homotopy Theories and model categories (PDF-Datei; 419 kB), 1995
- Mark Hovey: Model Categories, 1999, ISBN 0-8218-1359-5
- Daniel G. Quillen: Homotopical algebra, Lecture Notes in Mathematics, vol. 43, Springer-Verlag, 1967.
- J. P. May, J. Sigurdsson: Parametrized Homotopy Theory, 2006 [1], ISBN 0-8218-3922-5
- Ken-ichi Maruyama, John W. Rutter: Groups of Homotopy Self-Equivalences and Related Topics, 2001 [2], ISBN 0-8218-2683-2
- Alejandro Adem, Samuel Gitler, R. James Milgram, Douglas C. Ravenel: Homotopy Theory and Its Applications, Contemporary Mathematics, Volume: 188, American Mathematical Society, 1995 [3], ISBN 0-8218-0305-0.
- Simon Salamon, Brian Steer, Wilson Alexander Sutherland: Advances in Homotopy Theory, Cambridge University Press, 1989 [4], ISBN 0-521-37907-5.