Benutzer Diskussion:Bleckneuhaus/Sandkasten

Dieser Artikel ist im Entstehen und noch nicht Bestandteil der freien Enzyklopädie Wikipedia.

Solltest du über eine Suchmaschine darauf gestoßen sein, bedenke, dass der Text noch unvollständig sein und Fehler oder ungeprüfte Aussagen enthalten kann. Wenn du Fragen zum Thema hast, nimm Kontakt mit dem Autor Bleckneuhaus auf.

Boltzmann-Gleichung

Geplanter Abschnitt Herleitung der Bernoulli-Gleichung in der kinetischen Gastheorie

Zum Zusammenhang von Druck und Strömungsgeschwindigkeit

(nach Huang, S. 98)

Mit der (normierten) Verteilungsfunktion $f({\vec {x}},\;{\vec {v}},\;t)\,d^{3}r\,d^{3}v$ der Orte ${\vec {x}}$ und der Geschwindigkeiten ${\vec {v}}$ der Massenpunkte bildet man für einen gegeben Ort und Zeit bestimmte gewichtete Mittelwerte über alle Geschwindigkeiten. Die Mittelung wird durch $\langle ...\rangle$ dargestellt:

$\langle 1\rangle \equiv \int f({\vec {x}},\;{\vec {v}},\;t)\,d^{3}v=n({\vec {x}},\;t)$ ist die makroskopische Teilchendichte. Mit der Teilchenmasse m multipliziert ergibt sich die Dichte $\rho ({\vec {x}},\;t)=m\,n({\vec {x}},\;t)$.

$\langle {\vec {v}}\rangle \equiv \int {\vec {v}}f\,d^{3}v={\vec {u}}({\vec {x}},\;t)$ ist die makroskopische Strömungsgeschwindigkeit.

Die kartesischen Komponenten der Vektoren ${\vec {x}}$, ${\vec {v}}$ bzw. ${\vec {u}}$ werden mit $x_{i}$, $v_{i}$ und $u_{i}$ für $i=\{1,2,3\}$ bezeichnet.

Wenn man die Änderungsrate der Verteilungsfunktion durch die Boltzmannschen Transportgleichung beschreibt und berücksichtigt, dass bei jedem Stoß zweier Teilchen der Gesamtimpuls erhalten bleibt, ergibt die Forderung nach stationären Verhältnissen eine räumliche Bedingung für das Produkt der Dichte mit dem Mittelwert des Produkts von je zwei Geschwindigkeitskomponenten:

$\sum _{j=1}^{3}{\frac {\partial }{\partial x_{j}}}\left(\rho \,\langle \,v_{i}v_{j}\rangle \right)=0$

Aus dieser Gleichung ergibt sich die gegenseitige Abhängigkeit von Strömungsgeschwindigkeit und Druck, die für die Bernoulli-Gleichung charakteristisch ist. Im Einzelnen sieht man das so:

Der Mittelwert des gemischen Produkts $v_{i}v_{j}$ kann durch das Produkt der einzelnen Mittelwerte $u_{i}u_{j}$ und die Varianz ausgedrückt werden:

$\langle v_{i}v_{j}\rangle =u_{i}u_{j}+\langle (v_{i}-u_{i})(v_{j}-u_{j})\rangle$

Das kann durch Ausmultiplizieren leicht gezeigt werden und drückt nur den für jede streuende Größe bekannten Zusammenhang zwischen der Varianz, dem Quadrat des Erwartungswerts und dem Erwartungswert des Quadrats der Größe aus. Nach Multiplikation dieser Gleichung mit der Dichte ist auf der rechten Seite der erste Term durch die massenspezifische kinetische Energie aufgrund der Strömung gegeben, der zweite Term durch den Druck. Denn gemittelt wird hier (komponentenweise) über die Abweichung der Teilchengeschwindigkeit von der Strömungsgeschwindigkeit ${\vec {u}}$:

${\vec {v}}'={\vec {v}}-{\vec {u}}$

${\vec {v}}'$ ist die Teilchengeschwindigkeit, wenn sie in einem mit der Durchschnittsgeschwindigkeit bewegten Bezugssystem betrachtet wird. Die Verteilung dieser Relativgeschwindigkeiten wird als isotrop angesetzt. Die Größe

$P_{ij}=\rho \,\langle v_{i}'v_{j}'\rangle$

bemißt das Ausmaß, in dem die einzelnen Teilchenbewegungen in $i$- und $j$-Richtung korreliert sind. Für $i\neq j$ sind sie unkorreliert, für $i=j$ ist $P_{ii}=\rho \,\langle v_{i}'v_{i}'\rangle ={\frac {1}{3}}\rho \,\langle v'^{2}\rangle =P$, worin $P$ den Druck angibt wie in der kinetischen Gastheorie. $P_{ij}$ wird daher als Drucktensor bezeichnet, er ist das $P$-fache der Einheitsmatrix.

...

Allgemeines

Die Bernoulli-Gleichung für ein strömendes ideales Gas lässt sich im Rahmen der kinetischen Gastheorie verstehen. Dazu geht man von einer Verteilung $f({\vec {r}},\,{\vec {v}},t)$ der Teilchen über die verschiedenen Werte von Raum- und Geschwindigkeitskoordinaten aus, wobei die Teilchen eine Strömung bilden sollen, so dass die Durchschnittsgeschwindigkeit der Teilchen in der Umgebung eines Orts ${\vec {r}}$ nicht null ist, sondern ein evtl. orts- und zeitabhängiger Geschwindigkeitsvektor ${\vec {u}}({\vec {r}},t)$ ist. Für die Abweichungen der individuellen Geschwindigkeiten der Teilchen vom örtlich geltenden Mittelwert ${\vec {u}}({\vec {r}},t)$ wird die Maxwellsche Geschwindigkeitsverteilung zu einer Temperatur $T({\vec {r}},t)$ angenommen, also lokales thermisches Gleichgewicht. Für die zeitliche Veränderung der Verteilungsfunktion aufgrund der paarweisen Zusammenstöße der Teilchen wird die Boltzmannsche Transportgleichung angesetzt. In der Näherung niedrigster (nullter) Ordnung ergibt sich daraus, dass kein Energietransport stattfindet, dass der Druck mit der Temperatur die Zustandsgleichung des idealen Gases erfüllt, dass die Kontinuitätsgleichung und die Eulersche Strömungsgleichung erfüllt sind. Weiter folgt, dass in einem Volumenelement, welches sich mit der Strömungsgeschwindigkeit ${\vec {u}}({\vec {r}},t)$ mitbewegt, nur adiabatische Zustandsänderungen stattfinden. Unter den zusätzlichen Voraussetzungen, dass das Strömungsfeld ${\vec {u}}({\vec {r}})$ wirbelfrei und stationär, also zeitunabhängig ist, und dass die Teilchendichte im ganzen Raum gleich ist, folgt die Bernoullische Druckgleichung.

Geschwindigkeitsverteilung

Animation zur Geschwindigkeitsverteilung in einer Verengung

Mich würde riesig interessieren, wie die Maxwell'sche Geschwindigkeitsverteilung sich bei einer Verengung des Strömungsquerschnitts verhält, und ob sich z.B. dieses einfache Bild darin wiederfindet, nach der die Geschwindigkeitszunahme $\Delta {\vec {u}}$ in Strömungsrichtung einer entsprechenden Abnahme der (mittleren) Geschwindigkeit(skomponente) $\Delta {\vec {v}}$ senkrecht dazu entspricht, weil ja kein Energietransport stattfindet... aber dazu reichen meine mathematischen Fähigkeiten nicht aus, so etwas habe ich zuletzt 1990 gerechnet. liebe Grüße --Dieter F. (Diskussion) 23:36, 3. Feb. 2022 (CET)

ein Gedanke zum hydrodynamischen Paradoxon

hydrodynamisches Paradox

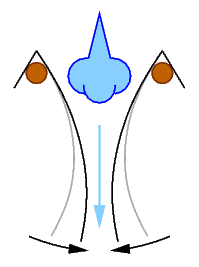
Durch den Satz dass bei steigender Fließgeschwindigkeit der statische Druck abnimmt wird bei der Erklärung des hydrodynamischen Paradox im Artikel zur B.-Gl. m.E. der Eindruck nahegelegt, dass die ausgeblasene Luft (allein) aufgrund ihrer Geschwindigkeit einen geringeren stat. Druck (als die Umgebungsluft) hat, wodurch die Blätter zusammengedrückt werden. Das ist irreführend! Würde das Experiment statt mit gekrümmten Blättern mit ebenen Blättern durchgeführt, passiert nichts dergleichen (zumindest bei einer parallelen Strömung)! Denn die ausgeblasene Luft besitzt - entgegen dem einleitenden Satz - den stat. Druck der Umgebung! Da ist der englische Artikel genauer.

Eine vollständige Erklärung des hydrodyn. Paradox muss in diesem Beispiel m.E. die Krümmung der Blätter mit betonen. Die gekrümmten Blätter stellen eine Verengung des Strömungsquerschnitts dar. Eine solche Verengung ist mit dem hydrodyn. Paradox notwendig verknüpft! Gemäß der Kontinuitätsgleichung steigt in der Verengung die Geschwindigkeit (Venturi-Effekt), wodurch gemäß der Funktionsgleichung (Bernoulli-Effekt) dort ein Unterdruck von $\Delta p={\tfrac {1}{2}}\rho \;\Delta v^{2}$ erzeugt wird.

Könntest du dieser Erklärung zustimmen? -Gruß --Dieter F. (Diskussion) 22:17, 18. Feb. 2022 (CET)