Butler-Volmer-Gleichung
Die Butler-Volmer-Gleichung beschreibt in der Elektrochemie die Reaktionskinetik in der Nähe des Gleichgewichtspotentials Die Stromdichte , welche in der Elektrochemie einer Reaktionsrate entspricht, wird durch die Butler-Volmer-Gleichung in Bezug zur Potentialdifferenz gesetzt. Diese Potentialdifferenz zum Gleichgewichtspotential wird in der Literatur häufig als Durchtrittsüberspannung bezeichnet[1]. Diese Gleichung bildet die Grundlage der elektrochemischen Reaktionskinetik im Gleichgewicht zwischen Oxidations- und Reduktionsreaktionen.
mit folgenden Parametern:
- : Stromdichte [A/m2], definiert als Strom pro Elektrodenoberfläche
- : Austauschstromdichte [A/m2], bezogen auf die Elektrodenoberfläche
- : Elektrodenpotential [V]
- : Gleichgewichtspotential [V]
- : Temperatur [K]
- : Ladungszahl (pro Stoffumsatz der Durchtrittsreaktion übertragene Elektronen)
- : Faraday-Konstante
- : universelle Gaskonstante
- : Ladungstransferkoeffizient für die Oxidationsreaktion (an der Anode) und für die Reduktionsreaktion (an der Kathode).
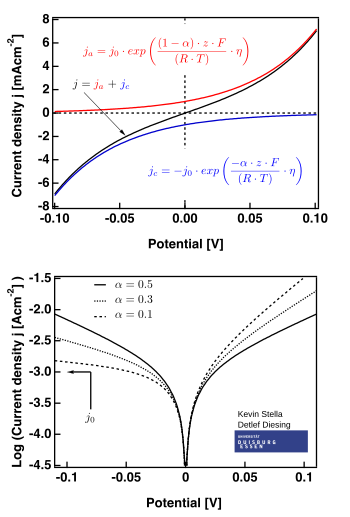
Es wird häufig die vereinfachte Form der Butler-Volmer-Gleichung benutzt, in der man davon ausgeht, dass die Summe aus dem anodischen Ladungstransferkoeffizienten und dem kathodischen Ladungstransferkoeffizienten 1 ergibt.
Damit lässt sich in obige Gleichung einsetzen und es ergibt sich mit :
Die Butler-Volmer-Gleichung lässt sich aus der Kinetik ableiten. Vereinfachend beschreibt sie, dass die Geschwindigkeit einer (elektrochemischen) Reaktion exponentiell von der „treibenden Kraft“ der Reaktion abhängt.
Die heute meist Butler-Volmer-Gleichung genannte Beziehung wurde zuerst 1930 in einer entscheidenden Arbeit von den Chemikern Tibor Erdey-Grúz und Max Volmer veröffentlicht.[2] John Alfred Valentine Butler veröffentlichte 1932 eine entsprechende Arbeit, wobei er 1924 schon Vorarbeit geleistet hatte. Zur Namensgebung dieser Gleichung gab es Diskussionen, die im Journal of Chemical Education der American Chemical Society nachgeschlagen werden können.[3][4]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Volkmar M. Schmidt: Elektrochemische Verfahrenstechnik : Grundlagen, Reaktionstechnik, Prozessoptimierung. Wiley-VCH, Weinheim 2003, OCLC 85820545, S. 94.
- ↑ T. Erdey-Grúz, M. Volmer: Zur Theorie der Wasserstoffüberspannung. In: Zeitschrift für Physikalische Chemie. 150A, 1930, S. 203–213, doi:10.1515/zpch-1930-15020 (PDF).
- ↑ Robert de Levie: What's in a Name? In: Journal of Chemical Education. Band 77, Nr. 5, 1. Mai 2000, doi:10.1021/ed077p610.
- ↑ Robert de Levie: Correction What's in a Name? In: Journal of Chemical Education. Band 88, Nr. 6, 2011, doi:10.1021/ed100894x.




![{\displaystyle j=j_{0}\cdot \left\{\exp \left[{\frac {\alpha _{\mathrm {a} }\cdot z\cdot F}{R\cdot T}}\cdot (E-E_{\mathrm {eq} })\right]-\exp \left[-{\frac {\alpha _{\mathrm {k} }\cdot z\cdot F}{R\cdot T}}\cdot (E-E_{\mathrm {eq} })\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/959336f05d03b2facf84c24e760f78abdc65256b)















![{\displaystyle j=j_{0}\cdot \left\{\exp \left[{\frac {(1-\alpha _{\mathrm {k} })\cdot z\cdot F\cdot \eta }{R\cdot T}}\right]-\exp \left[-{\frac {\alpha _{\mathrm {k} }\cdot z\cdot F\cdot \eta }{R\cdot T}}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc54da7c0e3fdf736c054a47f405fa55915af0a0)