Cardanische Kreise
Als Cardanische Kreise bezeichnet man in der euklidischen Ebene den Sonderfall einer Hypozykloide, bei der der kleine (abrollende) Kreis halb so groß ist wie der große (feste) Kreis. (Der kleine Kreis rollt im Innern des großen Kreises.) Das Besondere dieser speziellen Hypozykloide ist: Jeder Punkt des Kreisbogens des kleinen Kreises bewegt sich auf einem Durchmesser des großen Kreises.
Geschichte[Bearbeiten | Quelltext bearbeiten]

Die Himmelsscheibe von Nebra enthält einen Mechanismus ähnlich der cardanischen Kreise (in der Himmelsscheibe von Nebra finden sich Ellipsen anstelle von Kreisen).[1]
In der englischen Literatur nennt man diese spezielle Hypozykloide Tusi couple (Tusi-Paar[2]) nach dem persischen Astronomen und Mathematiker Nasir ad-Din at-Tusi des 13. Jahrhunderts. Nasir ad-Din at-Tusi beschrieb die Cardanische Kreise in seinem Werk Tahrir al-Majisti aus dem Jahr 1247.[3] Der Begriff „Tusi couple“ wurde aber erst 1966 von Edward Kennedy geprägt.
Der Zusammenhang, dass jeder Punkt des Kreisbogens des kleineren Kreises sich auf einem Durchmesser des größeren Kreises bewegt, wurde 1570 von dem italienischen Humanisten Gerolamo Cardano beschrieben,[4] auf den sich die deutschsprachige Benennung „Cardanische Kreise“ bezieht. Diese frühen Untersuchungen zu Zykloiden wurden später von Galilei ausgeweitet.

Die Verbindung zwischen der Arbeit von Nasir ad-Din at-Tusi und den europäischen Gelehrten wird angenommen, jedoch konnte die Verbindung noch nicht sicher rekonstruiert werden. Auffallend ist, dass in den Arbeiten von Kopernikus[5] die Punkte phonetisch ähnlich benannt wurden wie in den Arbeiten von Tusi.[6][7] Nach Arthur Koestler nutzte Kopernikus in seinem Hauptwerk diese Konstruktion zur Auflösung (scheinbarer) linearer Pendelbewegungen von Erde und anderen Planeten in je zwei Kreisbewegungen.[8]
Formulierung und Beweis des Satzes von Cardano[Bearbeiten | Quelltext bearbeiten]

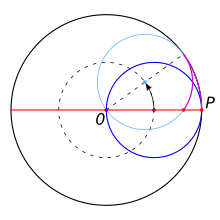
Gegeben ist ein Kreis k (blau) mit Mittelpunkt M und Radius r, der in einem Kreis K (schwarz) mit Mittelpunkt O und dem doppelten Radius R=2r liegt und diesen im Punkt P berührt (s. Bild).
Dann gilt:
- Beim Abrollen des kleinen Kreises im Innern des großen Kreises bewegt sich der am kleinen Kreis fixierte Punkt auf einem Durchmesser des großen Kreises.
Zusatz: Jeder Punkt der Kreislinie des kleinen Kreises bewegt sich auf einem Durchmesser des großen Kreises.
Beweis:
Zum Beweis stellt man sich die Bewegung des Punktes in zwei Drehbewegungen zerlegt vor: 1) Drehung um den Punkt um den Winkel und 2) Drehung um den neuen Mittelpunkt des kleinen Kreises um den Winkel . Benutzt man komplexe Zahlen und ihre Darstellung als Gaußsche Zahlenebene, so ist
- und
- .
Das Bild des Punktes (reelle Zahl !) ist dann:
- .
Die Bahn des Punktes ist also das reelle Intervall (Durchmesser des großen Kreises.)

Technische Anwendungen[Bearbeiten | Quelltext bearbeiten]

Wird der äußere Kreis innen verzahnt und der innere Kreis als Zahnrad ausgeführt, dann lässt sich mit Hilfe Cardanischer Kreise eine Rotationsbewegung in eine periodische geradlinige Bewegung umsetzen.
Buchdruckpressen[Bearbeiten | Quelltext bearbeiten]
Dieses Prinzip lag der Erfindung der Buchdruckschnellpressen von König & Bauer zugrunde.
Motoren[Bearbeiten | Quelltext bearbeiten]
James White erhielt 1801 von Napoleon Bonaparte eine Medaille für eine Dampfmaschine, die eine hypocykloidische Geradführung verwendete. Nach Whites Entwurf wurden ein paar Maschinen gebaut, der wirtschaftliche Erfolg blieb aber aus.[9][10][11]
Matthew Murray entwickelte eine hypocykloidische Dampfmaschine im Jahr 1802.[12][13]
Allgemein[Bearbeiten | Quelltext bearbeiten]
In der technischen Anwendung ist der Mechanismus auch als hypocykloidische Geradführung bekannt.[14][15]
In der Getriebesammlung von Franz Reuleaux finden sich zwei Modelle hypocykloidischer Geradführungen.[16][17]
Hypotrochoiden[Bearbeiten | Quelltext bearbeiten]
Eine Eigenschaft der cardanischen Kreise ist, dass Punkte auf dem inneren Kreis, die nicht auf der Kreislinie liegen, Ellipsen beschreiben. Diese Ellipsen, und die gerade Linie, die vom klassischen cardanischen Kreis beschrieben werden, sind besondere Fälle von Hypotrochoiden.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Girolamo Cardano: Opus novum de proportionibus, Basel 1570. (Archimedes Project)
- Otto Lueger: Lexikon der gesamten Technik und ihrer Hilfswissenschaften. Bd. 2 Stuttgart/ Leipzig 1905, S. 423–424
Weblinks[Bearbeiten | Quelltext bearbeiten]
- https://www.tu-chemnitz.de/mb/MechAntrTech/getriebebibliothek/DB_index.php?TAB=Getriebemodell&NR=147 (Modell zur Verwendung der Cardanischen Kreise in der Getriebetechnik)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ http://sternwarte-recklinghausen.de/astronomie/himmelscheibe-von-nebra/
- ↑ http://sternwarte-recklinghausen.de/astronomie/himmelscheibe-von-nebra/
- ↑ http://www.columbia.edu/~gas1/project/visions/case1/sci.2.html
- ↑ Gerolamo Cardano (1501–1576), Opus novum de proportionibus, 1570
- ↑ Nikolaus Kopernikus: Wie die wechselseitige Bewegung der Libration aus Kreisbewegungen besteht. In: De revolutionibus orbium coelestium, Buch 3, Kapitel 4 (alternativer Link).
- ↑ http://www.columbia.edu/~gas1/project/visions/case1/sci.2.html
- ↑ http://adsabs.harvard.edu/full/1973JHA.....4..128V
- ↑ Arthur Koestler, Die Nachtwandler, Alfred Scherz Verlag Bern 1963, S. 193
- ↑ http://www.mirrorservice.org/sites/gutenberg.org/2/7/1/0/27106/27106-h/27106-h.htm
- ↑ http://www.gutenberg.org/files/27106/27106-h/27106-h.htm
- ↑ Robert Stuart: Historical and Descriptive Anecdotes of Steam-engines, and of Their Inventors and Improvers. Wightman and Cramp, 1829, S. 634 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Archivierte Kopie ( des vom 27. März 2019 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ http://dampfundmehr.de/im-bau/Hypocycloidal/hypo_7.htm
- ↑ http://de.academic.ru/dic.nsf/technik/9302/Geradf%C3%BChrung%2C_hypocykloidische
- ↑ http://www.zeno.org/Lueger-1904/A/Geradf%C3%BChrung,+hypocykloidische
- ↑ http://kmoddl.library.cornell.edu/model.php?m=137
- ↑ http://kmoddl.library.cornell.edu/model.php?m=278











![{\displaystyle [-2r,2r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9c7de55acfd7ae334fedbdb38fb4a5bef8bd4d6)