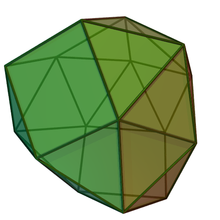
Disphenocingulum Drahtgittermodell eines DisphenocingulumsKörpernetz eines DisphenocingulumsDas Disphenocingulum ist ein Ikositetraeder mit 20 kongruenten gleichseitigen Dreiecken und 4 kongruenten Quadraten als Flächen, 16 Ecken und 38 Kanten. An vier der Ecken grenzen vier Kanten und an die anderen zwölf Ecken grenzen fünf Kanten an. Im Körper gibt es zwei Kanten, die jeweils 2 Quadrate miteinander verbinden. Diese zwei Kanten sind orthogonal und windschief .
Es ist der Johnson-Körper J90 aus einer Reihe von 92 nach dem Mathematiker Norman Johnson benannten Körpern.
Die kartesischen Koordinaten der Eckpunkte können lauten, bei Mittelpunkt im Ursprung und Kantenlänge 2:
(
0
,
±
1
,
p
)
(
±
s
,
±
1
,
q
)
(
0
,
±
t
,
r
)
(
±
t
,
0
,
−
r
)
(
±
1
,
±
s
,
−
q
)
(
±
1
,
0
,
−
p
)
{\displaystyle {\begin{alignedat}{4}&(&0,&&\;\pm 1,&&\;p&)\\&(&\pm s,&&\;\pm 1,&&\;q&)\\&(&0,&&\;\pm t,&&\;r&)\\&(&\pm t,&&\;0,&&\;-r&)\\&(&\pm 1,&&\;\pm s,&&\;-q&)\\&(&\pm 1,&&\;0,&&\;-p&)\end{alignedat}}}
Nach dem Satz von Pythagoras gilt:
(
p
−
q
)
2
+
s
2
=
4
{\displaystyle (p-q)^{2}+s^{2}=4}
(
p
−
r
)
2
+
(
t
−
1
)
2
=
4
{\displaystyle (p-r)^{2}+(t-1)^{2}=4}
4
q
2
+
s
2
+
(
t
−
s
)
2
=
4
{\displaystyle 4q^{2}+s^{2}+(t-s)^{2}=4}
2
q
2
+
(
s
−
1
)
2
=
2
{\displaystyle 2q^{2}+(s-1)^{2}=2}
(
q
+
r
)
2
+
(
t
−
s
)
2
=
3
{\displaystyle (q+r)^{2}+(t-s)^{2}=3}
mit
p
=
a
+
b
2
≈
2
,
21
q
=
a
+
b
2
−
2
a
≈
0
,
93
r
=
b
−
a
2
≈
0
,
65
s
=
2
a
a
2
−
1
≈
1
,
53
t
=
4
−
a
2
+
1
≈
2
,
25
{\displaystyle {\begin{aligned}p&={\frac {a+b}{2}}\approx 2{,}21\\q&={\frac {a+b}{2}}-{\frac {2}{a}}\approx 0{,}93\\r&={\frac {b-a}{2}}\approx 0{,}65\\s&={\frac {2}{a}}{\sqrt {a^{2}-1}}\approx 1{,}53\\t&={\sqrt {4-a^{2}}}+1\approx 2{,}25\end{aligned}}}
bestehend aus
b
=
2
a
+
3
−
(
4
−
a
2
+
1
−
2
a
a
2
−
1
)
2
≈
2
,
86
{\displaystyle b={\frac {2}{a}}+{\sqrt {3-\left({\sqrt {4-a^{2}}}+1-{\tfrac {2}{a}}{\sqrt {a^{2}-1}}\right)^{2}}}\approx 2{,}86}
a
≈
1,558
86993226
{\displaystyle a\approx 1{,}55886993226}
4
=
2
(
2
a
a
2
−
1
−
1
)
2
+
(
3
−
(
4
−
a
2
−
2
a
a
2
−
1
+
1
)
2
+
a
−
2
a
)
2
{\displaystyle 4=2\left({\frac {2}{a}}{\sqrt {a^{2}-1}}-1\right)^{2}+\left({\sqrt {3-\left({\sqrt {4-a^{2}}}-{\tfrac {2}{a}}{\sqrt {a^{2}-1}}+1\right)^{2}}}+a-{\frac {2}{a}}\right)^{2}}
Größen eines Disphenocingulums mit Kantenlänge a
Oberflächeninhalt
A
O
=
a
2
(
4
+
5
3
)
{\displaystyle A_{O}=a^{2}\left(4+5{\sqrt {3}}\right)}