Hydraulischer Durchmesser
Der hydraulische Durchmesser ist eine rechnerische Größe, die zur Berechnung von Druckverlust und Durchsatz in Rohren oder Kanälen herangezogen werden kann, wenn der Querschnitt des Rohres bzw. Kanals von der Kreisform abweicht. Die Anwendung des hydraulischen Durchmessers stellt für turbulente Strömungen eine gute Näherung dar, für laminare Strömungsverhältnisse kann sie jedoch zu erheblichen Fehlern führen.
Der hydraulische Radius ist ähnlich wie der hydraulische Durchmesser definiert und wird vor allem zur Berechnung von Strömungen in offenen Gerinnen angewendet.
Hydraulischer Durchmesser[Bearbeiten | Quelltext bearbeiten]
Definition[Bearbeiten | Quelltext bearbeiten]
Für Rohre mit kreisförmigem Querschnitt sind die Strömungsverhältnisse umfangreich dokumentiert. Die Berechnung des hydraulischen Durchmessers kann man als Versuch verstehen, für einen Strömungskanal mit einem beliebigen Querschnitt den Durchmesser desjenigen Rohres mit kreisförmigem Querschnitt zu ermitteln, das bei gleicher Länge und gleicher mittlerer Strömungsgeschwindigkeit den gleichen Druckverlust wie der gegebene Strömungskanal aufweist.
Bei einer ausgebildeten Rohrströmung stehen die Scherkräfte an der Rohrwand eines bestimmten Rohrabschnitts im Gleichgewicht mit den Druckkräften, die auf die Querschnittsflächen an der Zu- und Abströmung dieses Rohrabschnitts auftreten. Die Definition des hydraulischen Durchmessers geht von der Vorstellung aus, dass vergleichbare Verhältnisse vorliegen, wenn die Querschnittsfläche und der benetzte Umfang im gleichen Verhältnis zueinander stehen. Dabei ist bei Betrachtung des Querschnitts der benetzte Umfang die Länge der Kurve, an der das Fluid die Rohrwand berührt.
Beispiele[Bearbeiten | Quelltext bearbeiten]
- Für die Strömung in einem Ringspalt der Breite zwischen zwei konzentrischen Rohren mit den Durchmessern D bzw. d ergibt sich
- Für einen Kanal mit quadratischem Querschnitt der Seitenlänge ergibt sich der hydraulische Durchmesser zu
Begrenzte Anwendbarkeit[Bearbeiten | Quelltext bearbeiten]
Für die meisten in der Praxis vorhandenen Fälle lassen sich mit Hilfe des hydraulischen Durchmessers die tatsächlich herrschenden Strömungsverhältnisse mit brauchbarer Genauigkeit ermitteln. Es können sich allerdings relevante Abweichungen ergeben, wenn die Form des Querschnitts auf bestimmte Weise von einem Kreis abweicht oder wenn laminare Strömungsverhältnisse vorliegen. Dazu hier zwei Beispiele:
- Form des betrachteten Querschnitts:
- Für einen Querschnitt, der sich aus einem Kreis (Durchmesser d) und einem langen engen Spalt (Spaltbreite b) zusammensetzt („Kreis mit schmalem Fortsatz“) ergibt sich:
- Damit wäre , woraus man einen höheren Druckverlust als im runden Rohr ermitteln würde. Tatsächlich hat der Spalt, sofern er eng genug ist, keinerlei Auswirkung auf den Druckverlust.
- Laminare Spaltströmung:
- Für einen niedrigen breiten Spalt (Spaltbreite Spalthöhe ) ergibt sich ein hydraulischer Durchmesser von:
- Der Druckverlust in einem runden Rohr bei laminarer Strömung und mittlerer Geschwindigkeit ist mit dem Gesetz von Hagen-Poiseuille
- Damit wäre der Druckverlust im Spalt
- .
- Für den niedrigen breiten Spalt lässt sich nach Hagen-Poiseuille auch direkt eine exakte Lösung angeben. Diese lautet
- .
- Die Berechnung unter Zuhilfenahme von liefert in diesem Fall also einen um 33 % zu geringen Druckverlust.
Hydraulischer Radius[Bearbeiten | Quelltext bearbeiten]
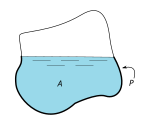
mit A = durchströmte Fläche, P = benetzter Umfang
Der hydraulische Radius ist der Quotient aus dem Strömungsquerschnitt A und dem benetzten Umfang :
Besonders im Fall offener Gerinne ist bequemer anwendbar als .
Beispiele für den hydraulischen Radius[Bearbeiten | Quelltext bearbeiten]
 |
 |
 |
 |
 | |
|---|---|---|---|---|---|
| Breite | oder |
||||
| Mittlere Wassertiefe | |||||
| Querschnittsfläche | |||||
| benetzter Umfang |
[1] | ||||
| Hydraulischer Radius | [1] |





























![{\displaystyle \left[{\frac {\theta -\sin \theta }{\sin {\frac {\theta }{2}}}}\right]{\frac {D}{8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd337dfe3043ea4b8d9bff4833023727c088ba28)














![{\displaystyle {\frac {1}{4}}\left[1-{\frac {\sin \theta }{\theta }}\right]D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8edbced6d2b2aabafd894e05f762f8a314209ea1)



![{\displaystyle \textstyle \xi >1:P=\left({\frac {B}{2}}\right)\left[{\sqrt {1+\xi ^{2}}}+{\frac {1}{\xi }}\ln \left(\xi +{\sqrt {1+\xi ^{2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c8245043f74a85e776ded1ab5719e10eb3071df)