Physikalische Akustik

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Physikalische Akustik behandelt die physikalischen Grundlagen der Akustik, die auf Schwingungen beruhen.

Das menschliche Ohr

Unstretched

Spektrum des Klanges einer akustischen Gitarre

CPT-Sound-Sampling-Rate

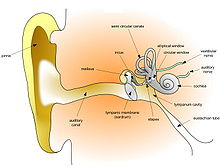
Die physikalische Akustik handelt von den longitudinalen Wellen, den Schallwellen, die vom Ohr wahrgenommen werden. Das Ohr als Schallempfänger reagiert auf Schallwellen mit Frequenzen zwischen 20 Hz und 20 000 Hz, Schallwellen höherer Frequenz rechnet man dem Ultraschall zu. Schallwellen stellen eine sich ausbreitende Folge von Luftverdichtungen und -verdünnungen dar. Die einzelnen Luftteilchen schwingen dabei nur jeweils innerhalb kleiner Bereiche. Eine Schallwelle transportiert keine Materie. Bei Schallschwingungen unterscheidet man zwischen Ton, Klang, Geräusch und Knall, wobei sich ein reiner Ton mit einer Sinuskurve darstellen lässt. Beim Knall hat die Schwingung eine große, schnell abklingende Amplitude.

Schallgeber

Schallgeber sind Platten und Membranen. Sie werden zur Schallerzeugung bspw. im Telefon und Lautsprecher verwendet. Auch schwingende Saiten sind lineare Schallgeber. Sie können längs einer Linie die Luft zu Schwingungen anregen, aber die von der Vorder- und Rückseite der Saite ausgehenden Schwingungen löschen sich durch Interferenz nahezu aus. Bei Musikinstrumenten spannt man daher Saiten auf einen Holzkasten, um die Resonanz zu verstärken, bei bestimmten Abmessungen wirkt dabei der Holzkasten als Resonanzkörper. Bei Saiteninstrumenten ist es wichtig, dass die Eigenfrequenz durch den Resonanzboden des Instruments verstärkt wird.

Für schwingende Saiten gilt folgende Gleichung:

$\nu ={\frac {1}{2l}}\,{\sqrt {\frac {F}{\rho A}}}$

Dabei ist $l$ die Länge der Saite, $\nu$ die Frequenz der schwingenden Saite, $F$ die Kraft, mit der die Saite gespannt wird, $\rho$ die Dichte des Saitenmaterials und $A$ der Querschnitt der Saite.

Tonleiter

In der Musik gibt es die Tonleiter, die aus den acht Tönen c d e f g a h c besteht, wobei jeweils zwei Töne in bestimmtem Frequenzverhältnis stehen: Prime, Sekunde, Terz, Quarte, Quinte, Sexte, Septime, Oktave (Intervall). Die 12 Halbtonintervalle besitzen kein einheitliches Frequenzverhältnis. Bei der physikalischen Stimmung geht man vom eingestrichenen C aus und setzt ν (c') = 256 Hz, für die internationale Stimmung gilt der Kammerton a' mit ν (a') = 440 Hz.

Schallempfänger

Schallempfänger sind Instrumente, die auf Druckschwankungen einer Schallwelle reagieren, wie bspw. das Ohr. Auch Mikrofone sind Schallempfänger. Druckschwankungen erregen eine Membran zu Schwingungen. Diese werden in elektrische Stromschwankungen umgewandelt, die mit einem geeigneten Instrument nachgewiesen werden können.

Der Mensch empfindet Töne als Konsonanz (wohlklingend), wenn sich die Frequenzverhältnisse durch ganze Zahlen nicht größer als acht ausdrücken lassen, sonst als Dissonanz.

Das Ohr

Die Empfindung, die das Ohr von einer reinen Sinusschwingung der Luft wahrnimmt, bezeichnet man als physikalisch einfachen oder reinen Ton. Die Tonhöhe hängt von der Frequenz ab. Je größer die Frequenz, umso höher der Ton. Die Lautstärke hängt von der Amplitude der Sinusschwingung ab. Je größer die Amplitude, umso lauter der Ton. Die Empfindung, die das Ohr von einer periodischen, aber nicht sinusförmigen Schwingung hat, bezeichnet man als Klang. Dabei entstehen Frequenzen der harmonischen Oberschwingungen bzw. Obertöne in ganzzahligem Verhältnis zur Grundschwingung (Grundton). Für die Klagempfindung des Ohrs gilt das Ohmsche Gesetz der Akustik: Der Klang hängt nur von den Frequenzen und Amplituden ab, jedoch nicht von den Phasenunterschieden.

Resonanz als Grundlage der Akustik

Resonanzerscheinungen können bei allen gekoppelten Schwingungssystemen auftreten. Wenn die Frequenz ω gleich der Eigenfrequenz des Oszillators ist, besitzt die Schwingung an der Stelle ein Maximum. Es tritt Resonanz auf. Die Eigenfrequenz eines Systems wird daher Resonanzfrequenz genannt. Bei schwacher Dämpfung ist die Resonanzkurve schmal, man spricht von einer scharfen Resonanz, für starke Dämpfung ist die Resonanzkurve entsprechend breit. Wird ein Glas angeschlagen, dann erzeugt es einen Ton in der Eigenfrequenz des Glases, der in Abhängigkeit von der Dämpfung mehr oder weniger lang zu hören ist. Ein Glas mit geringer Dämpfung kann durch eine intensive Schallwelle bei einer Frequenz, die sehr nahe an der Eigenfrequenz des Glases ist, durch die auftretenden Resonanzschwingungen zerspringen.

Auch in der Akustik gilt für reine Töne -ohne Berücksichtigung der Dämpfung- dieselbe Schwingungsgleichung wie für den harmonischen Oszillator:

$x(t)=u\,\sin(\omega _{0}t+\varphi )$,

wobei ω die Resonanzfrequenz, φ die Phasenverschiebung und u die Amplitude ist.

Interferenz

→ Hauptartikel: Interferenz (Physik)

• Für die Überlagerung von Schallwellen gelten dieselben Gesetzmäßigkeiten wie für andere Wellenarten.

Schwebung zweier Sinusfunktionen

• Die Überlagerung zweier Schallwellen gleicher Ausbreitungsrichtung ergibt bei geringer Frequenzdifferenz eine Schwebung.
• Die Amplitude der resultierenden Welle nimmt periodisch ab und zu.

Schallstärke

• Die Mindeststärke, die ein Schall haben muss, um wahrgenommen zu werden, ist die Hörschwelle, die obere Grenze ist die Schmerzgrenze.
• Als Schallpegel bezeichnet man den 10-fachen dekadischen Logarithmus zweier Schallstärken. Die Einheit ist Dezibel.
• Die Lautstärke, mit der ein Mensch eine Schallstärke subjektiv empfindet, hängt vom Gehörsinn ab und ist eine physiologische Größe mit der Einheit phon.

Ultraschall

Frequenzen oberhalb des Hörbereiches bezeichnet man als Ultraschall.

Literatur

• H. Kuchling: Taschenbuch der Physik, Harry Deutsch Verlag (1986), 314–339, ISBN 3-87144-097-3.

Weblinks

• Literatur von und über Physikalische Akustik im Katalog der Deutschen Nationalbibliothek