Random-Phase-Approximation
Die Random-Phase-Approximation (englisch random-phase approximation, RPA, dt. etwa ‚Näherung zufälliger Phase‘) ist ein Näherungsverfahren zur Behandlung quantenmechanischer Vielteilchensysteme, das die Hartree-Fock-Näherung oder allgemeiner die Molekularfeldtheorie generalisiert und manchmal auch als dynamische Hartree-Fock-Näherung bezeichnet wird. Das Verfahren wird beispielsweise in der Kernphysik zur Beschreibung von kollektiven Anregungen benutzt.
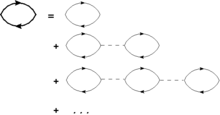
Durchgezogene Linien stehen hier für wechselwirkende bzw. nicht-wechselwirkende greensche Funktionen, gestrichelte Linien für Zwei-Teilchen-Wechselwirkungen.
Die RPA ist ein mikroskopisches Verfahren, um die Struktur von kollektiven Anregung ausgehend von 1-Teilchen-1-Loch-Zuständen zu beschreiben, was einer einfachen diagrammatischen Näherung entspricht (Aufsummation sogenannter Bubble-Diagramme).
Die Methode ist verwandt mit der Tamm-Dancoff-Näherung (TDA), unterscheidet sich aber dadurch, dass auch Grundzustandskorrelationen möglich sind.
Spezialfälle sind die quasiparticle random-phase approximation (QRPA), relativistic random-phase approximation (RRPA), continuum quasiparticle random-phase approximation (CQRPA), relativistic quasiparticle random-phase approximation (RQRPA).
Die Methode wurde von David Bohm und David Pines in den 1950er Jahren für Elektronengase eingeführt[1][2][3] und 1957 von Keith Brueckner und Murray Gell-Mann als Summierung von Feynmandiagrammen interpretiert[4], was eine wesentliche Stütze der damals umstrittenen RPA-Theorie war.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ David Bohm, David Pines: A Collective Description of Electron Interactions. I. Magnetic Interactions. In: Physical Review. Band 82, Nr. 5, 1. Juni 1951, S. 625–634, doi:10.1103/PhysRev.82.625.
- ↑ David Pines, David Bohm: A Collective Description of Electron Interactions: II. Collective vs Individual Particle Aspects of the Interactions. In: Physical Review. Band 85, Nr. 2, 15. Januar 1952, S. 338–353, doi:10.1103/PhysRev.85.338.
- ↑ David Bohm, David Pines: A Collective Description of Electron Interactions: III. Coulomb Interactions in a Degenerate Electron Gas. In: Physical Review. Band 92, Nr. 3, 1. November 1953, S. 609–625, doi:10.1103/PhysRev.92.609.
- ↑ Murray Gell-Mann, Keith A. Brueckner: Correlation Energy of an Electron Gas at High Density. In: Physical Review. Band 106, Nr. 2, 15. April 1957, S. 364–368, doi:10.1103/PhysRev.106.364.