Graham Scan

Der Graham Scan (nach Ronald Graham 1972) ist ein effizienter Algorithmus zur Berechnung der konvexen Hülle einer endlichen Menge von Punkten in der Ebene. Bei $n$ Punkten liegt seine asymptotische Laufzeit in $\mathcal O(n \cdot \log n)$.

Beschreibung

Vorbereitung

Sortierung einer Punktmenge nach Winkel mit Bezugspunkt $P_0$.

Sei $S = \{P\}$ eine endliche Punktmenge. Der Algorithmus beginnt mit einem Punkt der Menge, welcher garantiert ein Eckpunkt der konvexen Hülle ist. Man sucht sich dazu den Punkt mit der kleinsten Ordinate. Sind dies mehrere, so sucht man sich aus diesen Punkten den mit der kleinsten Abszisse aus (lexikographische Suche). Diese Suche kann in $O(n)$ Schritten durchgeführt werden. Nachdem der Startpunkt $P_0$ gefunden wurde, sortiert der Algorithmus die restlichen Punkte $P$ in $S$ nach aufsteigendem Winkel zwischen $P_0$ → $P$ und der x-Achse gegen den Uhrzeigersinn. Haben dabei zwei Punkte den gleichen Winkel (d. h. liegen mit $P_0$ auf einer Linie, sind kollinear mit $P_0$), so wird der Punkt, welcher näher an $P_0$ liegt, verworfen.

Hilfsfunktion

PAB und ABC sind positiv orientierte Dreiecke, BCD ist negativ orientiert. Oder anders, C liegt links von AB, D liegt rechts von BC. Der Stack wird bis [P,A,B,C] aufgebaut, im nächsten Schritt wird C zugunsten von D entfernt.

In der nachfolgenden Rechnung muss wiederholt entschieden werden, ob drei Punkte A=(x_A,y_A), B=(x_B,y_B), C=(x_C,y_C) in der Ebene ein positiv orientiertes Dreieck bilden. Äquivalente Formulierungen dafür sind, dass der Streckenzug A-B-C einen Knick nach links hat oder dass der Punkt C links der Strecke von A nach B bzw. der Punkt B rechts von der Strecke von A nach C liegt.

Diese Aufgabe kann man durch Bestimmen aller relevanten Winkel lösen, oder einfacher durch die Berechnung einer Determinante $T(A, B, C)$, diese liefert das gewünschte Ergebnis mit weniger Rechenaufwand (fünf Subtraktionen, zwei Multiplikationen) und genauer. Das Ergebnis bleibt für rationale Koordinaten im rationalen Zahlenbereich, welcher ohne Verlust von Genauigkeit im Computer abgebildet werden kann. Das Ergebnis wird über den folgenden Ausdruck berechnet.

$\begin{align} T(A, B, C) &= \begin{vmatrix} 1&x_A&y_A\\ 1&x_B&y_B\\ 1&x_C&y_C \end{vmatrix} = \begin{vmatrix} 1&x_A & y_A\\ 0&x_B-x_A&y_B-y_A\\ 0&x_C-x_A&y_C-y_A \end{vmatrix} = \begin{vmatrix} x_B-x_A&y_B-y_A\\ x_C-x_A&y_C-y_A \end{vmatrix} \\&= (x_B - x_A)(y_C - y_A) - (x_C - x_A)(y_B - y_A) \\ &= \begin{cases} < 0, & \text{wenn }C\text{ ist rechts von }\overrightarrow{AB} \\ = 0, & \text{wenn }C\text{ ist auf }\overrightarrow{AB} \\ > 0, & \text{wenn }C\text{ ist links von }\overrightarrow{AB} \end{cases} \end{align}$

Berechnung

Nach Winkel sortierte Punktmenge – $P_0$ wird als Startpunkt gewählt, da er den kleinsten Ordinatenwert hat. $P_1$ fällt heraus, da er mit $P_2$ und $P_0$ kollinear ist.

$S$ sei nun die sortierte Punktmenge. Als Nächstes läuft man alle Punkte in $S$ durch und prüft, ob diese Eckpunkte der konvexen Hülle sind. Es wird ein Stapelspeicher (Stack) angelegt, auf welchem sich alle Eckpunkte der konvexen Hülle für alle bereits abgearbeiteten Punkte befinden. Zu Beginn liegen $P_0$ und $P_1$ auf dem Stapel. Im $k$-ten Schritt wird $P_k$ zur Betrachtung herangezogen und berechnet, wie er die vorherige konvexe Hülle verändert. Aufgrund der Sortierung liegt $P_k$ immer außerhalb der Hülle der vorherigen Punkte $P_i$ mit $i < k$.

Durch das Hinzufügen des Punktes kann es vorkommen, dass bereits auf dem Stapel liegende Punkte nicht mehr zur neuen konvexen Hülle gehören. Diese Punkte müssen mittels der „pop“ Operation vom Stapel entfernt werden. Ob ein Punkt noch zur konvexen Hülle gehört oder nicht ermittelt man, indem man berechnet, ob $P_k$ links oder rechts des Vektors PT2→PT1 liegt (PT1 = oberstes Element des Stapels, PT2 = Element direkt unter PT1). Liegt $P_k$ links, so bleibt PT1 weiterhin auf dem Stapel und $P_k$ wird mit „push“ auf dem Stapel abgelegt, liegt $P_k$ rechts, so wird PT1 von der neuen konvexen Hülle verschluckt, vom Stapel entfernt und die nächsten beiden oberen Punkte untersucht.

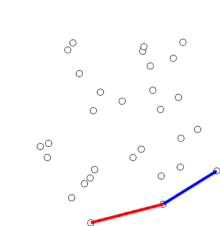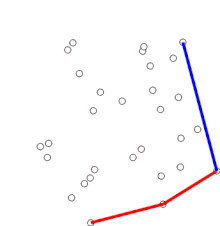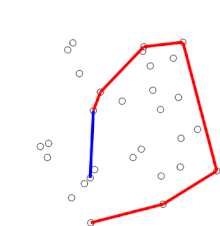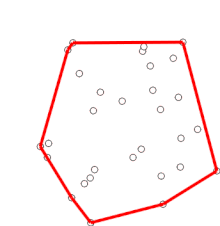
Dieser Test wird solange durchgeführt, bis $P_k$ links des Vektors PT2→PT1 oder nur noch $P_0$ und ein weiterer Punkt auf dem Stapel liegt. In beiden Fällen wird dann $P_k$ auf dem Stapel abgelegt und mit dem nächsten Punkt $P_{k+1}$ weitergerechnet. Die folgende Abbildung zeigt ein Beispiel, in welchem alle Fälle des eben beschriebenen Tests auftreten.

Beispiel – Graham Scan Algorithmus

In nebenstehender Abbildung werden zunächst die Punkte Pt4, Pt3, Pt2 und $P_{k-1}$ auf den Stack gelegt. Zu jedem Zeitpunkt bilden die Punkte auf dem Stack ein konvexes Polygon (gestrichelte Linien). Erst als $P_k$ hinzukommen soll, fallen $P_{k-1}$ und Pt2 wieder raus, da sie zusammen mit $P_k$ nicht konvex sind. Die konvexe Hülle dieser Punktmenge besteht aus $P_0$, Pt4, Pt3 und $P_k$. $P_0$ liegt dabei auf dem Stack ganz unten und $P_k$ ganz oben. Die Punkte des gesuchten konvexen Polygons können mit „pop“ im Uhrzeigersinn vom Stapel geholt werden.

Anmerkung

Die Anzahl der „push“ und „pop“ Operationen übersteigt die obere Grenze von $2N$ ($N$ = Anzahl der Punkte in der Eingabemenge) nicht. Die Berechnung ist also $O(N)$. Die Sortierung der Punkte nach Winkel kann mit jedem beliebigen Sortieralgorithmus durchgeführt werden, z. B. dem Mergesort. Dieser hat eine asympt. Laufzeit von $O(N \log N)$. Das bedeutet, dass die Laufzeit des Algorithmus durch die Sortierung vorgegeben ist, da $O(N) + O(N \log N) = O(N \log N)$.

Pseudocode

Unter Nutzung eines Stacks

Funktion GrahamScan
  Eingabe: Punktemenge S = {P}
  Ausgabe: konvexe Hülle von S
  Beginn Funktion
    Sei S die nach dem Winkel zu P0 sortierte Punktemenge
    PUSH(P0)
    PUSH(P1)
    i := 2
    n := Anzahl der Punkte in S
    
    Solange i < n, führe aus:
      Sei Pt1 der oberste Punkt auf dem Stack
      Sei Pt2 der zweitoberste Punkt auf dem Stack
      Wenn Si links des Vektors Pt2→Pt1 liegt, dann führe aus:
        PUSH(Si)
        i := i + 1
      Ansonsten führe aus:
        POP(Pt1)
      Ende Bedingung
      
    Ende Schleife
    
  Ende Funktion

Ohne Nutzung eines Stacks

Funktion GrahamScan
  Eingabe: Punktemenge S = {P}
  Ausgabe: konvexe Hülle von S
  Beginn Funktion
    Sei S die nach dem Winkel zu P0 sortierte Punktemenge
    i := 1
    
    Solange i+1 < |S|, führe aus:
      Wenn Si rechts des Vektors Si−1→Si+1 liegt, dann führe aus:
        i := i + 1
      Ansonsten führe aus:
        Entferne das Element Si aus S
        i := i - 1
      Ende Bedingung
    
    Ende Schleife
  
  Ende Funktion

Im Code sei punkte ein Array aus Punkten, aus dem man mit punkte[i] das i-te Element erhält und welches schon nach dem Winkel zu punkte[0] sortiert ist. Der Code verändert dieses Array, indem die Elemente gelöscht werden, die nicht zur konvexen Hülle gehören.

Weblinks

• Erklärungen samt Visualisierung des Verfahrens
• Computational Geometry in C (Second Edition)
• Erklärung und Pseudocode