Kakuro

Ein einfaches Kreuzsummenrätsel (Kakuro).

Zugehörige Lösung

Kakuro oder Kakro (japanisch カックロ kakkuro von 加算クロス kasan kurosu, deutsch ‚Summe + Kreuz‘) ist eine Logikrätselgattung.

Im deutschen Sprachraum sind außer Kakuro auch die Namen Kreuzzahlenrätsel, Kreuzsumme und Zahlenschwede in Gebrauch.

Regeln

Der Aufbau ähnelt dem eines Kreuzworträtsels, nur mit Ziffern statt Buchstaben und Summen statt Wortdefinitionen.

Die Zahlen in der oberen Ecke eines Kästchens zeigen an, welche Summe die Zahlen in der Reihe von freien Feldern rechts davon haben sollen, die Zahlen in der unteren Ecke beschreiben auf dieselbe Art die senkrechten Felder direkt darunter.

Dabei gelten folgende Regeln:

• Es dürfen nur die Ziffern von 1 bis 9 vorkommen
• In jeder Summe darf jede Ziffer nur einmal vorkommen
• In jedes freie Feld darf nur eine Ziffer eingetragen werden

Normalerweise wird die Lösung durch die vorgegebenen Zahlen eindeutig festgelegt.

Geschichte

Kakuro ist eines der ältesten Logikrätsel, das auf einem Gitter gespielt wird. Ein Kakuro befindet sich bereits in der April/Mai-Ausgabe der Dell Publishing Company aus dem Jahre 1950 und hat in Japan eine vergleichbare Beliebtheit wie Sudoku.

Darstellungen

Da im Japanischen Wort Kakuro die Wortwurzel kuro (= schwarz) steckt, werden die Summenfelder häufig als schwarze Flächen (mit weißer Schrift) dargestellt. Bis auf die Darstellung der Summenfelder ist die Darstellung eines Kakuros recht einheitlich.

• 
  Traditionelle Form eines kakuro mit schwarzen Summenfeldern
• 
  Kakuro mit weißen Summenfeldern
• 
  Kakuro mit grauen Summenfeldern

Mathematische Überlegungen

Die zu einer Zahl gehörenden freien Felder (rechts von oder unter ihr, je nachdem) heißen im Folgenden „Stellen“ dieser Zahl. Man darf allerdings bei allen Summenüberlegungen nicht vergessen, dass sie nur etwas über die in der Reihe enthaltenen Zahlen aussagen, im Allgemeinen aber nichts über ihre Reihenfolge. Die genaue Reihenfolge muss dann durch weitere logische Schlüsse oder Kombinationen aus Summenüberlegungen erschlossen werden.

Eindeutigkeit von Summen

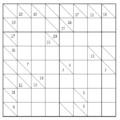
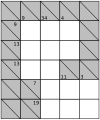
Die einfachste mathematische Überlegung, die man sich beim Lösen von Kakuro zunutze macht, ist folgende: Für eine gegebene Anzahl Stellen (Felder) sind bestimmte Summen eindeutig bestimmt. Betrachtet man beispielsweise die Zahl 7 unten rechts senkrecht in obigem Beispiel: Sie soll mit drei Stellen gebildet werden. Hierfür kommt ausschließlich die Zahlenkombination (1, 2, 4) in einer bisher noch nicht bekannten Reihenfolge in Frage. Die Zahl 6 links unten waagerecht lässt sich nur durch eine Kombination der Zahlen (1, 2, 3) in drei Stellen darstellen.

Folgende Zahlen besitzen nur eine einzige Zerlegung in zwei zulässige Summanden: 3 (1, 2), 4 (1, 3), 16 (7, 9) und 17 (8, 9). Ebenso lassen sich Zahlen finden, die nur eine einzige Zerlegung in noch mehr Summanden zulassen.

Bei 2 bis 9 Feldern existieren 502 Zahlensets, aus denen die Lösungen bestehen können. Bei einigen Felder-Summen-Kombinationen gibt es nur ein Zahlenset, das Maximum von 12 Zahlensets findet man bei der Summe 20 und 4 Feldern sowie bei der Summe 25 und 5 Feldern. Durch die Permutation steigt die Zahl der Möglichkeiten im letzten Fall auf 1440 (12 × 5!). Bei 9 Feldern existiert zwar nur ein Zahlenset – nämlich alle Ziffern von 1–9 gemeinsam –, aber durch die Permutation steigt die Zahl der Möglichkeiten auf 9! = 362880. Bei einigen Felder-Summen-Kombinationen sind manche Ziffern gar nicht enthalten. Bei 6 Feldern und Summe 37 z. B. gibt es 2 Zahlensets, aber keines enthält eine 1. Wenn eine 2 oder eine 5 gesichert ist, kann weder eine 3 noch eine 4 vorkommen. Umgekehrt kann keine 2 und auch keine 5 vorkommen, wenn eine 3 oder eine 4 gesichert ist. Durch Streichen dieser Kandidaten wird die Lösung weiter eingegrenzt.

Mindestsumme und Höchstsumme

Da in den Feldern des Kakuro nur die Ziffern 1 bis 9 eingetragen werden dürfen, hat zu einer gegebenen Anzahl Stellen deren Summe einen Maximalwert. Eine Reihe von vier Feldern hat beispielsweise maximal den Wert $30=9+8+7+6$. Ebenso hat dieselbe Reihe von Feldern minimal den Wert $10=1+2+3+4$.

Formelmäßig lässt sich der Maximal- bzw. Minimalwert einer Summe abhängig von der Stellenanzahl $n$ wie folgt ausdrücken ($u(n)$ bezeichnet den Maximal-, $l(n)$ den Minimalwert):

$u(n)=\sum _{k=9-n+1}^{9}k={\frac {19\cdot n-n^{2}}{2}}$

$l(n)=\sum _{k=1}^{n}k={\frac {n\cdot (n+1)}{2}}$ (Gaußsche Summenformel)

Beschränkungen

Da sich die Ziffern in einer Reihe nicht wiederholen dürfen, hat eine Reihe maximal neun Stellen und damit maximal den Wert 45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.

Lösungsmethoden

Zur Lösung eines Kakuros versucht man nach und nach immer mehr Zahlen in die entsprechenden Felder einzutragen, die sich dann zu immer größeren Bereichen ergänzen.

Einfache Kakuros enthalten Gruppen aus nur einem Quadrat, in denen folglich die Summe mit der Zahl selbst übereinstimmt. Des Weiteren lassen sich oft durch die angegebene Summe die überhaupt noch möglichen Zahlen in den Feldern dieser Summe stark eingrenzen. Wie oben erwähnt ergeben sich manchmal eindeutige Zerlegungen. So kann beispielsweise eine Summe mit zwei Feldern und Summe 3 nur die Zahlen 1 und 2 enthalten, eine mit der Summe 7 ausschließlich die Summanden 1 und 6 oder 2 und 5 oder 3 und 4. Ebenso lassen sich für alle weiteren Summen und auch für größere Bereiche die entsprechenden Kombinationsmöglichkeiten angeben. Manchmal werden auch vollständige Tabellen dieser Summenzerlegungen zur Lösung eines Kakuros verwendet. Im Allgemeinen lassen diese sich aber sehr schnell durch logische Überlegungen finden.

Oftmals können einzelne Zahlen dadurch gefunden werden, dass man die Summenzerlegungen verschiedener Zahlen gleichzeitig betrachtet. So ist im Beispiel links sowohl die Zerlegung der Summe 34 auf 5 Felder (4 + 6 + 7 + 8 + 9) als auch der Summe 7 auf 3 Felder (1 + 2 + 4) eindeutig, so dass für das gemeinsame Feld nur die Zahl 4 übrig bleibt.

Varianten

• Japanische Summen: Hier sind die Positionen der Leerfelder nicht bekannt.
• Killer-Sudoku: Es kombiniert Kakuro mit Sudoku.

Weblinks

Commons: Kakuro – Sammlung von Bildern, Videos und Audiodateien

• Linkkatalog zum Thema Kakuro bei curlie.org (ehemals DMOZ)
• Tabellen möglicher Summen. (PDF; 37,1 KB) In: Kakuro-Knacker. Abgerufen am 13. März 2015. 
• Kakuro Total Tables. In: PuzzleBooks.net. Abgerufen am 13. März 2015 (englisch).