Nachzerfallswärme
Mit Nachzerfallswärme (englisch decay heat) – manchmal auch einfach Nachwärme – bezeichnet man in der Kernreaktor-Technik die Zerfallswärmeleistung, die nach dem Beenden der Kernspaltungsreaktion in den Brennelementen noch neu entsteht.[3] Da der Neutronenfluss z. B. durch Einfahren der Steuerstäbe nahezu zum Erliegen gekommen ist, finden nach der Abschaltung kaum neue Spaltungsreaktionen statt. Die Nachzerfallswärme kommt vielmehr dadurch zustande, dass die vorhandenen, kurzlebigen Spaltprodukte radioaktiv zerfallen. Wärmeleistung durch nachgeordnete Zerfallsprozesse fällt auch im normalen, kontinuierlichen Reaktorbetrieb laufend an; mit Nachzerfallswärme ist aber nur jene Wärme gemeint, die im Abschaltzustand neu entsteht. Derartige Zerfallswärme entsteht auch in gebrauchten Brennelementen im Abklingbecken, in Castoren oder Lagern.
Umgangssprachlich wird die Nachzerfallswärme auch als „Restwärme“ bezeichnet. Diese Bezeichnung ist missverständlich, da sie mit der gespeicherten Wärmemenge im Reaktorkern verwechselt werden kann.
Nachzerfallswärme im Reaktorkern[Bearbeiten | Quelltext bearbeiten]
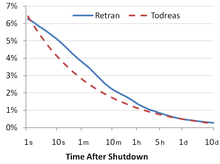
Die Nachzerfallswärmeleistung beträgt unmittelbar nach dem Abschalten zwischen 5 % und 10 % der vorherigen thermischen Leistung des Reaktors, abhängig vom Reaktortyp, der Betriebsdauer und dem eingesetzten Kernbrennstoff. In einem Großreaktor wie beispielsweise dem EPR mit 1600 MW elektrischer Leistung, d. h. rund 4000 MW thermischer Leistung,[Anm. 1] entstehen eine Stunde nach der Abschaltung noch rund 50 MW Wärmeleistung, nach vier Tagen noch 20 MW.[4]
Berechnung[Bearbeiten | Quelltext bearbeiten]
Die verbleibende Menge eines Radionuklids am Anfang der Zerfallskette sinkt zeitlich entsprechend einer Exponentialfunktion. Für Nuklide, die erst gebildet werden, ist der Zeitverlauf eine Summe von auf- und abklingenden Exponentialfunktionen, falls nur Reaktionen erster Ordnung berücksichtigt werden. Neutroneneinfang ist eine Kernreaktion zweiter Ordnung, ist jedoch in Gegenwart von Neutronenabsorbern für den Kernbrennstoff zweitrangig. Beim Spaltproduktgemisch in einem Reaktor überlagern sich die zahlreichen Exponentialfunktionen mit breit verteilten Zeitkonstanten zu einem Verlauf, der für praktische Zwecke z. B. als Potenzfunktion angenähert werden kann. Berechnungsvorschriften sind in den Normen DIN 25463-1 und DIN 25463-2 festgelegt.
Eine einfache Näherungsformel wurde 1946 von Katharine Way und Eugene Wigner angegeben:[5][6] Wird ein Reaktor für die Dauer mit der Leistung betrieben, so sei die Nachzerfallsleistung zum Zeitpunkt nach dem Abschalten des Reaktors
Dabei sind T0 und t in Sekunden einzusetzen. Für die Gültigkeit wurde der Zeitbereich von 10 Sekunden bis 100 Tagen angegeben, die Unsicherheit mit 15 % bis 20 %.
Die Herleitung haben Way und Wigner ausführlich dargestellt. Die Annahmen und Näherungen in Kürze:
- Die Massenzahlen und der Spaltprodukte wurden bei den Maxima der beobachteten Verteilungen fixiert.
- Für die leichten (L) und schweren (H) Spaltprodukte wurde jeweils die Verteilung der Protonenzahl als Gauß-Verteilung genähert.
- Die die Kinetik bestimmenden Lebensdauern der -Strahler wurde nach der Sargent-Regel umgekehrt proportional zur fünften Potenz der Energiedifferenz von Mutter- und Tochterkern gesetzt, die wiederum mit der Bethe-Weizsäcker-Formel berechnet wurde.
Für die mittlere Nachzerfallsleistung der Produkte eines einzelnen auslösenden Spaltereignisses ergibt sich ein Abklingen proportional zu , wenn das auslösende Spaltereignis zur Zeit stattfand, bzw.
für einen allgemeinen Startzeitpunkt .
Unter der Annahme, dass Kerne gleichverteilt über ein Intervall gespalten wurden, erhält man die gesamte Nachzerfallsleistung durch Integration über die verschiedenen Startzeitpunkte :
Die Anzahl der gespaltenen Kerne pro Sekunde kann mit der (als zeitlich konstant angenommenen) Leistung des Reaktors in Verbindung gesetzt werden:
Dabei ist die mittlere Energie, die pro Spaltung thermisch nutzbar ist (etwa 200 MeV pro Spaltung). Daher kann man die Nachzerfallsleistung auch auf die gefahrene Reaktorleistung beziehen, wie oben angegeben. Der korrekte Vorfaktor ergibt sich demnach aus der korrekten mittleren Einzelnachzerfallsleistung und der mittleren, pro Spaltung thermisch nutzbaren Energie.
Beispiele für Nachzerfallswärme nach langer Betriebsdauer[Bearbeiten | Quelltext bearbeiten]
Nach 11 Monaten Betrieb nahe der Nennleistung in einem typischen Brennelementzyklus ergeben sich aus der obigen Formel folgende Werte (Leistungswerte und Zeitdauern sind auf den Brennstoffinhalt eines typischen Großreaktors bezogen):
| Zeit nach Abschal- tung |
Nach- zerfalls- Wärme |
Thermische Leistung bei 4000 MW vor Abschaltung |
Dauer um 2500 m³ Wasser von 15 auf 100 °C zu erwärmen[Anm. 2] |
|---|---|---|---|
| 10 sec | 3,72 % | 149 MW | 100 min |
| 1 min | 2,54 % | 102 MW | 146 min |
| 1 h | 1,01 % | 40 MW | 6 h |
| 1 Tag | 0,44 % | 18 MW | 14 h |
| 3 Tage | 0,31 % | 13 MW | 20 h |
| 1 Woche | 0,23 % | 9 MW | 26 h |
| 1 Monat | 0,13 % | 5 MW | 49 h |
| 3 Monate | 0,07 % | 3 MW | 89 h |
Nachzerfallswärme im Abklingbecken[Bearbeiten | Quelltext bearbeiten]
Ungekühlt würden verbrauchte („abgebrannte“) Brennelemente sich nach Entladung aus dem Reaktorkern noch mehrere Monate nach Ende des Betriebs bis zum Schmelzpunkt erhitzen. Um ihre Nachzerfallswärme abzuführen, müssen diese Brennelemente mehrere Jahre lang in den zu jedem Kernkraftwerk gehörenden wassergefüllten Abklingbecken gelagert werden. Die Wärmeleistung aus den Abklingbecken wird aktiv abgeführt; in neueren Anlagen wird sie wirtschaftlich genutzt, um das Reaktor-Speisewasser vorzuwärmen (Abklingbecken-Speisewasservorwärmer-Kühlkreislauf). Im Jahr 2021 schlug eine Arbeit der TU Prag und der Universität Plzeň die Nutzung der Nachzerfallswärme für Fernwärme vor.[7]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Auslegungsstörfall
- Dampfblasenkoeffizient
- Kühlmittelverluststörfall
- Liste von Unfällen in kerntechnischen Anlagen
- Sicherheit von Kernkraftwerken
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ RETRAN-02. Nuclear Power Industry Engineering & Consulting. CSA, abgerufen am 27. März 2011 (englisch).
- ↑ Neil E. Todreas, Mujid S. Kazimi: Nuclear Systems I, Thermal Hydraulic Fundamentals. 2. Auflage. Hemisphere Publishing Corporation, New York 1990, ISBN 0-89116-935-0.
- ↑ Kernspaltung und Nachzerfallswärme. Gesellschaft für Anlagen- und Reaktorsicherheit, 22. März 2011, abgerufen am 28. November 2013.
- ↑ R. Zahoransky (Hrsg.): Energietechnik. 5. Auflage. Vieweg und Teubner, 2010, ISBN 978-3-8348-1207-0, Seite 81
- ↑ Katharine Way, Eugene P. Wigner: Radiation from Fission Products. Technical Information Division, United States Atomic Energy Commission, Oak Ridge (Tennessee) 1946.
- ↑ K. Way, E. P. Wigner: The Rate of Decay of Fission Products. In: Physical Review. Band 73, 1948, S. 1318–1330.
- ↑ Lubos Palata: Nuclear heating: A low-cost, greener option? In: dw.com. 7. April 2021, abgerufen am 18. Februar 2024 (englisch).
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Der Wirkungsgrad des Reaktors entspräche dementsprechend rund 30 %, siehe auch Wirkungsgrad-Beispiele
- ↑ Inhalt eines olympischen Schwimmbeckens














![{\displaystyle [-T_{0},0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7d10b9aad9fe820d9c240263977ad78a3626ad)


