RC6
| RC6 | |
|---|---|
| Entwickler | Ronald L. Rivest, Matt Robshaw, Ray Sidney, Yiqun Lisa Yin |
| Veröffentlicht | 1997 |
| Abgeleitet von | RC5 |
| Schlüssellänge | 128, 192 oder 256 Bit |
| Blockgröße | 128 Bit |
| Struktur | Feistelchiffre |
| Runden | 20 |
RC6 (Rivest Cipher 6) ist eine 1998 von Ronald Rivest und anderen entworfene symmetrische Blockverschlüsselung. RC6 ist eine Weiterentwicklung von RC5 und verwendet ebenso wie dieses datenabhängige Rotationen, und zusätzlich die Multiplikation von Daten. Die zum Entwicklungszeitpunkt bekannten theoretischen Angriffe gegen RC5 sollten dadurch bereits im Ansatz verhindert werden.[1]
RC6 kandidierte zur Wahl des Advanced Encryption Standards (AES) und zählte dort – zusammen mit Twofish, Rijndael, MARS und Serpent – zu den Finalisten. Es wurde vom National Institute of Standards and Technology (NIST) als „hinreichend sicher“ eingestuft – ebenso wie Rijndael, welches schließlich zum AES gewählt wurde. RC6 ist einfacher aufgebaut als die anderen Finalisten, wodurch die Gefahr von Implementierungsfehlern reduziert wird, und es ist auch relativ effizient in Software zu implementieren.
Beschreibung[Bearbeiten | Quelltext bearbeiten]
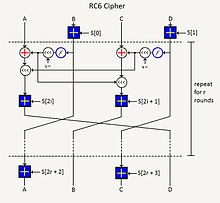
RC6 besitzt variable Blockgrößen, Rundenzahlen (0–255) und Schlüssellängen (0–2040 Bit). Eine spezifische Wahl dieser Parameter wird üblicherweise mit „RC6-w/r/b“ bezeichnet – w ist die Länge eines Datenworts in Bit, r die Anzahl der Runden und b die Länge des Schlüssels. Ein Block besteht immer aus vier Datenwörtern, die Blockgröße ist also Bit. Der AES-Kandidat war RC6-32/20 mit Blockgröße 128 Bit, 20 Runden und Schlüssellängen von 128, 192 und 256 Bit.[1]
Als Primitive Operationen verwendet der Algorithmus die Addition () und Multiplikation () (jeweils modulo ), die bitweise XOR-Verknüpfung () und die Linksrotation (), die um Bitpositionen rotiert.[1]
Ver- und Entschlüsselung[Bearbeiten | Quelltext bearbeiten]
Gegeben seien ein Klartextblock in Little-Endian-Darstellung, der aus den Datenworten A, B, C, D besteht, und die Rundenschlüssel S0 bis S2r+3. Dabei bezeichnet den Logarithmus der Wortlänge zur Basis 2. Der Block wird verschlüsselt durch:
Wie bei RC5 werden S0 und S1 zum Key Whitening verwendet.
Die Entschlüsselung eines Chiffretextblocks entspricht der Umkehrung dieses Algorithmus.[1]
Schlüsselexpansion[Bearbeiten | Quelltext bearbeiten]
| Blockgröße [Bits] |
P [hexadezimal] |
Q [hexadezimal] |
|---|---|---|
| 64 | B7E1 | 9E37 |
| 128 | B7E1 5163 | 9E37 79B9 |
| 256 | B7E1 5162 8AED 2A6B | 9E37 79B9 7F4A 7C15 |
Der Expansionsalgorithmus von RC6, der die Rundenschlüssel S0 bis S2r+3 berechnet, wurde im Wesentlichen unverändert von RC5 übernommen. Zunächst werden die Rundenschlüssel Sk mittels Konstanten auf einen festen Anfangszustand initialisiert. P und Q sind – wie bei RC5 – ungerade Ganzzahlen, die mit der eulerschen Zahl e und dem goldenen Schnitt Φ in Abhängigkeit von der verwendeten Blockgröße generiert werden (Tabelle).
Anschließend wird der geheime Schlüssel in c Wörter bis der Länge w aufgespalten, und bei Bedarf wird das letzte Wort mit Nullen aufgefüllt. Folgender Code berechnet dann die endgültigen Rundenschlüssel:
Kryptoanalyse[Bearbeiten | Quelltext bearbeiten]
Chosen-Plaintext[Bearbeiten | Quelltext bearbeiten]
2001 wiesen Tetsu Iwata und Kaoru Kurosawa des Tokyo Institute of Technology nach, dass ein idealisiertes RC6 mit 4 Runden keine pseudozufällige Permutation darstellt – ein Angreifer mit polynomiell vielen Verschlüsselungsversuchen das Ergebnis der Blockchiffre also von zufälligem Rauschen unterscheiden kann.[2] Im gleichen Jahr stellten Henri Gilbert, Helena Handschuh, Antoine Joux und Serge Vaudenay einen auf dieser Eigenschaft aufbauenden statistischen Angriff vor, mit dessen Hilfe sich – für w = 32 – mit 2118 Paaren aus gewählten Klartexten und ihren Chiffraten Bits der Rundenschlüssel für bis zu 13 Runden rekonstruieren lassen. Mit einem Speicherbedarf von 2112 und etwa 2122 notwendigen Operationen kann dieser Angriff zudem auch als Known-Plaintext-Angriff gegen 14 Runden verwendet werden. Aus diesem – aufgrund der Anforderungen praktisch nicht durchführbaren – Angriff schlossen die Autoren, dass die 20 Runden des AES-Kandidaten nicht übermäßig viel seien.[3]
Known-Plaintext[Bearbeiten | Quelltext bearbeiten]
1999 stellten Borst, Preneel und Vandevalle fest, dass der von ihnen publizierte, auf linearen Approximationen basierende Angriff auf RC5 gegen RC6 essentiell wirkungslos ist und die Vorkehrungen der RC6-Entwickler ausreichten.[4]
Lizenzierung[Bearbeiten | Quelltext bearbeiten]
Für das RC6-Verfahren erhielt das Unternehmen RSA die US-Patente 5724428 und 5835600 zugesprochen. Diese liefen allerdings zwischen 2015 und 2017 aus.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Beschreibung von Markus Repges
- NIST, Report on the Development of the Advanced Encryption Standard (AES), 17. Februar 2024
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c d e Ronald L. Rivest, M. J. B. Robshaw, R. Sidney, Y.L. Yin: The RC6 Block Cipher. 1998 (psu.edu).
- ↑ Tetsu Iwata, Kaoru Kurosawa: On the Pseudorandomness of the AES Finalists - RC6 and Serpent. In: Lecture Notes in Computer Science. Band 1978/2001. Springer Berlin / Heidelberg, S. 231.
- ↑ Henri Gilbert, Helena Handschuh, Antoine Joux, Serge Vaudenay: A Statistical Attack on RC6. In: Lecture Notes in Computer Science. Band 1978/2001. Springer Berlin / Heidelberg, S. 1–15.
- ↑ Johan Borst, Bart Preneel, Joos Vandewalle: Linear Cryptanalysis of RC5 and RC6. In: Lecture Notes in Computer Science. Band 1636, Nr. 1999. Springer Berlin / Heidelberg, ISSN 1611-3349, S. 16.

































