Spirograph (Spielzeug)




Spirograph ist ein geometrisches Spielzeug, mit dem man verschiedene Muster oder mathematische Kurven zeichnen kann.
Funktionsweise[Bearbeiten | Quelltext bearbeiten]
Der Spirograph besteht aus mehreren, meist runden, dünnen Zahnrädern aus Plastikscheiben. Zunächst wird ein Blatt Papier auf eine Pappe gelegt. Dann wird, je nach Ausführung, ein größerer verzahnter Plastikring oder eine innenverzahnte Lochschablone darauf (im Original mit Nadeln) befestigt. Im Inneren (oder auch am Äußeren) des Zahnkranzes wird eines der Zahnräder angelegt. Durch die Zähne greifen diese wie bei einer Zahnstange ineinander. In den Zahnrädern befinden sich in verschiedenen Abständen Löcher, durch die die Spitze eines Schreibgerätes gesteckt wird. Hier muss man z. B. mit einem Kugelschreiber in der Zahnscheibe einen Kreis beschreiben.
Durch die Verwendung mehrerer farbiger Kugelschreiber oder Stifte in unterschiedlichen Löchern erhält man verschiedene geometrische Figuren, sogenannte Hypozykloiden und Epizykloiden.
Der Erfinder war 1965 Denys Fisher, der das Spielzeug erstmals auf der Nürnberger Spielwarenmesse vorführte. Es gibt viele verschiedene Versionen, auch mit einem Motor. Der Spirograph war Gewinner des Toy of the Year Award des Jahres 1967.
Doch bereits vor Denys Fisher gab es mindestens zwei Erfinder, die sich Spiralenzeichner patentieren ließen: Bruno Abdank-Abakanowicz[1][2] im Jahre 1885, sowie Ernst Barthel[3] im Jahre 1933.
Mathematische Beschreibung[Bearbeiten | Quelltext bearbeiten]
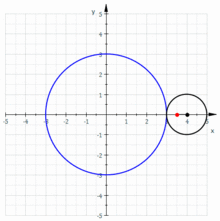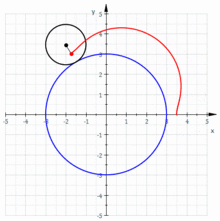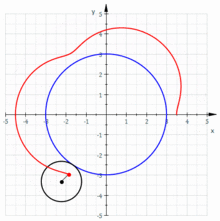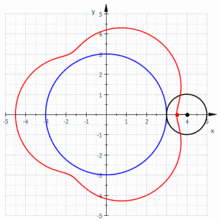
Die Hypotrochoide entsteht, wenn ein kleiner Kreis im Inneren eines großen Kreises abgerollt wird und die Epitrochoide, wenn ein kleiner Kreis im Äußeren eines großen Kreises abgerollt wird. Die nebenstehenden Animationen verdeutlichen dies. Mit den nachfolgend aufgelisteten Parametern lässt sich die Parametrisierung von Epi- und Hypotrochoide wie folgt angeben:
- : Radius des feststehenden Kreises (Innenverzahnte Lochschablone bei Hypo- und außenverzahnte Epitrochoide)
- : Radius des bewegten Kreises (Zahnrad)
- : Radius der Stift-Position bezüglich des Zahnradmittelpunktes
- : Auswahl-Parameter
Wird der Parameter gewählt, so werden die Kurven als Epi- bzw. Hypozykloide bezeichnet. Diese stellen sozusagen einen Spezialfall der Epi- und Hypotrochoide dar. Beim klassischen Spriograph-Spielzeug ist eine solche Konfiguration jedoch nicht möglich. Der Stift befindet sich hier stets in einer Position .
Die nachfolgende Darstellung dient mit zur Beschreibung von periodischen Figuren. Sind und teilerfremd, so steht für die Anzahl der Umläufe des Zahnrades, bis die Kurve geschlossen ist. Die gemeinsame Periodendauer bezüglich des Parameter ist folglich .
Spezielle Hypotrochoiden (), welche durch den Mittelpunkt des Kreises mit Radius verlaufen, ergeben sich durch die Wahl von . In diesem Fall gilt weiterhin das Verhältnis . Bei der in der nebenstehenden Animation dargestellten Hypotrochoide ist dies der Fall. Wird hingegen gewählt, so ergeben sich sternförmige Kurven, deren Spitzen auf dem Kreis mit Radius liegen. Weiterhin ergibt sich in diesem Fall die Anzahl der Stern-Spitzen zu und es gilt das Verhältnis .
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Bruno Abdank-Abakanowicz: Les Intégraphes la Courbe Integrale et ses Applications. Paris: Gauthier-Villars (1. Januar 1886)[4]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Private Webseite mit Beispielen und Formeln
- the journal of antiques: Spirograph
- Retro collectibles Spirograph
- Spirograph History (englisch)
- Virtueller Spirograph von Nathan Friend
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Spiralenzeichner (bei Reunion) ( des vom 14. September 2010 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ Der Spiralzeichner von 1885 im Bild ( des vom 28. September 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis..
- ↑ VDI-Nachrichten, 19. April 1933, Beschreibung des Patents zu Ernst Barthels Transformationszirkel.
- ↑ Frz. Seite ( des vom 7. März 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis..


















